 Haga clic o toque los circuitos de ejemplo a continuación para invocar TINACloud y seleccione el modo DC interactivo para analizarlos en línea.
Haga clic o toque los circuitos de ejemplo a continuación para invocar TINACloud y seleccione el modo DC interactivo para analizarlos en línea. Obtenga un acceso de bajo costo a TINACloud para editar los ejemplos o crear sus propios circuitos
En este y los siguientes capítulos, presentaremos un tema muy importante: CA o corriente alterna. El nombre de corriente alterna no es muy preciso y normalmente cubre circuitos con voltajes y corrientes sinusoidales; sin embargo, la corriente alterna también puede significar cualquier forma de onda de corriente arbitraria. La importancia del voltaje de CA es que este tipo de voltaje se usa para la fuente de energía eléctrica principal en hogares e industrias en todo el mundo. También es la base de muchas aplicaciones electrónicas, de telecomunicaciones e industriales.
Para manejar las formas de onda sinusoidales y los circuitos asociados con ellos, utilizaremos un método simple y elegante llamado método de fasores. Los fasores se basan en las propiedades de los números complejos, que son ideales para representar cantidades sinusoidales. En este capítulo, resumiremos los hechos principales sobre los números complejos y sus operaciones. También mostraremos cómo el Intérprete de TINA facilita los cálculos con números complejos.
Los números complejos constan de dos partes, una parte real (x), que es un número real, y un llamado parte imaginaria (y), que es un número real multiplicado por 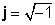
z = x + jy
donde 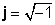
Ejemplos de números complejos:
z 1 = 1 + j
z 2 = 4-2 j
z 3 = 3- 5j
Los números complejos se introdujeron originalmente en el siglo XVII para representar las raíces de polinomios que no podían representarse solo con números reales. Por ejemplo, las raíces de la ecuación x2 + 2x + 2 = 0 solo se puede describir como 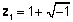
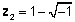
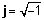
Representación geométrica de números complejos.
Forma rectangular
Debido a que un número complejo siempre se puede separar en sus partes reales y complejas, podemos representar un número complejo como un punto en un plano bidimensional. La parte real de un número complejo es la proyección del punto sobre el eje real, y la parte imaginaria del número es la proyección sobre el eje imaginario. Cuando un número complejo se representa como la suma de partes reales e imaginarias, decimos que está en rectangular or forma algebraica.
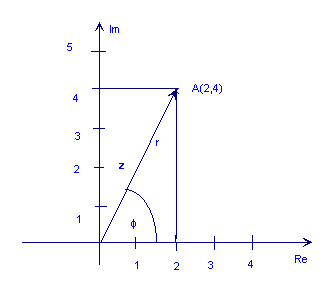
La siguiente figura muestra el número complejo z = 2 + 4j
Forma polar y exponencial.
Como puede ver en la figura anterior, el punto A también podría estar representado por la longitud de la flecha, r (también llamado valor absoluto, magnitud o amplitud) y su ángulo (o fase), φ relativo en sentido antihorario al eje horizontal positivo. Este es el polar forma de un número complejo. Se denota como r ∠ φ.
El siguiente paso es muy importante. Un número complejo en forma polar también se puede escribir en exponencial formar:
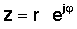
Esta expresión simple es distintiva porque tiene un número imaginario en el exponente en lugar del número real habitual. Este exponencial complejo se comporta de manera muy diferente a la función exponencial con un argumento real. Mientras ex crece rápidamente en magnitud para aumentar x> 0 y disminuye para x <0, la función 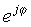
La fórmula de Euler proporciona un enlace unificador entre las formas rectangular, polar y exponencial de los números complejos:
z = x + jy = re jφ = r (cos φ + j el pecado φ )
donde 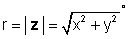
y φ = bronceado-1 (y / x).
Para nuestro ejemplo anterior, z = 2 + 4j:
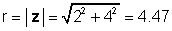
φ = bronceado-1 (4 / 2) = 63.4 °
por lo tanto 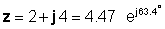
O viceversa:
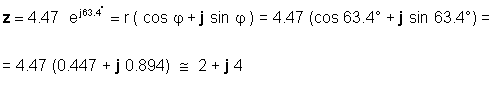
Deberá ser experto en el uso de ambos formularios, dependiendo de la aplicación. Por ejemplo, la suma o la resta son obviamente más fáciles de hacer cuando los números están en forma rectangular, mientras que la multiplicación y la división son más fáciles de hacer cuando los números están en forma exponencial.
Operaciones con números complejos.
Las operaciones que se pueden hacer con números complejos son similares a las de los números reales. Las reglas y algunas definiciones nuevas se resumen a continuación.
Operaciones con j
Las operaciones con j simplemente seguir de la definición de la unidad imaginaria,


Para poder trabajar de forma rápida y precisa, debe memorizar estas reglas:
j 2 = -1
j 3 =-j
j 4 =1
1/j = -j
j2 = -1 simplemente sigue de la definición de 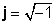
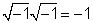
Para 1 /j, multiplicamos 1 /jby j / j = 1 y obtener j/ (jj) = j / (- 1) = -j.
Complejo conjugado
El complejo conjugado de un número complejo se deriva fácilmente y es bastante importante. Para obtener el complejo conjugado de un número complejo en forma rectangular, simplemente cambie el signo de la parte imaginaria. Para hacerlo con un número en forma exponencial, cambie el signo del ángulo del número complejo mientras mantiene su valor absoluto igual.
El complejo conjugado de un número complejo. z a menudo se denota por z*.
Dado el número complejo z= a + jb, su complejo conjugado es z*= a– jb.
If z se da en forma exponencial, 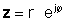
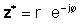
Usando las definiciones anteriores, es fácil ver que un número complejo multiplicado por su conjugado complejo da el cuadrado del valor absoluto del número complejo:
zz* = r2 = Un2 + b2
Además, al sumar o restar cualquier número complejo y su conjugado, obtenemos las siguientes relaciones:
z + z * = 2a
por lo tanto
Re (z) = a = ( z + z * ) / 2
Similar:
z – z * =j2b
por lo tanto
Soy(z) = b = ( z –z * ) / 2j
Prueba:
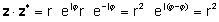
o multiplicando las partes reales e imaginarias y usando j2= -1
zz* = (a + jb) (a - jb) = a2+a jb - a jb - jbjb = a2j2 = a2 + b2
z + z* = a + jb + a - jb = 2a
z - z*= a + jb - a + jb =j2b
Ejemplos numericos:
En forma rectangular:
z = 3 + j4
z* = 3– j4
zz * = 9 + 16 = 25
En forma polar
z = 5 ∠ 53.13 °
z * = 5 ∠- 53.13 °
En forma exponencial:
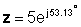
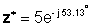
Adición y sustracción
La suma y resta de números complejos es sencilla: solo necesitamos sumar las partes real e imaginaria por separado. Por ejemplo, si
z1 = 3 - 4j y z2 = 2 + 3j
luego
z1 + z2 = 3 - 4j + 2 + 3j = 3 + 2 - 4j + 3j = 5 - j
z1 – z2 = 3 - 4j - 2 - 3j = 3 - 2 - 4j 3 Mayoj = 1 - j7
Obviamente, debemos usar la forma rectangular para estas operaciones. Si los números se dan en forma exponencial o polar, debemos transformarlos primero en forma rectangular usando la fórmula de Euler, como se indicó anteriormente.
Multiplicación
Hay dos métodos para la multiplicación de números complejos:
Multiplicación de números complejos dados en forma rectangular.
Para llevar a cabo la operación, simplemente multiplique las partes real e imaginaria de un número a su vez por las partes real e imaginaria del otro número y use la identidad j2 = -1.
z1z2 = (a1 + jb1) (una2 + jb2) = a1 a2 + jb1a2+ jb2a1 - b1b2 = Un1 a2- b1b2 + j(b1a2+ jb2a1)
Cuando los números complejos se dan numéricamente, no es necesario usar la fórmula anterior. Por ejemplo, vamos
z1 = 3 - 4j y z2 = 2 + 3j
Con multiplicación directa de los componentes:
z1z2 = (3 - 4j) (2 + 3j) = 6- 8j +9j + 12 = 18 + j
o utilizando la fórmula: z1z2 = Un1 a2- b1b2 + j(b1a2+ B2a1)
z1z2 = 6 + 12 + j (-8 + 9) = 18 + j
Creemos que es más probable que cometa un error si usa la fórmula que si multiplica los componentes directamente.
z1: = 3-4 * j
z2: = 2 + 3 * j
z1 * z2 = [18 + 1 * j]
importar matemáticas como m
importar cmath como c
z1=complejo('3-4j')
z2=complejo('2+3j')
imprimir(“z1*z2=”,z1*z2)
Multiplicación de números complejos dados en forma polar o exponencial.
Para llevar a cabo esta operación, multiplique los valores absolutos y agregue los ángulos de los dos números complejos. Dejar:
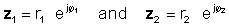
Luego usando la regla de multiplicación de funciones exponenciales:
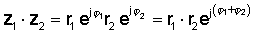
o en forma polar
z1 z2 = r1 r2 ∠ φ1 + φ2
Nota: Ya hemos usado esta regla cuando calculamos zz *encima. Como el ángulo del conjugado tiene el signo opuesto del ángulo original, un número complejo multiplicado por su propio conjugado es siempre un número real; a saber, el cuadrado de su valor absoluto: zz * = r2
Por ejemplo, vamos a:
z1 = 5 ∠ 30 ° y z2 = 4 ∠ -60 °
luego
z1z2 = 20 ∠ -30 °
o en forma exponencial
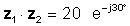
La multiplicación es obviamente más simple cuando los números están en forma polar o exponencial.
Sin embargo, si los números complejos se dan en forma rectangular, debe considerar realizar la multiplicación directamente como se muestra arriba, ya que hay pasos adicionales si convierte los números a forma polar antes de multiplicarlos. Otro factor a considerar es si desea que las respuestas estén en forma rectangular o en forma polar / exponencial. Por ejemplo, si los dos números están en forma rectangular pero desea que su producto esté en forma polar, tiene sentido convertirlos de inmediato y luego multiplicarlos.
División
Hay dos métodos para la división de números complejos:
División de números complejos dados en forma rectangular.
Para llevar a cabo la operación, multiplique el numerador y el denominador por el conjugado del denominador. El denominador se convierte en un número real y la división se reduce a la multiplicación de dos números complejos y una división por un número real, el cuadrado del valor absoluto del denominador.
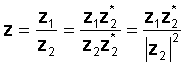
Por ejemplo, dejar:
z1 = 3 - 4j y z2 = 2 + 3j
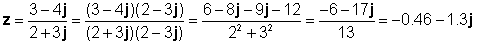
Veamos este resultado con el intérprete de TINA:
z1: = 3-4 * j
z2: = 2 + 3 * j
z1 / z2 = [- 461.5385m-1.3077 * j]
importar matemáticas como m
importar cmath como c
z1=complejo('3-4j')
z2=complejo('2+3j')
imprimir(“z1/z2=”,z1/z2)
División de números complejos dados en forma polar o exponencial.
Para llevar a cabo la operación, divida los valores absolutos (magnitudes) y reste el ángulo del denominador del ángulo del numerador. Dejar:
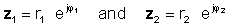
entonces usando la regla de división de funciones exponenciales
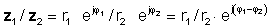
o en forma polar
z 1 / z2 = r1 / r2 ∠ φ 1– φ 2
Por ejemplo, vamos a:
z 1 = 5 ∠ 30 ° y z 2 = 2 ∠ -60 °
luego
z 1 / z2 = 2.5 ∠ 90 °
o en formas exponenciales y rectangulares.
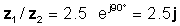
Veamos este resultado con el intérprete de TINA:
z1: = 5 * exp (j * degtorad (30))
z2: = 2 * exp (j * degtorad (-60))
z1 / z2 = [0 + 2.5 * j]
importar matemáticas como m
importar cmath como c
z1=5*(c.exp(complejo(0,m.radianes(30))))
z2=2*(c.exp(complejo(0,m.radianes(-60))))
imprimir(“z1/z2=”,z1/z2)
La división es obviamente más simple cuando los números están en forma polar o exponencial.
Sin embargo, si los números complejos se dan en forma rectangular, debe considerar realizar la división directamente usando el método conjugado complejo como se muestra arriba, ya que hay pasos adicionales si convierte los números a forma polar antes de dividirlos. Otro factor a considerar es si desea que las respuestas estén en forma rectangular o en forma polar / exponencial. Por ejemplo, si los dos números están en forma rectangular, pero desea su cociente en forma polar, tiene sentido convertirlos de inmediato y luego dividirlos.
Ahora vamos a ilustrar el uso de números complejos por problemas más numéricos. Como de costumbre, verificaremos nuestras soluciones usando el intérprete de TINA. El intérprete trabaja con radianes, pero tiene funciones estándar para la conversión de radianes a grados o viceversa.
ejemplo 1 Encuentra la representación polar:
z = 12 - j 48
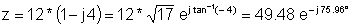
z: = 12-j * 48;
abs (z) = [49.4773]
arco (z) = [- 1.3258]
radtodeg (arco (z)) = [- 75.9638]
importar matemáticas como m
importar cmath como c
z=12-complejo(48j)
imprimir(“abs(z)=”,abs(z))
imprimir(“arco(z)=”,c.fase(z))
print(“grados(arco(z))=”,m.grados(c.fase(z)))
ejemplo 2 Encuentra la representación rectangular:
z = 25 e j 125 °
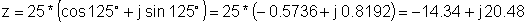
z: = 25 * exp (j * (degtorad (125)));
z = [- 14.3394 + 20.4788 * j]
Re (z) = [- 14.3394]
Im (z) = [20.4788]
importar matemáticas como m
importar cmath como c
z=25*c.exp(complejo(0,m.radianes(125)))
imprimir(“z=”,z)
imprimir(“real(z)=”,z.real)
imprimir(“imag(z)=”,z.imag)
ejemplo 3 Encuentra la representación polar de los siguientes números complejos:
z 1 = 12 + j 48 z2 = 12 - j48 z3= -12 + j 48 z4= -12 - j 48
Los valores absolutos de los cuatro números son los mismos porque el valor absoluto es independiente de los signos. Solo los ángulos son diferentes.
z1: = 12 + j * 48;
abs (z1) = [49.4773]
arco (z1) = [1.3258]
radtodeg (arc (z1)) = [75.9638]
z2: = 12-j * 48;
abs (z2) = [49.4773]
arco (z2) = [- 1.3258]
radtodeg (arc (z2)) = [- 75.9638]
z3: = - 12 + j * 48;
abs (z3) = [49.4773]
arco (z3) = [1.8158]
radtodeg (arc (z3)) = [104.0362]
z4: = - 12-j * 48:
abs (z4) = [49.4773]
arco (z4) = [- 1.8158]
radtodeg (arc (z4)) = [- 104.0362]
importar matemáticas como m
importar cmath como c
z1=complejo('12+48j')
imprimir(“abs(z1)=”,abs(z1))
imprimir(“arco(z1)=”,c.fase(z1))
print(“grados(arco(z1))=”,m.grados(c.fase(z1)))
z2=complejo('12-48j')
imprimir(“abs(z2)=”,abs(z2))
imprimir(“arco(z2)=”,c.fase(z2))
print(“grados(arco(z2))=”,m.grados(c.fase(z2)))
z3=complejo('-12+48j')
imprimir(“abs(z3)=”,abs(z3))
imprimir(“arco(z3)=”,c.fase(z3))
print(“grados(arco(z3))=”,m.grados(c.fase(z3)))
z4=complejo('-12-48j')
imprimir(“abs(z4)=”,abs(z4))
imprimir(“arco(z4)=”,c.fase(z4))
print(“grados(arco(z4))=”,m.grados(c.fase(z4)))
La función arc () de TINA determina el ángulo de cualquier número complejo, colocándolo automáticamente en uno de los cuatro cuadrantes.
Ten cuidado, sin embargo, usando el bronceado-1 función para encontrar el ángulo, ya que está restringido a devolver ángulos solo en el primer y cuarto cuadrantes (–90 °φ<90 °).
Como z1 Está ubicado en el primer cuadrante del sistema de coordenadas, el cálculo es:
α 1 = bronceado-1(48 / 12) = bronceado-1(4) = 75.96 °
Como z4 Está ubicado en el tercer cuadrante del sistema de coordenadas, tan-1No devuelve el ángulo correctamente. El cálculo del ángulo es:
α 4 = 180 ° + 75.96 ° = 255.96 ° o -360 ° + 255.96 ° = - 104.04 °, que es lo mismo calculado por TINA.
z2 está ubicado en el cuarto cuadrante del sistema de coordenadas. El cálculo del ángulo es:
α 2 = bronceado-1(-48 / 12) = bronceado-1(-4) = -75.96 °
z3, sin embargo, está en el cuadrante 2nd del sistema de coordenadas, así que tan-1 No devuelve el ángulo correctamente. El cálculo del ángulo es:
α 3 = 180 ° -75.96 ° = 104.04 °.
ejemplo 4 Tenemos dos números complejos: z1= 4 - j 6 y z2 = 5 ej45 ° .
Encuentre z3 = z1 + z2; z4 = z1 – z2; z5 = z1 * z2; z6 = z1 / z2
Primero resolvemos el problema usando el intérprete de TINA
{Solución del intérprete de TINA} |
Observe cómo TINA maneja sin esfuerzo los dos números complejos dados en diferentes formas.
La solución es más complicada sin el intérprete. Para poder comparar los diferentes métodos de multiplicación y división, primero determinaremos la forma polar de z1 y la forma rectangular de z2 .
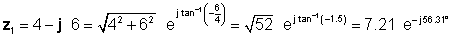
A continuación, encontramos las cuatro soluciones usando primero las formas más fáciles: rectangular para suma y resta, y exponencial para multiplicación y división:
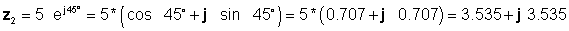
z 3 = z1 + z2 = 4 - j 6 + 3.535 + j 3.535 = 7.535 - j2.465
z 4 = z1 – z2 = 4 - j 6 - 3.535 - j 3.535 = 0.465 - j9.535
z 5 = z1 * z2 = 7.21 * 5 * ej(-56.31 ° + 45 °) = 36.05 e –j11.31 ° = 36.03 * (cos (-11.31 °) +j* sin (-11.31 °))
z 5 = 35.33 - j 7.07
z 6 = z1/z2= (7.21 / 5) * e j (-56.31 ° -45 °) = 1.442 e – j 101.31 ° = 1.442 (cos (-101.31 °) +j* sin (-101.31 °))
z 6 = -0.2828 - j 1.414
Los cuales concuerdan con los resultados obtenidos con el intérprete TINA.
La multiplicación efectuada en forma rectangular:
z 5 =z1*z2 = (4-j6) * 3.535 * (1 +j) = 7.07 * (2-j3) * (1 +j) = 7.07 * (2-j3+j2 + 3) = 7.07 * (5-j) = 35.35-j7.07
Finalmente la división se llevó a cabo en forma rectangular:
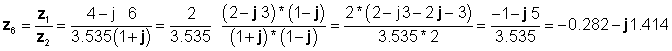
Que coinciden con los resultados anteriores.

