10. עיצוב מגבר FET
עיצוב מגבר FET
כעת אנו חוקרים את הרחבת ניתוח מגבר FET שהוצג קודם לכן בפרק זה לתכנון מגברי FET. ננסה להגדיר את הבלתי ידועים בבעיית התכנון, ולאחר מכן לפתח משוואות לפתרון עבור אלה לא ידועים. כמו ברוב עיצוב האלקטרוניקה, מספר המשוואות יהיה קטן ממספר הלא ידועים. המגבלות הנוספות נקבעות כדי לעמוד ביעדים כלליים מסוימים (למשל, עלות מינימלית, פחות וריאציה בביצועים עקב שינויים בפרמטרים).
10.1 מגבר CS
בקטע זה מוצג נוהל העיצוב של מגבר CS. אנו נפחית את JFET ואת מגבר ה- MOSFET דלדול האספקה לנוהל מאורגן. אמנם זה עשוי להיראות
כדי להפחית את העיצוב לתהליך שגרתי מאוד, עליך לשכנע את עצמך שאתה מבין את מקורו של כל שלב, מאחר וייתכן כי יידרשו מספר וריאציות. אם כל מה שאתה עושה כדי לתכנן מגבר CS הוא "לחבר" ללא מחשבה לשלבים שאנחנו מציגים, אתה חסר את כל העניין של הדיון הזה. כמהנדס אתה מבקש לעשות דברים שכן לֹא שגרה. הפחתת התיאוריה לגישה מאורגנת היא מה שתעשו. אתה לא פשוט ליישם את הגישות שאחרים כבר עשו בשבילך.
מגברים מתוכננים לעמוד בדרישות רווח בהנחה שהמפרט הרצוי נמצא בטווח הטרנזיסטור. בדרך כלל מוגדרים מתח האספקה, התנגדות העומס, עליית המתח והתנגדות הקלט (או השגת הזרם). תפקידו של המעצב הוא לבחור את ערכי ההתנגדות R1, R2, RD, ו RS. עיין בתרשים 40 תוך כדי ביצוע השלבים בהליך. הליך זה מניח שמכשיר נבחר ומאפייניו ידועים.
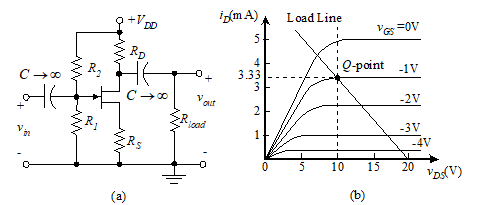
איור 40 JFET CS מגבר
ראשית, בחר נקודת Q באזור רוויה של עקומות FET אופייני. עיין בעקומות איור 40 (b) לדוגמה. זה מזהה VDSQ, VGSQ, ו IDQ.
אנחנו עכשיו לפתור עבור שני נגדים בלולאה פלט, RS ו RD. מאחר שישנם שני אלמונים, אנו דורשים שתי משוואות עצמאיות. אנחנו מתחילים בכתיבת dc משוואת KVL סביב לולאת מקור הניקוז,
![]() (58)
(58)
פתרון לסכום של שני נגדים התשואות
![]() (59)
(59)
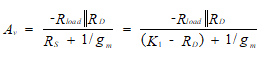 (60)
(60)
ההתנגדות, RD, הוא המוכר היחיד במשוואה זו. פתרון עבור RD תוצאות במשוואה ריבועית עם שני פתרונות, אחד שלילי ואחד חיובי. אם הפתרון החיובי גורם לכך RD > K1, ובכך מרמז שלילי RS, יש לבחור נקודת Q חדשה (כלומר, להפעיל מחדש את העיצוב). אם התשואה החיובית תשואות RD < K1, אנחנו יכולים להמשיך.
עכשיו RD ידוע, אנו פותר עבור RS באמצעות משוואה (59), משוואת לולאה לניקוז המקור.
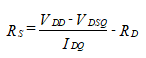 (61)
(61)
עם RD ו RS ידוע, אנחנו צריכים רק למצוא R1 ו R2.
אנו מתחילים על ידי כתיבה מחדש של משוואת KVL עבור לולאת מקור השער.
![]() (62)
(62)
המתח, VGS, הוא של קוטביות מנוגד מ VDD. לכן המונח IDQRS חייב להיות גדול מ VGSQ בסדר גודל. אחרת, VGG תהיה קוטביות הפוכה מ VDD, אשר אינו אפשרי על פי משוואה (62).
אנחנו עכשיו לפתור עבור R1 ו R2 בהנחה כי VGG מצא את אותה קוטביות as VDD. ערכי הנגד נבחרו על ידי מציאת הערך של RG מן המשוואה הנוכחית רווח או התנגדות הקלט. אנחנו פונים R1 ו R2.
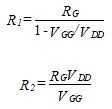 (63)
(63)
נניח עכשיו כי משוואה (62) תוצאות ב VGG כי יש קוטביות הפוכה of VDD. לא ניתן לפתור R1 ו R2. הדרך המעשית להמשיך היא לתת VGG = 0 V. לפיכך, ![]() . מאז VGG צוין על ידי משוואה (62), הערך המחושב בעבר של RS עכשיו צריך להיות שונה.
. מאז VGG צוין על ידי משוואה (62), הערך המחושב בעבר של RS עכשיו צריך להיות שונה.
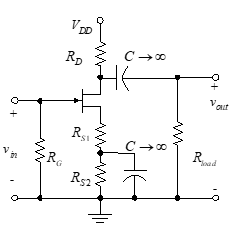
איור 41 - מגבר CS
באיור 41, שבו נעשה שימוש בקבל כדי לעקוף חלק RS, אנו מפתחים את הערך החדש של RS באופן הבא:
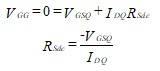 (64)
(64)
הערך של RNDC is RS1 + RS2 ואת הערך של Rשלפוחית is RS1.
עכשיו שיש לנו חדש RNDC, עלינו לחזור על כמה שלבים מוקדמים יותר בתכנון. אנחנו שוב קובעים RD באמצעות KVL עבור לולאה לניקוז המקור.
![]() (65)
(65)
בעיית התכנון הופכת כעת לחישוב של שניהם RS1 ו RS2 במקום למצוא רק מקור אחד.
עם ערך חדש עבור RD of K1 רNDC, אנחנו הולכים הביטוי מתח מתח של משוואה (60) עם Rשלפוחית משמש עבור זה ac משוואה במקום RS. יש להוסיף את השלבים הנוספים הבאים לנוהל התכנון:
אנחנו מוצאים Rשלפוחית (וזה פשוט RS1) ממשוואת רווח המתח
![]() (66)
(66)
Rשלפוחית הוא המוכר היחיד במשוואה זו. פתרון עבור זה, אנו מוצאים
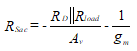 (67)
(67)
נניח עכשיו Rשלפוחית נמצא חיובי, אך פחות RNDC. זהו המצב הרצוי מאז
![]() (68)
(68)
אז העיצוב שלנו הוא שלם
![]() (69)
(69)
נניח ש Rשלפוחית נמצא חיובי אבל יותר מֵאֲשֶׁר RNDC. מגבר לא יכול להיות מתוכנן עם רווח מתח ו- Q נקודה כפי שנבחרה. יש לבחור נקודת Q חדשה. אם רווח המתח גבוה מדי, ייתכן שלא ניתן יהיה להשפיע על העיצוב עם נקודת Q כלשהי. טרנזיסטור אחר עשוי להיות נחוץ או להשתמש בשני שלבים נפרדים עשויים להיות נדרשים.
10.2 מגבר התקליטורים
כעת אנו מציגים את נוהל העיצוב של מגבר CD JFET. הכמויות הבאות מפורטות: רווח שוטף, התנגדות עומס ו VDD. ניתן לציין התנגדות קלט במקום רווח נוכחי. עיין במעגל באיור 39 בזמן שאתה לומד את ההליך הבא. שוב אנו מזכירים לך שתהליך צמצום התיאוריה למכלול שלבים הוא החלק החשוב בדיון זה - ולא הצעדים בפועל.
ראשית בחר נקודת Q במרכז עקומות המאפיין FET בעזרת איור 20 ("פרק 3: טרנזיסטור אפקט שדה צומת (JFET)"). שלב זה קובע VDSQ, VGSQ, IDQ ו gm.
אנחנו יכולים לפתור עבור הנגד מחובר למקור על ידי כתיבת dc משוואת KVL סביב לולאת הניקוז למקור.
![]() (70)
(70)
שממנו אנו מוצאים את dc ערך של RS,
![]() (71)
(71)
אנחנו מוצאים את ac ערך ההתנגדות, Rשלפוחית, מתוך משוואת הרווח הנוכחי reranged, משוואה (55).
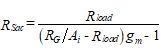 (72)
(72)
איפה RG = Rin. אם התנגדות הקלט אינה מצוינת, אפשר Rשלפוחית = RNDC ולחשב את ההתנגדות קלט משוואה (72). אם התנגדות הקלט אינה גבוהה מספיק, ייתכן שיהיה צורך לשנות את המיקום Q-point.
If Rin צוין, יש צורך לחשב Rשלפוחית משוואה (72). במקרים כאלו, Rשלפוחית שונה מ RNDC, אז אנחנו עוברים חלק RS עם קבלים.
כעת אנו מפנים את תשומת לבנו למעגל ההטיה של הקלט. אנחנו קובעים VGG באמצעות המשוואה,
![]() (73)
(73)
אין היפוך פאזה מיוצר מגבר מקור FET מגבר ו VGG הוא בדרך כלל של אותה קוטביות כמו מתח האספקה.
עכשיו VGG ידוע, אנו קובעים את הערכים של R1 ו R2 מן המקבילה המקבילה של Thevenin של מעגל הטיה
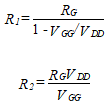 (74)
(74)
בדרך כלל קיים זרם ניקוז מספיק במדד SF כדי לפתח את מתח הקוטביות המנוגד הנדרש כדי לקזז את המתח השלילי הנדרש על ידי שער JFET. לפיכך, ניתן להשתמש בהתעמלות חלוקת מתח נורמלית.
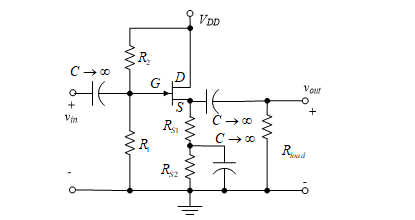
איור 44 - מגבר תקליטורים עם חלק של RS עקף
כעת אנו חוזרים לבעיה של ציון ההתנגדות קלט. אנחנו יכולים להניח כי חלק RS הוא עקף, כמו באיור 44, אשר מוביל ערכים שונים של Rשלפוחית ו RNDC. אנו משתמשים משוואה (71) כדי לפתור עבור RNDC. לאחר מכן, אנו נותנים RG שווה את הערך שצוין Rin, ולהשתמש משוואה (72) כדי לפתור עבור Rשלפוחית.
אם Rשלפוחית מחושב מעל קטן מ RNDC, העיצוב נעשה על ידי עקיפת RS2 עם קבלים. תזכור את זה Rשלפוחית = RS1 ו RNDC = RS1 + RS2. אם מאידך גיסא, Rשלפוחית גדול מ RNDC, יש להעביר את נקודת ה- Q למיקום אחר. אנו בוחרים קטן יותר VDS ובכך גורם מתח מוגבר להישמט על פני RS1 + RS2, מה שהופך RNDC יותר גדול. אם VDS לא ניתן לצמצם מספיק כדי להפוך RNDC גדול מ Rשלפוחית, אז המגבר לא יכול להיות מתוכנן עם הרווח הנוכחי הנתון, Rin, וסוג FET. אחד משלושת המפרטים האלה חייב להשתנות, או שלב הבמה השני צריך לשמש כדי לספק את הרווח הנדרש.
10.3 מגבר Bootstrap SF
כעת אנו בודקים וריאציה של מגבר התקליטורים הידועה בשם SF (או תקליטור) bootstrap מגבר FET. מעגל זה הוא מקרה מיוחד של SF קרא מעגל והוא מאויר באיור 45.
כאן הטיה מפותחת על פני רק חלק של הנגד המקור. זה מפחית את הצורך במעקף קבלים על פני חלק של הנגד המקור ובכך משיגה התנגדות קלט הרבה יותר גדול מאשר בדרך כלל ניתן להשיג. עיצוב זה מאפשר לנו לנצל את המאפיינים של עכבה גבוהה של FET ללא שימוש ערך גבוה של נגד השער, RG.
המעגל המקביל של איור 46 משמש להערכת פעולת המעגל
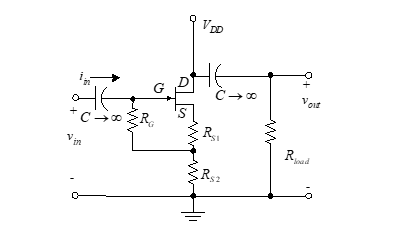
איור 45 - עוקב המקור Bootstrap
אנו מניחים זאת iin הוא קטן מספיק כדי משוער הנוכחי ב RS2 as i1. מתח המוצא נמצא לאחר מכן
![]() (75)
(75)
איפה
![]() (76)
(76)
אם ההנחה לגבי iin אינו תקף, מוחלף בביטוי
![]() (77)
(77)
משוואת KVL בתשומות התשומות vin באופן הבא:
![]() (78)
(78)
הנוכחי, i1, נמצא ממערכת יחסים עכשווית,
![]() (79)
(79)
שילוב משוואות (79) ו (78) התשואות,
![]() (80)
(80)
משוואה שנייה עבור vin הוא פיתח סביב לולאה דרך RG ו RS2 כדלהלן.
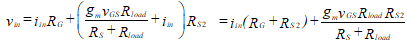 (81)
(81)
אנחנו מסלקים vin על ידי הגדרת משוואה (80) שווה למשוואה (81) ולפתור עבור iin כדי להשיג
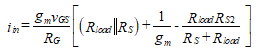 (82)
(82)
התנגדות הקלט, Rin = vin/iin, נמצא על ידי חלוקת המשוואה (81) על ידי משוואה (82) עם התוצאה,
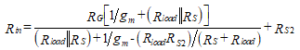 (83)
(83)
RG הוא היחיד לא ידוע במשוואה זו, כך שנוכל לפתור כדי להשיג,
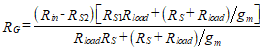 (84)
(84)
הרווח הנוכחי הוא
![]() (85)
(85)
כעת אנו יכולים להשתמש במשוואות הנגזרות מוקדם יותר עם התצפית כי RS - RS2 = RS1 כדי לפתור את הרווח הנוכחי.
![]() (86)
(86)
רווח המתח הוא
![]() (87)
(87)
שים לב שהמכנה במשוואה (84) גדול מהמספר, ובכך מראה זאת RG <(Rin-RS2). זה מוכיח כי התנגדות קלט גדול ניתן להשיג ללא צורך באותו סדר גודל RG.

 זרם - 10. תכנון מגבר FET
זרם - 10. תכנון מגבר FET קודם - 9. ניתוח מגבר FET
קודם - 9. ניתוח מגבר FET
