1. אידיאלי op-amps
אידיאלי op-amps
סעיף זה משתמש ב- מערכות הגישה להציג את היסודות של מגברים תפעוליים אידיאליים. לפיכך, אנו רואים את המגבר אופ כמו בלוק עם מסופי קלט ו פלט. אנחנו לא עוסקים כרגע בהתקנים האלקטרוניים האישיים בתוך המגבר.
מגבר אופ הוא מגבר כי הוא מופעל לעתים קרובות על ידי שני מתח חיובי ואספקה שלילית. זה מאפשר את מתח המוצא כדי הנדנדה הן מעל ומתחת פוטנציאל הקרקע. המגבר אופ מוצא יישום רחב במערכות אלקטרוניות לינאריות רבות.
שם מגבר מבצעי נגזר מאחד השימושים המקוריים של מעגלי אופ-אמפר; לבצע מתמטית פעולות במחשבים אנלוגיים. יישום מסורתי זה נדון בהמשך פרק זה. מגבירי אופציה מוקדמים השתמשו בקלט הפוך יחיד. שינוי מתח חיובי בקלט גרם לשינוי שלילי בפלט.
לפיכך, כדי להבין את הפעולה של op-amp, יש צורך להכיר תחילה את הרעיון של מקורות מבוקרים (תלוי) שכן הם מהווים את הבסיס של מודל op-amp.
1.1 מקורות תלויים
מקורות תלויים (או מבוקרים) מייצרים מתח או זרם שערכם נקבע על ידי מתח או זרם הקיים במיקום אחר במעגל. לעומת זאת, מכשירים פסיביים מייצרים מתח או זרם שערכם נקבע על ידי מתח או זרם קיים באותו מקום במעגל. הן המתח העצמאי והן התלות והמקורות הנוכחיים הם גורמים פעילים. כלומר, הם מסוגלים לספק כוח למכשיר חיצוני כלשהו. אלמנטים פסיביים אינם מסוגלים לייצר חשמל, למרות שהם יכולים לאחסן אנרגיה למשלוח במועד מאוחר יותר, כמו במקרה של קבלים ומשרנים.
האיור שלהלן ממחיש תצורה מעגל שווה של מכשיר הגברה המשמש לעתים קרובות ניתוח מעגלים. הימנית![]() הנגד הוא העומס. אנו מוצאים את המתח ואת הרווח הנוכחי של מערכת זו. מתח מתח, Av מוגדר כיחס בין מתח המוצא למתח הכניסה. באופן דומה, הרווח הנוכחי, Ai הוא היחס בין זרם הזרם לקלט הנוכחי.
הנגד הוא העומס. אנו מוצאים את המתח ואת הרווח הנוכחי של מערכת זו. מתח מתח, Av מוגדר כיחס בין מתח המוצא למתח הכניסה. באופן דומה, הרווח הנוכחי, Ai הוא היחס בין זרם הזרם לקלט הנוכחי.
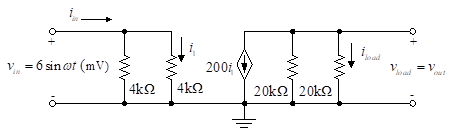
איור 1 - מעגל שווה של מצב מוצק מכשיר הגברה
זרם הקלט הוא:
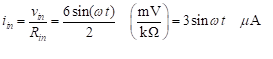
הזרם בנגד השני, i1, נמצא ישירות מחוק אוהם:
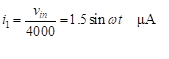
(2)
מתח המוצא ניתן על ידי:
(3)
במשוואה (3) 12 מציין שילוב מקביל של נגדים. זרם המוצא נמצא ישירות מחוק אוהם.
(4)
המתח והרווחים הנוכחיים נמצאים אז על ידי יצירת היחס:
(5)
(6)
1.2 מגבר תפעולי
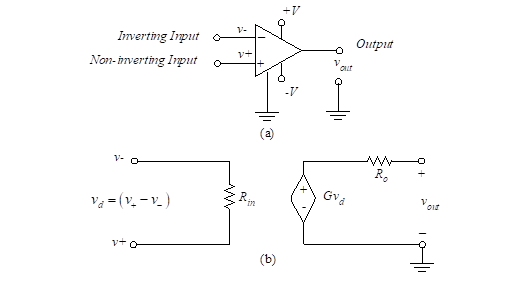
איור 2 - מגבר תפעולי ומעגל שווה ערך
Figure תצורה 2 () מציג את הסמל עבור המגבר התפעולי, ואת איור 2 (ב) מציג מעגל שווה שלה. מסופי הקלט הם v+ ו v-. מסוף היציאה הוא vהַחוּצָה. חיבורי אספקת החשמל נמצאים ב +V, -V מסופי קרקע. חיבורי החשמל הם לעתים קרובות מושמט מרישומים סכמטיים. הערך של מתח המוצא מוגבל +V ו -V שכן אלה הם המתחים החיוביים והשליליים ביותר במעגל.
המודל מכיל מקור מתח תלוי המתח שלו תלוי בהפרש מתח הכניסה בין v+ ו v-. שני מסופי קלט ידועים בשם לא היפוך ו היפוך תשומות בהתאמה. באופן אידיאלי, התפוקה של המגבר אינה תלויה בגודלם של שני מתח הקלט, אלא רק בהבדל ביניהם. אנו מגדירים את מתח כניסה דיפרנציאלי, vd, כהבדל,
(7)
מתח המוצא הוא פרופורציונלי למתח הקלט הדיפרנציאלי, ואנו מייחסים את היחס כרווח לולאה פתוחה, G. לפיכך, מתח המוצא הוא
(8)
כדוגמה, קלט של ![]() (E הוא בדרך כלל משרעת קטנה) מוחל על קלט שאינו ממיר עם מסוף הפוכה מקורקע, מייצרת
(E הוא בדרך כלל משרעת קטנה) מוחל על קלט שאינו ממיר עם מסוף הפוכה מקורקע, מייצרת ![]() על הפלט. כאשר אות המקור זהה מוחל על קלט הפוך עם מסוף שאינו הופך מקורקע, הפלט הוא
על הפלט. כאשר אות המקור זהה מוחל על קלט הפוך עם מסוף שאינו הופך מקורקע, הפלט הוא ![]() .
.
עכבת הקלט של המגבר אופ מוצג כהתנגדות באיור 2 (b).
עכבת המוצא מיוצגת בדמות כהתנגדות, Ro.
מגבר תפעולי אידיאלי מאופיין כדלקמן:
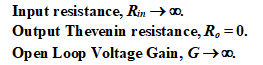
אלה הם בדרך כלל קירוב טוב הפרמטרים של אמיתי מגברים. פרמטרים אופייניים של מגברי אופטיים אמיתיים הם:
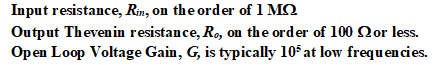
השימוש במגבי אופ אידיאלי כדי משוער אמיתי מגברי אופ הוא אפוא פישוט יקר עבור ניתוח מעגל.
תן לנו לחקור את המשמעות של רווח לולאה פתוחה להיות אינסופי. אם אנחנו לשכתב משוואה (8) ![]() באופן הבא:
באופן הבא:
(9)
ולתת G גישה אינסופית, אנחנו רואים את זה
(10)
משוואה (10) התוצאות על ידי התבוננות כי מתח המוצא אינו יכול להיות אינסופי. הערך של מתח המוצא מוגבל על ידי ערכי אספקת החשמל החיוביים ושליליים. משוואה (10) עולה כי המתח בשני המסופים זהים:
(11)
לכן, השוויון של משוואה (11) מוביל אותנו לומר יש קצר קצר בין מסופים קלט.
מאז התנגדות הקלט של המגבר אופ אידיאלי הוא אינסופי, הנוכחי לתוך כל קלט, מסוף היפוך מסוף שאינו הפוך, הוא אפס.
כאשר אמיתי am-amps משמשים במצב הגברה ליניארית, רווח גדול מאוד, משוואה (11) הוא קירוב טוב. עם זאת, מספר יישומים עבור אמיתי am-amps להשתמש במכשיר במצב לא לינארית. הקירוב של משוואה (11) אינו תקף עבור מעגלים אלה.
אף על פי שלמגנטים אופטיים אופייניים יש מתח גבוה, רווח זה משתנה בתדירות. מסיבה זו, מגבר אופ אינו משמש בדרך כלל בצורה שמוצג באיור 2 (א). תצורה זו נקראת לולאה פתוחה כי אין משוב מפלט קלט. אנו רואים מאוחר יותר, בעוד תצורת לולאה פתוחה שימושי עבור יישומים המשווה, תצורה נפוצה יותר עבור יישומים לינאריים הוא מעגל סגור לולאה עם משוב.
אלמנטים חיצוניים משמשים ל"משוב "חלק מאות הפלט לכניסה. אם אלמנטים המשוב ממוקמים בין הפלט לקלט ההפוך, הרווח של הלולאה הסגורה פוחת מכיוון שחלק מהפלט גורע מהקלט. נראה בהמשך כי משוב לא רק מקטין את הרווח הכללי, אלא הוא גם גורם לכך שהרווח פחות רגיש לערך G. עם משוב, הרווח במעגל הסגור תלוי יותר באלמנטים במעגל המשוב, ופחות באופציה הבסיסית. רווח מתח אמפר, G. למעשה, רווח הלולאה הסגורה אינו תלוי בערך של G- זה תלוי רק בערכי אלמנטים המעגל החיצוני.
איור (3) מדגים שלב משוב שלילי אחד במעגל אופ-אמפר.
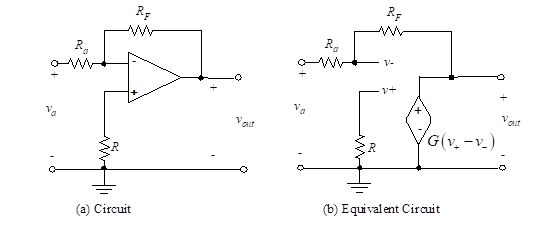
איור 3 - ההופך מגבר אופ
לכן, ננתח את המעגל בחלק הבא. לעת עתה, שים לב כי נגד יחיד, RF, משמש לחיבור מתח המוצא, vהַחוּצָה אל הקלט ההפוכה, v-.
עוד נגד, Ra מחובר מקלט הפוך, v-, למתח הקלט, va. נגד שלישי, R ממוקם בין הקלט שאינו מקרקע לקרקע.
מעגלים באמצעות op-amps, נגדים וקבלים ניתן להגדיר לבצע פעולות שימושיות רבות כגון סיכום, חיסור, שילוב, הבחנה, סינון, השוואה, והגברה.
1.3 שיטת הניתוח
אנו מנתחים מעגלים תוך שימוש בשני המאפיינים החשובים של אופ-אמפר:
- המתח בין v+ ו v- הוא אפס, או v+ v v-.
- הנוכחי לתוך שניהם v+ ו v- הטרמינל הוא אפס.
תצפיות פשוטות אלה מובילות לפרוצדורה לניתוח כל מעגל אופ-אמפר אידיאלי כדלקמן:
- כתוב את משוואת הצומת המשפטית Kirchhoff הנוכחית על מסוף שאינו הפוכה, v+.
- כתוב את משוואת הצומת החוקית של Kirchhoff הנוכחית במסוף היפוך, v-.
- לקבוע v+ v v- ולפתור עבור הרצוי לולאה סגורה הרווחים.
כשאתה מיישם את חוקי קירכהוף, זכור שהזרם לשני v+ ו v- הטרמינל הוא אפס.

 זרם - 1. מגברים אופטימליים
זרם - 1. מגברים אופטימליים מגברים תפעוליים אידאליים הקדמה
מגברים תפעוליים אידאליים הקדמה