 TINACloud को आमंत्रित करने के लिए नीचे दिए गए उदाहरण सर्किट पर क्लिक करें या टैप करें और उन्हें ऑनलाइन विश्लेषण करने के लिए इंटरएक्टिव डीसी मोड का चयन करें।
TINACloud को आमंत्रित करने के लिए नीचे दिए गए उदाहरण सर्किट पर क्लिक करें या टैप करें और उन्हें ऑनलाइन विश्लेषण करने के लिए इंटरएक्टिव डीसी मोड का चयन करें। उदाहरणों को संपादित करने या अपने स्वयं के सर्किट बनाने के लिए टिनक्लाउड तक कम लागत पहुंचें
इसमें और निम्नलिखित अध्यायों में, हम एक बहुत ही महत्वपूर्ण विषय प्रस्तुत करेंगे: एसी, या अल्टरनेटिंग करंट। प्रत्यावर्ती धारा नाम बहुत सटीक नहीं है और सामान्य रूप से साइनसोइडल वोल्टेज और धाराओं के साथ सर्किट को कवर करता है; हालाँकि, प्रत्यावर्ती धारा का अर्थ किसी भी मनमाने वर्तमान तरंग से भी हो सकता है। एसी वोल्टेज का महत्व यह है कि इस तरह के वोल्टेज का उपयोग दुनिया भर में घरों और उद्योग में मुख्य विद्युत ऊर्जा स्रोत के लिए किया जाता है। यह कई इलेक्ट्रॉनिक्स, दूरसंचार और औद्योगिक अनुप्रयोगों के लिए भी आधार है।
साइनसोइडल वेवफॉर्म और उनसे जुड़े सर्किट को संभालने के लिए, हम एक सरल और सुरुचिपूर्ण विधि का उपयोग करेंगे, जिसे चरण की विधि कहा जाता है। चरण जटिल संख्याओं के गुणों पर आधारित होते हैं, जो साइनसोइडल मात्रा का प्रतिनिधित्व करने के लिए आदर्श होते हैं। इस अध्याय में, हम जटिल संख्या और उनके संचालन के बारे में मुख्य तथ्यों का सारांश देंगे। हम यह भी दिखाएंगे कि टीना के दुभाषिए ने जटिल संख्याओं के साथ गणना करना आसान कैसे बनाया।
जटिल संख्या में दो भाग होते हैं, a असली हिस्सा (x), जो एक वास्तविक संख्या है, और एक तथाकथित है काल्पनिक हिस्सा (y), जो एक वास्तविक संख्या से गुणा है 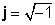
z = x + jy
जहां 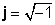
जटिल संख्या के उदाहरण:
z 1 = 1 + j
z 2 = 4-2 j
z 3 = 3- 5j
मूल संख्याओं को मूल रूप से सत्रहवीं शताब्दी में बहुपद की जड़ों का प्रतिनिधित्व करने के लिए पेश किया गया था जो कि वास्तविक संख्याओं के साथ अकेले प्रतिनिधित्व नहीं कर सकते थे। उदाहरण के लिए, समीकरण x की जड़ें2 + 2x + 2 = 0 के रूप में वर्णित किया जा सकता है 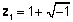
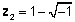
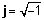
जटिल संख्याओं का ज्यामितीय प्रतिनिधित्व
आयताकार रूप
क्योंकि एक जटिल संख्या को हमेशा उसके वास्तविक और जटिल भागों में अलग किया जा सकता है, हम एक जटिल संख्या को दो-आयामी विमान पर एक बिंदु के रूप में दर्शा सकते हैं। एक जटिल संख्या का वास्तविक हिस्सा वास्तविक अक्ष पर बिंदु का प्रक्षेपण है, और संख्या का काल्पनिक हिस्सा काल्पनिक अक्ष पर प्रक्षेपण है। जब एक जटिल संख्या को वास्तविक और काल्पनिक भागों के योग के रूप में दर्शाया जाता है, तो हम कहते हैं कि यह अंदर है आयताकार or बीजगणितीय रूप.
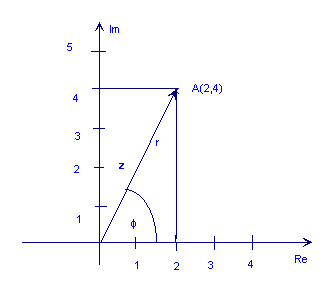
निम्नलिखित आंकड़ा जटिल संख्या दिखाता है z = 2 + 4j
ध्रुवीय और घातीय रूप
जैसा कि आप ऊपर की आकृति से देख सकते हैं, बिंदु A को तीर की लंबाई से भी दर्शाया जा सकता है, r (इसे पूर्ण मान, परिमाण या आयाम भी कहा जाता है), और इसका कोण (या चरण), φ सकारात्मक क्षैतिज अक्ष के लिए एक वामावर्त दिशा में सापेक्ष। यह है ध्रुवीय एक जटिल संख्या का रूप। इसे r ∠ के रूप में दर्शाया गया है φ.
अगला कदम बहुत महत्वपूर्ण है। ध्रुवीय रूप में एक जटिल संख्या भी लिखी जा सकती है घातीय प्रपत्र:
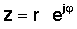
यह सरल अभिव्यक्ति इस मायने में विशिष्ट है कि इसकी सामान्य संख्या के बजाय घातांक में एक काल्पनिक संख्या है। यह जटिल घातांक एक वास्तविक तर्क के साथ घातीय फ़ंक्शन से बहुत अलग व्यवहार करता है। जबकि ईx x> 0 को बढ़ाने के लिए परिमाण में तेजी से बढ़ता है और x <0, फ़ंक्शन के लिए घट जाता है 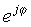
आयलर का सूत्र आयताकार, ध्रुवीय और जटिल संख्याओं के घातीय रूपों के बीच एक एकीकृत लिंक प्रदान करता है:
z = x + jय = पुनः jφ = आर (कॉस φ + j पाप φ )
जहां 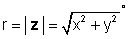
और φ = तन-1 (Y / एक्स)।
ऊपर हमारे उदाहरण के लिए, z = 2 + 4j:
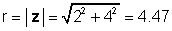
φ = तन-1 (4 / 2) = 63.4 °
इसलिये 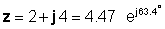
या ठीक इसके विपरीत:
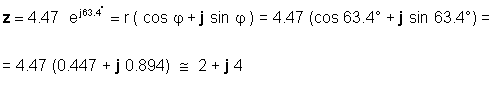
आपको आवेदन के आधार पर दोनों रूपों का उपयोग करने की आवश्यकता होगी। उदाहरण के लिए, जोड़ या घटाव स्पष्ट रूप से करना आसान होता है जब संख्याएं आयताकार रूप में होती हैं, जबकि गुणा और भाग करना आसान होता है जब संख्याएं घातीय रूप में होती हैं।
जटिल संख्या के साथ संचालन
जटिल संख्याओं के साथ किए जाने वाले ऑपरेशन वास्तविक संख्याओं के समान हैं। नियम और कुछ नई परिभाषाएँ नीचे संक्षेप में दी गई हैं।
संचालन जे
के साथ संचालन j बस काल्पनिक इकाई की परिभाषा का पालन करें,


तेजी से और सही तरीके से काम करने में सक्षम होने के लिए, आपको इन नियमों को याद रखना चाहिए:
j 2 = -1
j 3 =-j
j 4 =1
1/j = -j
j2 = -1 बस की परिभाषा से इस प्रकार है 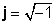
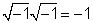
1 के लिए /j, हम 1 / गुणा करते हैंjby j / j = 1 और प्राप्त करें j/ (dd) = j / (- 1) = -j.
जटिल सन्युग्म
एक जटिल संख्या का जटिल संयुग्मन आसानी से प्राप्त होता है और काफी महत्वपूर्ण होता है। आयताकार रूप में एक जटिल संख्या के जटिल संयुग्म को प्राप्त करने के लिए, बस काल्पनिक भाग के संकेत को बदलें। घातीय रूप में एक संख्या के लिए ऐसा करने के लिए, अपने पूर्ण मूल्य को समान रखते हुए जटिल संख्या के कोण के संकेत को बदलें।
एक जटिल संख्या के जटिल संयुग्म z द्वारा अक्सर निरूपित किया जाता है z*.
जटिल संख्या को देखते हुए z= एक + jबी, इसका जटिल संयुग्म है z*= एक करने के लिए jb.
If z घातीय रूप में दिया गया है, 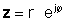
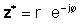
उपरोक्त परिभाषाओं का उपयोग करते हुए, यह देखना आसान है कि एक जटिल संख्या को इसके जटिल संयुग्म से गुणा किया जाता है जो जटिल संख्या के निरपेक्ष मान का वर्ग देता है:
ZZ* = आर2 = एक2 + b2
इसके अलावा, किसी भी जटिल संख्या और इसके संयुग्म को जोड़कर या घटाकर, हमें निम्नलिखित संबंध मिलते हैं:
z + z * = 2a
इसलिये
Re (z) = a = ( z + z * ) / एक्सएनयूएमएक्स
इसी तरह:
z - z * =j2b
इसलिये
मैं हूँ(z) = बी = ( z -z * ) / एक्सएनयूएमएक्सj
सबूत:
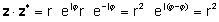
या वास्तविक और काल्पनिक भागों को गुणा करना और उपयोग करना j2= -1
ZZ* = (अ + jबी 0 ए - jख) = एक2+a jबी XNUMX ए jबी - jbjबी = ए2j2 = ए2 + b2
z + z* = एक + jb + a - jबी = 2a
z - z*= एक + jबी - ए + jबी =j2b
संख्यात्मक उदाहरण:
आयताकार रूप में:
z = 3 + j4
z* = 3- j4
ZZ * = 9 + 16 = 25
ध्रुवीय रूप में
z = 5 .53.13 XNUMX °
z * = 5 ∠- 53.13 °
घातांक रूप में:
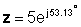
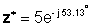
जोड़ और घटाव
जटिल संख्याओं का जोड़ और घटाव सीधा है-हमें केवल वास्तविक और काल्पनिक भागों को अलग-अलग जोड़ना होगा। उदाहरण के लिए, यदि
z1 = 3 - 4j और z2 = 2 + 3j
फिर
z1 + z2 = 3 - 4j + एक्सएनएनएक्स + एक्सएनएनएक्सj = 3 + एक्सएनएनएक्स - एक्सएनएनएक्सj + 3j = 5 - j
z1 - z2 = 3 - 4j - 2 - 3j = 3 - 2 - 4j - 3j = 1 - j7
जाहिर है, हमें इन कार्यों के लिए आयताकार रूप का उपयोग करना चाहिए। यदि संख्या घातीय या ध्रुवीय रूप में दी गई है, तो हमें उन्हें यूलर के सूत्र का उपयोग करके पहले आयताकार रूप में बदलना चाहिए, जैसा कि पहले दिया गया था।
गुणन
जटिल संख्याओं के गुणन के लिए दो विधियाँ हैं-
आयताकार रूप में दी गई जटिल संख्याओं का गुणन
ऑपरेशन को अंजाम देने के लिए, बस एक संख्या के वास्तविक और काल्पनिक भागों को दूसरे नंबर के वास्तविक और काल्पनिक भागों से मोड़ें और पहचान का उपयोग करें j2 = -1।
z1z2 = (ए1 + jb1) (ए2 + jb2) = ए1 a2 + jb1a2+ jb2a1 - बी1b2 = एक1 a2- बी1b2 + j(b1a2+ jb2a1)
जब जटिल संख्याओं को संख्यात्मक रूप से दिया जाता है, तो उपरोक्त सूत्र का उपयोग करना आवश्यक नहीं है। उदाहरण के लिए, चलो
z1 = 3 - 4j और z2 = 2 + 3j
घटकों के प्रत्यक्ष गुणन के साथ:
z1z2 = (3 - 4j) (2 + 3j) = एक्सएनयूएमएक्स- एक्सएनयूएमएक्सj +9j + 12 = 18 + j
या सूत्र का उपयोग कर: z1z2 = एक1 a2- बी1b2 + j(b1a2B +2a1)
z1z2 = 6 + 12 + j (-8 + 9) = 18 + j
हमें लगता है कि यदि आप सीधे घटकों को गुणा करते हैं तो आप सूत्र का उपयोग करने में त्रुटि की संभावना रखते हैं।
z1: = 3-4 * j
z2: = 2 + 3 * j
z1 * z2 = [18 + 1 * j]
गणित को एम के रूप में आयात करें
सीमैथ को सी के रूप में आयात करें
z1=जटिल('3-4j')
z2=जटिल('2+3j')
प्रिंट(“z1*z2=”,z1*z2)
ध्रुवीय या घातीय रूप में दी गई जटिल संख्याओं का गुणन
इस ऑपरेशन को करने के लिए, निरपेक्ष मूल्यों को गुणा करें और दो जटिल संख्याओं के कोणों को जोड़ें। करते हैं:
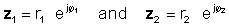
फिर घातीय कार्यों के गुणन के नियम का उपयोग करना:
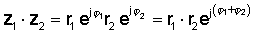
या ध्रुवीय रूप में
z1 z2 = आर1 r2 ∠ ∠1 + φ2
नोट: हमने गणना करते समय इस नियम का उपयोग किया है ZZ *ऊपर। चूंकि संयुग्म के कोण में मूल कोण का विपरीत चिन्ह होता है, एक जटिल संख्या जो अपने स्वयं के संयुग्म से गुणा होती है वह हमेशा एक वास्तविक संख्या होती है; अर्थात्, इसके पूर्ण मूल्य का वर्ग: ZZ * = आर2
उदाहरण के लिए, आइए:
z1 = 5 ° 30 ° और z2 = 4 60 -XNUMX °
फिर
z1z2 = 20 30 -XNUMX °
या घातीय रूप में
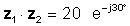
गुणा स्पष्ट रूप से सरल है जब संख्याएं ध्रुवीय या घातीय रूप में होती हैं।
हालाँकि, यदि आयताकार रूप में जटिल संख्याएँ दी गई हैं, तो आपको ऊपर दिखाए गए अनुसार गुणन को सीधे करने पर विचार करना चाहिए, क्योंकि अतिरिक्त संख्याएँ हैं यदि आप संख्याओं को गुणा करने से पहले ध्रुवीय रूप में बदलते हैं। विचार करने के लिए एक अन्य कारक यह है कि क्या आप चाहते हैं कि उत्तर आयताकार रूप में या ध्रुवीय / घातीय रूप में हों। उदाहरण के लिए, यदि दो संख्याएँ आयताकार रूप में हैं, लेकिन आप उनके उत्पाद को ध्रुवीय रूप में पसंद करेंगे, तो उन्हें तुरंत रूपांतरित करना और फिर उन्हें गुणा करना समझ में आता है।
विभाजन
जटिल संख्याओं के विभाजन की दो विधियाँ हैं-
आयताकार रूप में दिए गए जटिल संख्याओं का विभाजन
ऑपरेशन को अंजाम देने के लिए हर के गुणक द्वारा हर अंश और हर को गुणा करें। भाजक एक वास्तविक संख्या बन जाता है और विभाजन दो जटिल संख्याओं के गुणन में घट जाता है और एक वास्तविक संख्या से एक विभाजन, भाजक के निरपेक्ष मान का वर्ग हो जाता है।
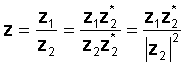
उदाहरण के लिए आइए:
z1 = 3 - 4j और z2 = 2 + 3j
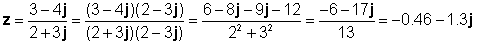
आइए टीना के दुभाषिया के साथ इस परिणाम की जाँच करें:
z1: = 3-4 * j
z2: = 2 + 3 * j
z1 / z2 = [- 461.5385m-1.3077 * j]
गणित को एम के रूप में आयात करें
सीमैथ को सी के रूप में आयात करें
z1=जटिल('3-4j')
z2=जटिल('2+3j')
प्रिंट(“z1/z2=”,z1/z2)
ध्रुवीय या घातीय रूप में दिए गए जटिल संख्याओं का विभाजन
ऑपरेशन करने के लिए, निरपेक्ष मान (परिमाण) को विभाजित करें और अंश के कोण से हर के कोण को घटाएं। करते हैं:
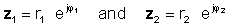
फिर घातीय कार्यों के विभाजन के नियम का उपयोग करना
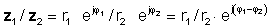
या ध्रुवीय रूप में
z 1 / z2 = आर1 / आर2 ∠ φ 1- φ 2
उदाहरण के लिए, आइए:
z 1 = 5 And 30 ° और z 2 = 2 ° -60 °
फिर
z 1 / z2 = 2.5 .90 XNUMX °
या घातीय और आयताकार रूपों में
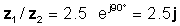
आइए टीना के दुभाषिया के साथ इस परिणाम की जाँच करें:
z1: = 5 * exp (जे * degtorad (30))
z2: = 2 * exp (जे * degtorad (-60))
z1 / z2 = [0 + 2.5 * j]
गणित को एम के रूप में आयात करें
सीमैथ को सी के रूप में आयात करें
z1=5*(c.exp(complex(0,m.radians(30))))
z2=2*(c.exp(complex(0,m.radians(-60))))
प्रिंट(“z1/z2=”,z1/z2)
विभाजन स्पष्ट रूप से सरल है जब संख्याएं ध्रुवीय या घातीय रूप में होती हैं।
हालाँकि, यदि आयताकार रूप में जटिल संख्याएँ दी गई हैं, तो आपको ऊपर दिखाए गए अनुसार जटिल संयुग्म विधि का उपयोग करके सीधे विभाजन करने पर विचार करना चाहिए, क्योंकि अतिरिक्त चरण हैं यदि आप संख्याओं को विभाजित करने से पहले ध्रुवीय रूप में बदलते हैं। विचार करने के लिए एक अन्य कारक यह है कि क्या आप चाहते हैं कि उत्तर आयताकार रूप में या ध्रुवीय / घातीय रूप में हों। उदाहरण के लिए, यदि दो संख्याएँ आयताकार रूप में हैं, लेकिन आप ध्रुवीय रूप में उनके भागफल को पसंद करेंगे, तो उन्हें तुरंत रूपांतरित करना और फिर उन्हें विभाजित करना समझ में आता है।
अब हम अधिक संख्यात्मक समस्याओं द्वारा जटिल संख्याओं के उपयोग को स्पष्ट करते हैं। हमेशा की तरह, हम टीना के इंटरप्रेटर का उपयोग करके अपने समाधानों की जांच करेंगे। इंटरप्रिटर रेडियन के साथ काम करता है, लेकिन इसमें रेडियन के डिग्री या इसके विपरीत रूपांतरण के मानक मानक हैं।
उदाहरण 1 ध्रुवीय प्रतिनिधित्व प्राप्त करें:
z = 12 - j 48
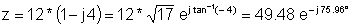
z: = 12-j * 48;
पेट (z) = [49.4773]
चाप (z) = [- 1.3258]
radtodeg (चाप (z)) = [- 75.9638]
गणित को एम के रूप में आयात करें
सीमैथ को सी के रूप में आयात करें
z=12-कॉम्प्लेक्स(48j)
प्रिंट(“abs(z)=”,abs(z))
प्रिंट(“arc(z)=”,c.phase(z))
प्रिंट करें ("डिग्री(चाप(z))=",m.डिग्री(c.phase(z)))
उदाहरण 2 आयताकार प्रतिनिधित्व प्राप्त करें:
z = एक्सएनयूएमएक्स ई j 125 °
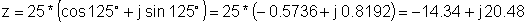
z: = 25 * exp (जे * (degtorad (125)));
z = [- 14.3394 + 20.4788 * j]
पुन (z) = [- 14.3394]
इम (z) = [20.4788]
गणित को एम के रूप में आयात करें
सीमैथ को सी के रूप में आयात करें
z=25*c.exp(complex(0,m.radians(125)))
प्रिंट(“z=”,z)
प्रिंट करें ("वास्तविक (z) =", z.real)
प्रिंट(“imag(z)=”,z.imag)
उदाहरण 3 निम्नलिखित जटिल संख्याओं के ध्रुवीय निरूपण का पता लगाएं:
z 1 = 12 + j 48 z2 = 12 - j48 z3= -12 + j 48 z4= -12 - j 48
सभी चार संख्याओं का पूर्ण मान समान है क्योंकि निरपेक्ष मान संकेतों से स्वतंत्र है। केवल कोण अलग हैं।
z1: = 12 + j * 48;
पेट (z1) = [49.4773]
चाप (z1) = [1.3258]
radtodeg (चाप (z1)) = [75.9638]
z2: = 12-j * 48;
पेट (z2) = [49.4773]
चाप (z2) = [- 1.3258]
radtodeg (चाप (z2)) = [- 75.9638]
z3: = - 12 + j * 48;
पेट (z3) = [49.4773]
चाप (z3) = [1.8158]
radtodeg (चाप (z3)) = [104.0362]
z4: = - 12-j * 48:
पेट (z4) = [49.4773]
चाप (z4) = [- 1.8158]
radtodeg (चाप (z4)) = [- 104.0362]
गणित को एम के रूप में आयात करें
सीमैथ को सी के रूप में आयात करें
z1=जटिल('12+48j')
प्रिंट(“abs(z1)=”,abs(z1))
प्रिंट(“arc(z1)=”,c.phase(z1))
प्रिंट करें ("डिग्री(चाप(z1))=",m.डिग्री(c.phase(z1)))
z2=जटिल('12-48j')
प्रिंट(“abs(z2)=”,abs(z2))
प्रिंट(“arc(z2)=”,c.phase(z2))
प्रिंट करें ("डिग्री(चाप(z2))=",m.डिग्री(c.phase(z2)))
z3=जटिल('-12+48j')
प्रिंट(“abs(z3)=”,abs(z3))
प्रिंट(“arc(z3)=”,c.phase(z3))
प्रिंट करें ("डिग्री(चाप(z3))=",m.डिग्री(c.phase(z3)))
z4=जटिल('-12-48j')
प्रिंट(“abs(z4)=”,abs(z4))
प्रिंट(“arc(z4)=”,c.phase(z4))
प्रिंट करें ("डिग्री(चाप(z4))=",m.डिग्री(c.phase(z4)))
टीना का चाप () फ़ंक्शन किसी भी जटिल संख्या के कोण को निर्धारित करता है, स्वचालित रूप से इसे चार में से एक में सही ढंग से रखता है।
हालांकि, तन का उपयोग करते हुए सावधान रहें-1 कोण को खोजने के लिए कार्य करते हैं, क्योंकि यह केवल पहले और चौथे क्वाड्रंट (–90 °) में लौटने वाले कोणों तक ही सीमित हैφ<90 °)।
जबसे z1 समन्वय प्रणाली के पहले चतुर्थांश में स्थित है, गणना है:
α 1 = तन-1(48 / 12) = टैन-1(4) = 75.96 °
जबसे z4 समन्वय प्रणाली के तीसरे चतुर्थांश में स्थित है, तन-1कोण को सही तरीके से नहीं लौटाता है। कोण गणना है:
α 4 = 180 ° + 75.96 ° = 255.96 ° या -360 ° + 255.96 ° = - 104.04 °, जो टीना द्वारा गणना के समान है।
z2 समन्वय प्रणाली के चौथे चतुर्थांश में स्थित है कोण गणना है:
α 2 = तन-1(-48 / 12) = टैन-1(-4) = -75.96 °
z3, हालाँकि, समन्वय प्रणाली के 2nd चतुर्थांश में है, इसलिए तन-1 कोण को सही ढंग से वापस नहीं करता है। कोण गणना है:
α 3 = 180 ° -75.96 ° = 104.04 °।
उदाहरण 4 हमारे पास दो जटिल संख्याएँ हैं: z1= 4 - j 6 और z2 = एक्सएनयूएमएक्स ईj45 ° .
खोज z3 = z1 + z2; z4 = z1 - z2; z5 = z1 * z2; z6 = z1 / z2
पहले हम टीना के इंटरप्रेटर का उपयोग करके समस्या का समाधान करते हैं
{टीना के दुभाषिया द्वारा समाधान} |
ध्यान दें कि विभिन्न रूपों में दी गई दो जटिल संख्याओं को टीना सहजता से कैसे संभालती है।
दुभाषिया के बिना समाधान अधिक जटिल है। ताकि हम गुणन और विभाजन के विभिन्न तरीकों की तुलना कर सकें, हम पहले ध्रुवीय रूप का निर्धारण करेंगे z1 और का आयताकार रूप z2 .
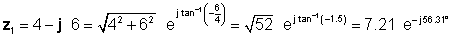
अगला, हम पहले सबसे आसान रूपों का उपयोग करके चार समाधान पाते हैं: जोड़ और घटाव के लिए आयताकार, और गुणन और विभाजन के लिए घातांक:
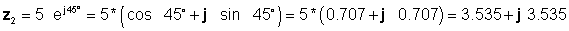
z 3 = z1 + z2 = 4 - j 6 + 3.535 + j 3.535 = 7.535 - j2.465
z 4 = z1 - z2 = 4 - j 6 - 3.535 - j 3.535 = 0.465 - j9.535
z 5 = z1 * z2 = 7.21 * 5 * ej(56.31 ° + 45 °) = एक्सएनयूएमएक्स ई -j11.31 ° = 36.03 * (cos -11.31 °) +j* पाप (-11.31 °))
z 5 = 35.33 - j 7.07
z 6 = z1/z2= (7.21 / 5) * ई j (56.31 ° -45 °) = एक्सएनयूएमएक्स ई - j 101.31 ° = 1.442 (cos (-101.31 °) +j* पाप (-101.31 °))
z 6 = -0.2828 - j 1.414
जो टीना दुभाषिया के साथ प्राप्त परिणामों से सहमत हैं।
आयताकार रूप में किया गया गुणन:
z 5 =z1*z2 = (4-j6) * 3.535 * (1 +j) = 7.07 * (2-j3) * (1 +j) = 7.07 * (2-j3+j2 + 3) = 7.07 * (5-j) = 35.35-j7.07
अंत में विभाजन आयताकार रूप में किया गया:
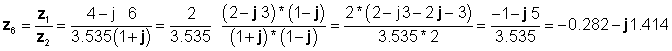
जो पिछले परिणामों से सहमत हैं।

