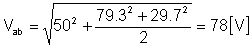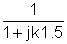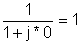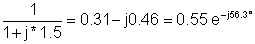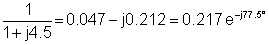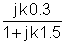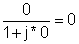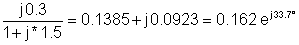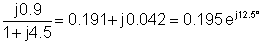အွန်လိုင်းသူတို့ကို Analyze မှ TINACloud မြွက်နှင့် Interactive မှ DC က mode ကို select လုပ်ဖို့အောက်ကဥပမာဆားကစ်ကိုကလစ်နှိပ်ပါသို့မဟုတ်ထိပုတ်ပါ။
အွန်လိုင်းသူတို့ကို Analyze မှ TINACloud မြွက်နှင့် Interactive မှ DC က mode ကို select လုပ်ဖို့အောက်ကဥပမာဆားကစ်ကိုကလစ်နှိပ်ပါသို့မဟုတ်ထိပုတ်ပါ။ ဥပမာတည်းဖြတ်သို့မဟုတ်သင့်ကိုယ်ပိုင်ဆားကစ်ကိုဖန်တီးရန် TINACloud တစ်ဦးအနိမ့်ကုန်ကျစရိတ်လက်လှမ်း Get
အဆိုပါ Fourier theorem မဆို Periodic လှိုင်းပုံစံအမျိုးမျိုးသောကြိမ်နှုန်း၏သင့်လျော်စွာအလေးချိန် sine နှင့် cosine အသုံးအနှုန်းများထည့်သွင်းခြင်းဖြင့်ဖန်တီးနိုင်ပါတယ်ကြောင်းဖော်ပြသည်။ Theorem သည်အခြားဖတ်စာအုပ်များတွင်ကောင်းစွာဖုံးလွှမ်းထားသဖြင့်ရလဒ်များကိုအတိုချုပ်ဖော်ပြပြီးသာဓကအချို့ကိုပြသလိမ့်မည်။
ကျွန်ုပ်တို့၏ Periodic function ကို f (t) = f (t ကို) ကြကုန်အံ့ ±T) သည် T တစ်ခု၏အချိန်ကာလဖြစ်ပြီး n သည်ကိန်းပြည့်ဖြစ်သည်။
w0= 2p/ T က အခြေခံ angular ကြိမ်နှုန်း။
က Fourier theorem, Periodic function ကိုအောက်ပါပေါင်းလဒ်အဖြစ်ရေးနိုင်သည်။
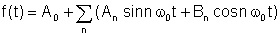
ဘယ်မှာ 
An နှင့် Bn အဆိုပါများမှာ Fourier ကိန်း နှင့်ပေါင်းလဒ်အတွက်ဖြစ်ပါသည် Fourier စီးရီး.
အခြားပုံစံတစ်ခုဖြစ်ပြီးနည်းနည်း ပို၍ လက်တွေ့ကျနိုင်သည်။
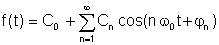
ဘယ်မှာ
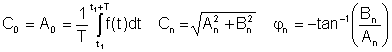
A0 = ကို C0 DC သည်သို့မဟုတ်ပျမ်းမျှတန်ဖိုး A ဖြစ်သည်1, B,1 နှင့် C1 အခြေခံကျသောအစိတ်အပိုင်းများဖြစ်ပြီး, အခြားသူများသဟဇာတအသုံးအနှုန်းများဖြစ်ကြသည်။
အချို့သောအသုံးအနှုန်းများသည်အချို့သောလှိုင်းပုံစံများကိုခန့်မှန်းရန်လိုအပ်သော်လည်းအချို့မှာအသုံးအနှုန်းများစွာလိုအပ်သည်။
ယေဘူယျအားဖြင့်စကားလုံးများများများထည့်သွင်းလေပိုမိုနီးကပ်လာလေလေစတုဂံလှုံ့ဆော်မှုများကဲ့သို့သောလှိုင်းပုံစံများအတွက် Gibbs ဖြစ်ရပ်ဆန်း ကစားသို့ကြွလာ။ ဝေါဟာရများများများတိုးများလာသည်နှင့်အမျှ overshoot ကို ပို၍ သေးငယ်သည့်အချိန်ကာလတစ်ခုအတွင်းတွင်သာစုစည်းမိသည်။
An ပင် function ကို f (t) = f (-t) (ဝင်ရိုး symmetry) သည်cosာဝေါဟာရများသာလိုအပ်သည်။
An ထူးဆန်း function ကို f (t) = - f (-t) (point symmetry) သည် sine term များသာလိုအပ်သည်။
အတူတစ်ဦးက waveform မှန်သို့မဟုတ်ဝက်လှိုင်း symmetry သာရှိပါတယ် ထူးဆန်းသော ယင်း၏ Fourier ကိုယ်စားပြုမှုအတွက်သဟဇာတ။
ဤနေရာတွင် Fourier စီးရီးတိုးချဲ့မှုကိုကျွန်ုပ်တို့ကိုင်တွယ်လိမ့်မည်မဟုတ်ပါ၊ သို့သော်၎င်းကိုပေးထားသော sines နှင့် cosine ပေါင်းလဒ်ကိုတိုက်နယ်တစ်ခုအတွက်စိတ်လှုပ်ရှားစရာအဖြစ်သာအသုံးပြုပါမည်။
ဤစာအုပ်၏အစောပိုင်းအခန်းကြီးများတွင်ကျွန်ုပ်တို့သည် sinusoidal စိတ်လှုပ်ရှားမှုကိုကိုင်တွယ်ဖြေရှင်းခဲ့သည်။ အကယ်၍ circuit သည် linear ဖြစ်ပါက၊ superposition ဖြစ်လာတယ် theorem တရားဝင်သည် nonsinusoidal Periodic စိတ်လှုပ်ရှားမှုနှင့်အတူကွန်ယက်အတွက်, superposition ကျွန်တော်တို့ကိုခွင့်ပြုပါတယ် တစ်ခုချင်းစီကို Fourier sinusoid သက်တမ်းတစ်ခုကြောင့်ကြောင့်ရေစီးကြောင်းနှင့် voltages ကိုတွက်ချက်။ အားလုံးတွက်ချက်သောအခါ, နောက်ဆုံးတော့ကျနော်တို့တုန့်ပြန်၏သဟဇာတအစိတ်အပိုင်းများကိုအကျဉ်းချုပ်။
Periodic voltage နှင့် current မ်ား၏မတူညီသောစည်းမျဉ်းများကိုဆုံးဖြတ်ရန်မှာအနည်းငယ်ရှုပ်ထွေးပြီး၊ အချက်အလက်များအလွန်အကျွံထုတ်လွှတ်နိုင်သည်။ လက်တွေ့တွင်တိုင်းတာမှုများလုပ်လိုသည်။ မတူညီသောသဟဇာတဝေါဟာရများကို a ကို အသုံးပြု၍ တိုင်းတာနိုင်သည် သဟဇာတ Analyzer, လှိုင်းခွဲခြမ်းစိတ်ဖြာသို့မဟုတ် Fourier ခွဲခြမ်းစိတ်ဖြာ။ ဤသူအပေါင်းတို့သည်များမှာ ရှုပ်ထွေးပြီးဖြစ်ကောင်းလိုအပ်သောထက်ပိုမိုဒေတာလိုက်လျော။ တစ်ခါတစ်ရံတွင်၎င်းသည်ပျမ်းမျှတန်ဖိုးများဖြင့်သာ Periodic signal ကိုဖော်ပြရန်လုံလောက်ပါသည်။ သို့သော်ပျှမ်းမျှတိုင်းတာမှုအမျိုးမျိုးရှိသည်။
ပျမ်းမျှ အဘိုး
ရိုးရှင်းသောပျှမ်းမျှ or DC အသုံးအနှုန်းကို Fourier ကိုယ်စားပြုမှုကို A အဖြစ်ရှုမြင်ခဲ့သည်0
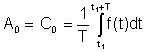
ဤပျမ်းမျှအား Deprez ကဲ့သို့သောတူရိယာများဖြင့်တိုင်းတာနိုင်သည် DC ကတူရိယာ။
ထိရောက်သောတန်ဖိုးကို or RMS အ (root mean square) တွင်အောက်ပါအဓိပ္ပါယ်ဖွင့်ဆိုချက်ရှိသည် -
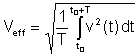
ဤသည်မှာအရေးကြီးဆုံးပျမ်းမျှတန်ဖိုးဖြစ်သည်။ အဘယ်ကြောင့်ဆိုသော် resistors များအတွင်းရှိအပူပျောက်သွားခြင်းသည်ထိရောက်သောတန်ဖိုးနှင့်အချိုးကျသောကြောင့်ဖြစ်သည်။ များစွာသော digital နှင့်အချို့သော analog voltmeter များသည် voltage နှင့် current တို့၏တန်ဖိုးကိုတိုင်းတာနိုင်သည်။
အကြွင်းမဲ့အာဏာပျှမ်းမျှ
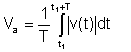
ဒီပျှမ်းမျှမရှိတော့ဘူး၊ အစောပိုင်းကတူရိယာပျမ်းမျှ၏ဤပုံစံကိုတိုင်းတာသည်။
အကယ်၍ ကျွန်ုပ်တို့သည် voltage သို့မဟုတ် current waveform ၏ Fourier ကိုယ်စားပြုမှုကိုသိရှိပါကကျွန်ုပ်တို့သည်ပျမ်းမျှတန်ဖိုးများကိုအောက်ပါအတိုင်းတွက်ချက်နိုင်သည်။
ရိုးရှင်းသောပျှမ်းမျှ or DC အသုံးအနှုန်းကို Fourier ကိုယ်စားပြုမှုကို A အဖြစ်ရှုမြင်ခဲ့သည်0 = ကို C0
ထိရောက်သောတန်ဖိုးကို or RMS အ (root mean square) သည် voltage ၏ Fourier စီးရီးများကိုပေါင်းစပ်ပြီးနောက်ဖြစ်သည်။
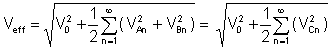
အဆိုပါ klirr အချက် ပျှမ်းမျှတန်ဖိုးများ၏အလွန်အရေးကြီးသောအချိုးသည်
၎င်းသည်ပိုမိုမြင့်မားသောသဟဇာတအသုံးအနှုန်းများ၏ထိရောက်သောတန်ဖိုးအချိုးဖြစ်သည် အခြေခံသဟဇာတ၏ထိရောက်သောတန်ဖိုးကိုရန်:
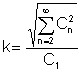

ဤနေရာတွင်ဆန့်ကျင်မှုများရှိပုံရသည် - ကျွန်ုပ်တို့သည်သဟဇာတဖြစ်သောအစိတ်အပိုင်းများအရကွန်ယက်ကိုဖြေရှင်းသည်၊ သို့သော်ကျွန်ုပ်တို့သည်ပျှမ်းမျှပမာဏကိုတိုင်းတာသည်။
ကျွန်တော်တို့ကိုရိုးရှင်းတဲ့ဥပမာအားဖြင့်နည်းလမ်းသရုပျဖျောကြစို့:
ဥပမာအား 1
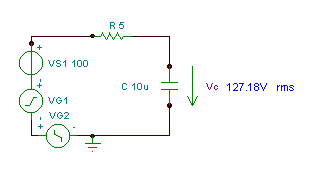
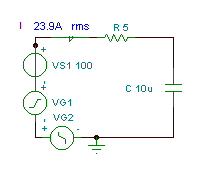
time function နှင့် voltage v ၏ထိရောက်သော (rms) တန်ဖိုးကိုရှာပါC(န)
R ကို = 5 အုမ်း, C ကို = 10 လျှင် mF နှင့် v (t) = (100 + 200 cos (w0t ကို) + 30 cos (3 w0t - 90 °)) V ကို, ထောင့်ကြိမ်နှုန်းအခြေခံရှိရာ w0= 30 / s ကို krad ။
ပြtheနာကိုဖြေရှင်းရန် superposition theorem ကိုသုံးပါ။
ပထမအဆင့်သည် transfer function ကို frequency ၏ function တစ်ခုအဖြစ်ရှာဖွေရန်ဖြစ်သည်။ ရိုးရိုးရှင်းရှင်းအဘို့, အစားထိုးကိုသုံးပါ: s = ည w
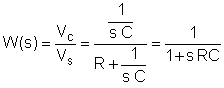
ယခုအစိတ်အပိုင်းတန်ဖိုးများနှင့် s = jk အစားထိုး w0ဘယ်မှာဋ = 0; 1; ဒီဥပမာမှာ 3 နှင့် w0= 30 krad / s နဲ့။ V ကို, တစ်ဦးက, အုမ်းအတွက် mF နှင့် Mrad / s ကိုယူနစ်:
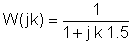
ကိန်းဂဏန်းဖြေရှင်းနည်း၏အဆင့်များကိုစုစည်းရန်ဇယားတစ်ခုကိုအသုံးပြုခြင်းသည်အထောက်အကူဖြစ်သည်။
k | W က (JK) = |
0 |
|
1 |
|
3 |
|
အခြားဇယားရှိ superposition ဖြေရှင်းချက်၏အဆင့်များကိုအတိုချုပ်ဖော်ပြနိုင်သည်။ ကျွန်ုပ်တို့တွေ့ခဲ့ရသည့်အတိုင်း၊ အစိတ်အပိုင်းတစ်ခု၏ရှုပ်ထွေးသောအထွတ်အထိပ်တန်ဖိုးကိုရှာဖွေရန်ကျွန်ုပ်တို့သည်စိတ်လှုပ်ရှားမှု၏အစိတ်အပိုင်း၏ရှုပ်ထွေးသောအထွတ်အထိပ်တန်ဖိုးကိုရှုပ်ထွေးသောလွှဲပြောင်း function ၏တန်ဖိုးဖြင့်မြှောက်သင့်သည်။:
k | V | W | VCk |
0 | 100 | 1 | 100 |
1 | 200 | 0.55e-j56.3° | 110e-j56.3° |
3 | 30e-j90° | 0.217e-j77.5° | 6.51e-j167.5° |
နောက်ဆုံးအနေဖြင့်ကျွန်ုပ်တို့သည်အစိတ်အပိုင်းများ၏ရှုပ်ထွေးသောအထွတ်အထိပ်တန်ဖိုးများကို သိ၍ အချိန် function ကိုပေးနိုင်သည်။
vC(t) = 100 + 110 cos (w0t - 56.3°) + 6.51 cos (3w0t - 167.5°) V
ဗို့အား၏ rms (ထိရောက်သော) တန်ဖိုးသည်
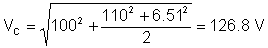
သင်မြင်သည့်အတိုင်း TINA ၏တိုင်းတာကိရိယာသည်ဤ rms တန်ဖိုးကိုတိုင်းတာသည်။
ဥပမာအား 2
time function နှင့်လက်ရှိ i (t) ၏ထိရောက်သော (rms) တန်ဖိုးကိုရှာပါ။
R ကို = 5 အုမ်း, C ကို = 10 လျှင် mF နှင့် v (t) = (100 + 200 cos (w0t ကို) + 30 cos (3w0t - 90 °)) အခြေခံ angular ကြိမ်နှုန်းသည်အဘယ်မှာရှိ V ကို w0= 30 / s ကို krad ။
ပြpositionနာကို superposition theorem ကို အသုံးပြု၍ ဖြေရှင်းရန်ကြိုးစားပါ။
  |
ဖြေရှင်းချက်အဆင့်များသည်ဥပမာ ၁ နှင့်ဆင်တူသော်လည်းလွှဲပြောင်းမှု function သည်ကွဲပြားခြားနားသည်။
အခုကိန်းဂဏန်းတန်ဖိုးများနှင့် s = jk ကိုအစားထိုး w0,ဘယ်မှာဋ = 0; 1; ဒီဥပမာမှာ 3 ။
V ကို, တစ်ဦးက, အုမ်းအတွက် mF နှင့် Mrad / s ကိုယူနစ်:
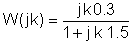
ကိန်းဂဏန်းဖြေရှင်းနည်းတွင်စားပွဲတစ်လုံးကိုသုံးခြင်းသည်အသုံးဝင်သည်။
k | W က (JK) = |
0 | |
1 | |
3 | |
အခြားဇယားရှိ superposition ၏အဆင့်များကိုအတိုချုပ်ဖော်ပြနိုင်သည်။ ကျွန်ုပ်တို့တွေ့ခဲ့ရသည့်အတိုင်း၊ အစိတ်အပိုင်းတစ်ခု၏အမြင့်ဆုံးတန်ဖိုးကိုရှာဖွေရန်ကျွန်ုပ်တို့သည်စိတ်လှုပ်ရှားမှု၏အစိတ်အပိုင်း၏ရှုပ်ထွေးသောအထွတ်အထိပ်တန်ဖိုးကိုရှုပ်ထွေးသောလွှဲပြောင်း function ၏တန်ဖိုးဖြင့်မြှောက်သင့်သည်။ စိတ်လှုပ်ရှားမှု၏အစိတ်အပိုင်းများ၏ရှုပ်ထွေးသောအထွတ်အထိပ်တန်ဖိုးများကိုအသုံးပြုပါ။
k | VSk | W(JK) | Ik |
0 | 100 | 0 | 0 |
1 | 200 | 0.162 ငj33.7° | 32.4 ငj33.7° |
3 | 30 င-j90° | 0.195 ငj12.5° | 5.85 င-j77.5° |
နောက်ဆုံးအနေဖြင့်အစိတ်အပိုင်းများ၏ရှုပ်ထွေးသောအထွတ်အထိပ်တန်ဖိုးများကိုသိရှိခြင်းဖြင့်ကျွန်ုပ်တို့သည်အချိန်လုပ်ဆောင်ချက်ကိုဖော်ပြနိုင်သည်။
ဈ (t) = 32.4 cos (w0t + 33.7°) + 5.85 cos (3w0t - 77.5°) [တစ်]
Tသူကလက်ရှိတန်ဖိုးကို rms:
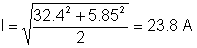
သင်မကြာခဏဖြေရှင်းချက်၏အစိတ်အပိုင်းတစ်ခုအဘို့အစိတ်ဖောက်ပြန်စစ်ဆေးမှုများလုပ်နိုင်ပါတယ်။ ဥပမာ capacitor တွင် DC voltage ရှိနိုင်သော်လည်း DC current မရှိပါ။
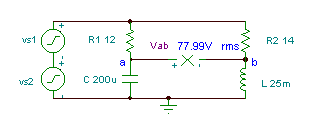
ဥပမာအား 3
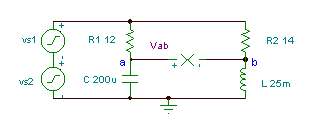
ဗို့ V ၏အချိန် function ကိုရယူပါab if R1= 12 အုမ်း, R ကို2 = 14 ohm, L ကို = 25 mH နှင့်
ကို C = 200 mအက်ဖ်မီးစက်ဗို့အား v (t) = (50 + 80 cos (w0t ကို) + 30 cos (2 w0t + 60 °)) V ကို, အခြေခံအကြိမ်ရေ, f သည်အဘယ်မှာရှိ0 = 50 Hz ။
ပထမအဆင့်မှာ transfer function ကိုရှာဖွေရန်ဖြစ်သည်။
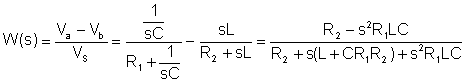
ကိန်းဂဏန်းတန်ဖိုးများကို V၊ A, ohm, mH, mF, kHz ယူနစ်များဖြင့်အစားထိုးသည် -
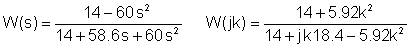
ကျောက်ပြားနှစ်ပြားပေါင်းခြင်း:
| ဋ V ကို Sk |   | V abk |
|---|---|---|
| 0 50 |   | 50 |
| 1 80 |   | 79.3 င-j66.3 |
| 2 30 ငj60 |   | 29.7 င-j44.7 |
နောက်ဆုံးအနေနဲ့ time function:
vab(t) = 50 + 79.3 cos (w1t - 66.3°) + 29.7 cos (2w1t - 44.7°) [V ကို]
နှင့် rms တန်ဖိုး: