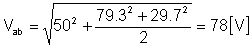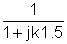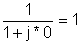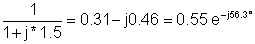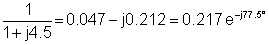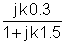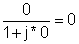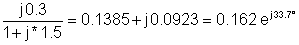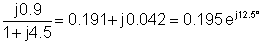Haga clic o toque los circuitos de ejemplo a continuación para invocar TINACloud y seleccione el modo DC interactivo para analizarlos en línea.
Obtenga un acceso de bajo costo a TINACloud para editar los ejemplos o crear sus propios circuitos

La Teorema de Fourier afirma que cualquier forma de onda periódica se puede sintetizar sumando términos seno y coseno ponderados adecuadamente de varias frecuencias. El teorema está bien tratado en otros libros de texto, por lo que solo resumiremos los resultados y mostraremos algunos ejemplos.

Sea nuestra función periódica f (t) = f (t ±nT) donde T es el tiempo de un período y n es un número entero.

w₀= 2p/ T la frecuencia angular fundamental.

Por el Teorema de Fourier, la función periódica se puede escribir como la siguiente suma:

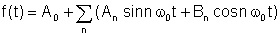
donde

A_n y B_n son los Coeficientes de Fourier y la suma es la series de Fourier.

Otra forma, probablemente un poco más práctica:

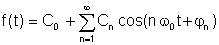
donde

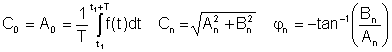
A₀ = C₀ es el DC o valor promedio, A₁, B₁ y C₁ son los componentes fundamentales, y los demás son los términos armónicos.

Si bien es posible que solo se requieran unos pocos términos para aproximar algunas formas de onda, otras requerirán muchos términos.

Generalmente, cuantos más términos se incluyan, mejor será la aproximación, pero para las formas de onda que contienen pasos, como los impulsos rectangulares, la Fenómeno de Gibbs entra en juego. A medida que aumenta el número de términos, el exceso se concentra en un período de tiempo cada vez más pequeño.

An Incluso función f(t) = f(-t) (simetría del eje) requiere sólo términos cosenos.

An Función impar f(t) = – f(-t) (simetría puntual) requiere sólo términos sinusoidales.

Una forma de onda con simetría de espejo o de media onda Sólo tiene odd armónicos en su representación de Fourier.

Aquí no nos ocuparemos del desarrollo en serie de Fourier, sino que solo usaremos una suma dada de senos y cosenos como excitación para un circuito.

En los capítulos anteriores de este libro nos ocupamos de la excitación sinusoidal. Si el circuito es lineal, la teorema de superposición es válida. Para una red con excitación periódica no sinusoidal, la superposición nos permite Calcule las corrientes y voltajes debidos a cada término sinusoide de Fourier, uno a la vez. Cuando todos están calculados, finalmente resumimos los componentes armónicos de la respuesta.

Es un poco complicado determinar los diferentes términos de las tensiones y corrientes periódicas y, de hecho, puede producir una sobrecarga de información. En la práctica nos gustaría simplemente realizar mediciones. Podemos medir los diferentes términos armónicos usando un analizador de armónicos, analizador de espectro, analizador de ondas o analizador de Fourier. Todos estos son complicado y probablemente proporcione más datos de los necesarios. A veces es suficiente describir una señal periódica sólo por sus valores medios. Pero existen varios tipos de medidas promedio.

PROMEDIO VALORES

Promedio simple or DC término fue visto en la representación de Fourier como A₀

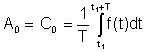
Este promedio se puede medir con instrumentos como el Deprez. Instrumentos de corriente continua.

Valor efectivo or rms (raíz cuadrática media) tiene la siguiente definición:

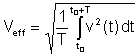
Este es el valor medio más importante porque el calor disipado en las resistencias es proporcional al valor efectivo. Muchos voltímetros digitales y algunos analógicos pueden medir el valor efectivo de voltajes y corrientes.

Media absoluta

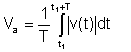
Este promedio ya no es importante; instrumentos anteriores medían esta forma de promedio.

Si conocemos la representación de Fourier de una forma de onda de voltaje o corriente, también podemos calcular los valores promedio de la siguiente manera:

Promedio simple or DC término fue visto en la representación de Fourier como A₀ = C₀

Valor efectivo or rms (media cuadrática) es, después de integrar la serie de Fourier del voltaje:

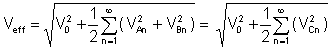
La factor klirr es una relación muy importante de los valores medios:

Es la relación del valor efectivo de los términos armónicos superiores. al valor efectivo del armónico fundamental:

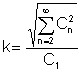
Parece haber una contradicción aquí: resolvemos la red en términos de componentes armónicos, pero medimos cantidades promedio.

Ilustremos el método con ejemplos simples:

Ejemplo 1

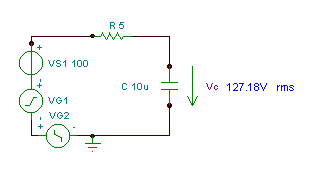
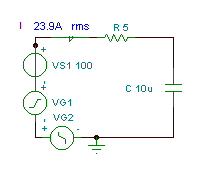
Encuentre la función de tiempo y el valor efectivo (rms) del voltaje v_C(T)

si R = 5 ohm, C = 10 mF y v (t) = (100 + 200 cos (w₀t) + 30 cos (3 w₀t - 90 °)) V, donde la frecuencia angular fundamental es w₀= 30 krad / s.

Intenta usar el teorema de superposición para resolver el problema.

El primer paso es encontrar la función de transferencia en función de la frecuencia. Para simplificar, utilice la sustitución: s = j w

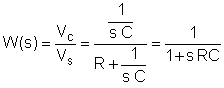
Ahora sustituya los valores de los componentes y s = jk w₀donde k = 0; 1; 3 en este ejemplo y w₀= 30 krad/s. En V, A, ohm, mUnidades F y Mrad / s:

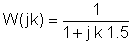
Es útil utilizar una tabla para organizar los pasos de la solución numérica:

Podemos resumir los pasos de la solución de superposición en otra tabla. Como ya hemos visto, para encontrar el valor pico complejo de un componente, debemos multiplicar el valor pico complejo del componente de excitación por el valor de la función de transferencia compleja.:

Y finalmente podemos dar la función de tiempo conociendo los valores pico complejos de los componentes:

v_C(t) = 100 + 110 cos(w₀t - 56.3°) + 6.51 cos (3w₀t - 167.5°) V

El valor rms (efectivo) del voltaje es:

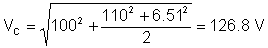
Como puede ver, el instrumento de medición de TINA mide este valor rms.

ejemplo 2

Encuentre la función de tiempo y el valor efectivo (rms) de la corriente i(t)

si R = 5 ohm, C = 10 mF y v (t) = (100 + 200 cos (w₀t) + 30 cos (3w₀t - 90 °)) V donde la frecuencia angular fundamental es w₀= 30 krad / s.

Intenta resolver el problema usando el teorema de superposición.

Los pasos de la solución son similares al Ejemplo 1, pero la función de transferencia es diferente.

Ahora sustituye los valores numéricos y s = jk w_0,donde k = 0; 1; 3 en este ejemplo.

En V, A, ohm, mUnidades F y Mrad / s:

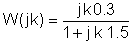
Es útil utilizar una tabla durante la solución numérica:

Podemos resumir los pasos de la superposición en otra tabla. Como ya hemos visto, para encontrar el valor pico de un componente, debemos multiplicar el valor pico complejo de ese componente de la excitación por el valor de la función de transferencia compleja. Utilice los valores máximos complejos de los componentes de la excitación:

Y finalmente, conociendo los valores pico complejos de los componentes podemos enunciar la función del tiempo:

i (t) = 32.4 cos (w₀t + 33.7°) + 5.85 cos (3w₀t - 77.5°) [UN]

TEl valor eficaz de la corriente:

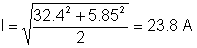
A menudo puedes hacer una verificación de cordura para parte de la solución. Por ejemplo, un condensador puede tener un voltaje CC pero no una corriente CC.

ejemplo 3

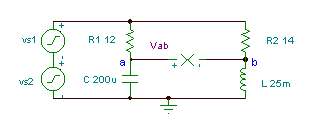
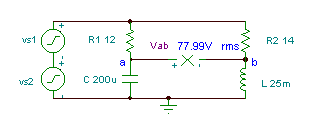
Obtener la función del tiempo del voltaje V._ab if R₁= 12 ohm, R₂ = 14 ohmios, L = 25 mH, y

C = 200 mF. El voltaje del generador es v(t)=(50 + 80 cos(w₀t) + 30 cos (2 w₀t + 60 °)) V, donde la frecuencia fundamental es f₀ = 50 Hz.

El primer paso es encontrar la función de transferencia:

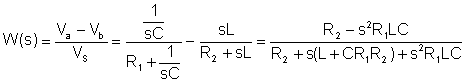
Sustitución de valores numéricos en unidades V, A, ohm, mH, mF, kHz:

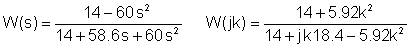
Fusionando las dos tablas:

k V Sk		V abk
0 50		50
1 80		79.3 correo-j66.3
2 30 ej60		29.7 correo-j44.7

Finalmente la función de tiempo:

v_ab(t) = 50 + 79.3 cos (w₁t - 66.3°) + 29.7 cos (2w₁t - 44.7°) [V]

y el valor rms:

---