Haga clic o toque los circuitos de ejemplo a continuación para invocar TINACloud y seleccione el modo DC interactivo para analizarlos en línea.
Haga clic o toque los circuitos de ejemplo a continuación para invocar TINACloud y seleccione el modo DC interactivo para analizarlos en línea. Obtenga un acceso de bajo costo a TINACloud para editar los ejemplos o crear sus propios circuitos
Un voltaje sinusoidal puede ser descrito por la ecuación:
v (t) = VM sin (ωt + Φ) o v (t) = VM cos (ωt + Φ)
| donde | Vermont) | Valor instantáneo de la tensión, en voltios (V). |
| VM | Valor máximo o máximo del voltaje, en voltios (V) | |
| T | Período: El tiempo tomado para un ciclo, en segundos | |
| f | Frecuencia: el número de períodos en 1 segundo, en Hz (Hertz) o 1 / s. f = 1 / T | |
| ω | Frecuencia angular, expresada en radianes / s. ω = 2 * π * f o ω = 2 * π / T. | |
| Φ | Fase inicial dada en radianes o grados. Esta cantidad determina el valor de la onda senoidal o coseno att = 0. | |
| Nota: la amplitud de una tensión sinusoidal a veces se expresa como VEf, el valor efectivo o RMS. Esto está relacionado con VM segun la relacion vM= √2VEf o aproximadamente VEf = 0.707 VM |
Aquí hay algunos ejemplos para ilustrar los términos anteriores.
Las propiedades de la tensión de CA 220 V en tomas de corriente domésticas en Europa:
Valor efectivo: VEf = 220 V
Valor máximo: VM= √2 * 220 V = 311 V
Frecuencia: f = 50 1 / s = 50 Hz
Frecuencia angular: ω = 2 * π * f = 314 1 / s = 314 rad / s
Período: T = 1 / f = 20 ms
Función de tiempo: v (t) = 311 sin (314 t)
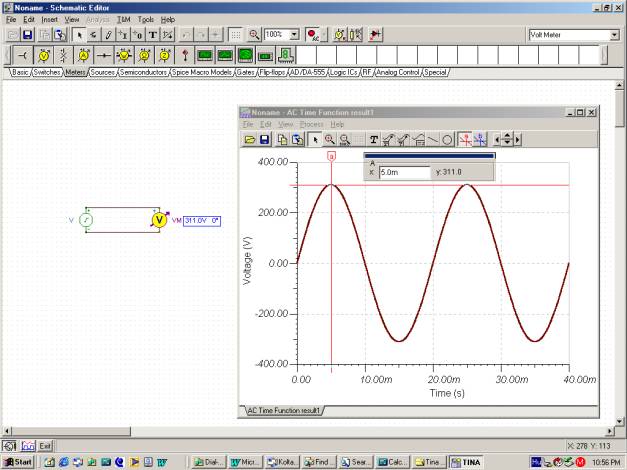
Veamos la función de tiempo usando el comando Análisis / Análisis de CA / Función de tiempo de TINA.
Puedes comprobar que el período es T = 20m y que VM = 311 V.
Las propiedades de la tensión de CA de 120 V en la toma de corriente doméstica en los Estados Unidos:
Valor efectivo: VEf = 120 V
Valor máximo: VM= √2 120 V = 169.68 V ≈ 170 V
Frecuencia: f = 60 1 / s = 60 Hz
Frecuencia angular: ω = 2 * π * f = 376.8 rad / s ≈ 377 rad / s
Período: T = 1 / f = 16.7 ms
Función de tiempo: v (t) = 170 sin (377 t)
Tenga en cuenta que, en este caso, la función de tiempo podría darse como v (t) = 311 sin (314 t + Φ) o v (t) = 311 cos (314 t + Φ), ya que en el caso de la tensión de salida No se conoce la fase inicial.
La fase inicial juega un papel importante cuando varios voltajes están presentes simultáneamente. Un buen ejemplo práctico es el sistema trifásico, donde están presentes tres voltajes del mismo valor pico, forma y frecuencia, cada uno de los cuales tiene un desplazamiento de fase de 120 ° en relación con los demás. En una red 60 Hz, las funciones de tiempo son:
vA(t) = 170 sin (377 t)
vB(t) = 170 sen (377 t - 120 °)
vC(t) = 170 sin (377 t + 120 °)
La siguiente figura hecha con TINA muestra el circuito con estas funciones de tiempo como generadores de voltaje de TINA.
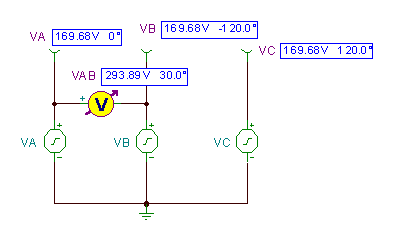

La diferencia de voltaje vAB= vA(TVB(t) se muestra como se resuelve con el comando Análisis / Análisis de CA / Función de tiempo de TINA.
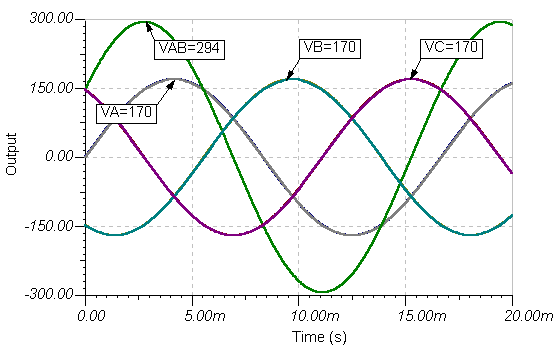

Tenga en cuenta que el pico de vAB (t) es aproximadamente 294 V, más grande que los picos 170 V de la vA(t) o vB(t) voltajes, pero también no simplemente la suma de sus voltajes pico. Esto se debe a la diferencia de fase. Vamos a discutir cómo calcular el voltaje resultante (que es Ö* 3 170 @ 294 en este caso) más adelante en este capítulo y también en el apartado Sistemas trifásicos .
Valores característicos de las señales sinusoidales.
Aunque una señal de CA varía continuamente durante su período, es fácil definir unos pocos valores característicos para comparar una onda con otra: Estos son los valores de pico, promedio y media cuadrática (rms).
Ya hemos alcanzado el valor máximo VM , que es simplemente el valor máximo de la función de tiempo, la amplitud de la onda sinusoidal.
A veces se usa el valor pico a pico (pp). Para voltajes y corrientes sinusoidales, el valor pico a pico es el doble del valor pico.
La valor promedio de la onda sinusoidal es el promedio aritmético de los valores para el semiciclo positivo. También es llamado promedio absoluto ya que es el mismo que el promedio del valor absoluto de la forma de onda. En la práctica, nos encontramos con esta forma de onda por rectificando La onda sinusoidal con un circuito llamado rectificador de onda completa.
Se puede mostrar que el promedio absoluto de una onda sinusoidal es:
VAV= 2 / π VM ≅ 0.637 VM
Tenga en cuenta que el promedio de un ciclo entero es cero.
El valor eficaz o efectivo de una tensión o corriente sinusoidal corresponde al valor de CC equivalente que produce la misma potencia de calefacción. Por ejemplo, un voltaje con un valor efectivo de 120 V produce la misma potencia de calefacción e iluminación en una bombilla que el 120 V de una fuente de voltaje de CC. Se puede mostrar que el valor eficaz o efectivo de una onda sinusoidal es:

Vrms V =M / √2 ≅ 0.707 VM
Estos valores se pueden calcular de la misma manera tanto para voltajes como para corrientes.
El valor rms es muy importante en la práctica. A menos que se indique lo contrario, los voltajes de CA de la línea de alimentación (por ejemplo, 110V o 220V) se dan en valores rms. La mayoría de los medidores de CA están calibrados en rms e indican el nivel de rms.
ejemplo 1 Encuentre el valor pico de la tensión sinusoidal en una red eléctrica con un valor de 220 V rms.
VM = 220 / 0.707 = 311.17 V
ejemplo 2 Encuentre el valor pico de la tensión sinusoidal en una red eléctrica con un valor de 110 V rms.
VM = 110 / 0.707 = 155.58 V
ejemplo 3 Encuentre el promedio (absoluto) de la tensión sinusoidal si su valor rms es 220 V.
Va = 0.637 * VM = 0.637 * 311.17 = 198.26 V
ejemplo 4 Encuentre el promedio absoluto de la tensión sinusoidal si su valor rms es 110 V.
El pico de la tensión del Ejemplo 2 es 155.58 V y por lo tanto:
Va = 0.637 * VM = 0.637 * 155.58 = 99.13 V
ejemplo 5 Encuentra la relación entre el promedio absoluto (Va) y valores rms (V) para la forma de onda sinusoidal.
V / Va = 0.707 / 0.637 = 1.11
Tenga en cuenta que no puede agregar valores promedio en un circuito de CA porque conduce a resultados incorrectos.
Los fasores
Como ya hemos visto en la sección anterior, a menudo es necesario en los circuitos de CA agregar voltajes sinusoidales y corrientes de la misma frecuencia. Aunque es posible agregar las señales numéricamente usando TINA, o empleando relaciones trigonométricas, es más conveniente usar las llamadas fasor Método. Un fasor es un número complejo que representa la amplitud y la fase de una señal sinusoidal. Es importante tener en cuenta que el fasor no representa la frecuencia, que debe ser la misma para todos los fasores.
Un fasor puede manejarse como un número complejo o representarse gráficamente como una flecha plana en el plano complejo. La representación gráfica se llama diagrama fasorial. Mediante los diagramas de fasores, puede sumar o restar fasores en un plano complejo mediante la regla de triángulo o paralelogramo.
Hay dos formas de números complejos: rectangular y polar.
La representación rectangular está en la forma +. jb, donde j = Ö-1 es la unidad imaginaria.
La representación polar está en la forma Ae.j j , donde A es el valor absoluto (amplitud) y f es el ángulo del fasor desde el eje real positivo, en sentido contrario a las agujas del reloj.
Usaremos Letras para cantidades complejas.
Ahora veamos cómo derivar el fasor correspondiente de una función de tiempo.
Primero, suponga que todos los voltajes en el circuito se expresan en forma de funciones de coseno. (Todos los voltajes se pueden convertir a esa forma). Luego el fasor correspondiente a la tensión de v (t) = VM cos w t+f) es: VM V =Me jf , que también se llama el valor pico complejo.
Por ejemplo, considere el voltaje: v (t) = 10 cos ( w t + 30°)
El fasor correspondiente es: 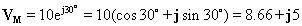
Podemos calcular la función de tiempo de un fasor de la misma manera. Primero escribimos el fasor en forma polar, por ejemplo. VM V =Me jr y luego la función de tiempo correspondiente es
v (t) = VM (coswt+r).
Por ejemplo, considere el fasor VM = 10 - j20 V
Llevándolo a la forma polar:
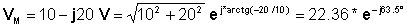
Y por lo tanto, la función de tiempo es: v (t) = 22.36 cos (wt - 63.5°) V
Los fasores se utilizan a menudo para definir el valor efectivo efectivo o rms de los voltajes y corrientes en los circuitos de CA. Dado v (t) = VMcoswt+r) = 10cos (wt + 30°)
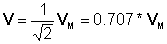
Numéricamente:
v (t) = 10 * cos (wt-30°)
El valor efectivo complejo (rms): V = 0.707 * 10 * e– j30° = 7.07 e– j30° = 6.13 - j 3.535
Viceversa: si el valor efectivo complejo de una tensión es:
V = - 10 + j 20 = 22.36 e j 116.5°
entonces el valor pico complejo: 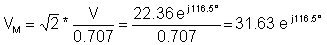
y la función de tiempo: v (t) = 31.63 cos ( wt + 116.5° ) V
Una breve justificación de las técnicas anteriores es la siguiente. Dada una función de tiempo
VM (cos w t+r), definamos la función de tiempo complejo como:
v (t) = VM e jr e jwt = VMe jwt V =M (cosr) + j pecado(r))mi jwt
donde VM =VM e j r t V =M (cosr) + j pecado(r)) es solo el fasor introducido anteriormente.
Por ejemplo, la función de tiempo complejo de v (t) = 10 cos (wt + 30°)
v (t) = VMe jwt = 10 e j30 e jwt = 10e jwt (cos (30) + j sin (30)) = e jwt (8.66 +j5)
Al introducir la función de tiempo complejo, tenemos una representación con una parte real y una parte imaginaria. Siempre podemos recuperar la función real original del tiempo tomando la parte real de nuestro resultado: v (t) = Re {v(t)}
Sin embargo, la función de tiempo complejo tiene la gran ventaja de que, dado que todas las funciones de tiempo complejas en los circuitos de CA en consideración tienen la misma ejwt multiplicador, podemos factorizar esto y simplemente trabajar con los fasores. Además, en la práctica no utilizamos la ejwt parte en absoluto - sólo las transformaciones de las funciones de tiempo a los fasores y viceversa.
Para demostrar la ventaja de usar fasores, veamos el siguiente ejemplo.
ejemplo 6 Encuentra la suma y la diferencia de los voltajes:
v1 = 100 cos (314 * t) y v2 = 50 cos (314 * t-45°)
Primero escribe los fasores de ambos voltajes:
V1M = 100 V2M= 50 e – j 45° = 35.53 - j 35.35
Por lo tanto:
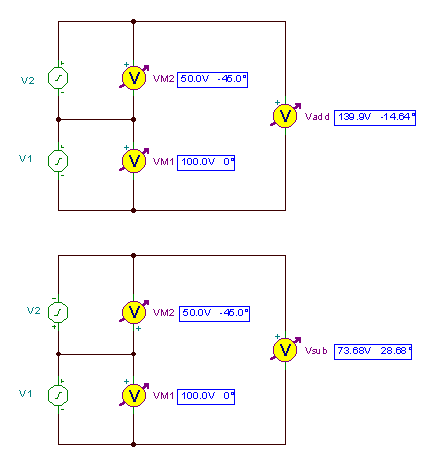
Vadd = V1M + V2M = 135.35 - j 35.35 = 139.89 e- j 14.63°
Vpor debajo = V1M – V2M = 64.65 + j35.35 = 73.68 correo j 28.67°
y luego el tiempo funciona:
vadd(t) = 139.89 * cos (wt - 14.63°)
vpor debajo(t) = 73.68 * cos (wt + 28.67°)
Como muestra este sencillo ejemplo, el método de los fasores es una herramienta extremadamente poderosa para resolver problemas de CA.
Resolvamos el problema usando las herramientas del intérprete de TINA.
{cálculo de v1 + v2}
v1: = 100
v2: = 50 * exp (-pi / 4 * j)
v2 = [35.3553-35.3553 * j]
v1add: = v1 + v2
v1add = [135.3553-35.3553 * j]
abs (v1add) = [139.8966]
radtodeg (arc (v1add)) = [- 14.6388]
{cálculo de v1-v2}
v1sub: = v1-v2
v1sub = [64.6447 + 35.3553 * j]
abs (v1sub) = [73.6813]
radtodeg (arc (v1sub)) = [28.6751]
#cálculo de v1+v2
importar matemáticas como m
importar cmath como c
v1=100
v2=50*c.exp(complejo(0,-c.pi/4))
imprimir(“v2=”,v2)
vadd=v1+v2
imprimir(“vadd=”,vadd)
imprimir(“abs(vadd)=”,abs(vadd))
print(“grados(arco(vadd))=”,m.grados(c.fase(vadd)))
#cálculo de v1-v2
vsub=v1-v2
imprimir(“vsub=”,vsub)
imprimir(“abs(vsub)=”,abs(vsub))
imprimir ("grados (arco (vsub)) =", m.grados (c.fase (vsub)))
Los resultados de amplitud y fase confirman los cálculos manuales.
Ahora veamos el resultado usando el análisis de CA de TINA.
Antes de realizar el análisis, asegurémonos de que Función base para AC se establece en coseno existentes Opciones del editor cuadro de diálogo del menú Ver / Opción. Vamos a explicar el papel de este parámetro en ejemplo 8.
Los circuitos y los resultados:
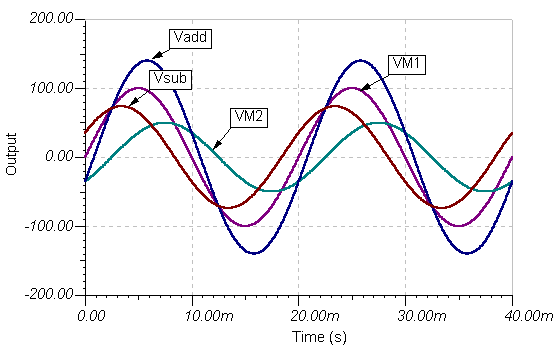
De nuevo el resultado es el mismo. Aquí están los gráficos de función de tiempo:
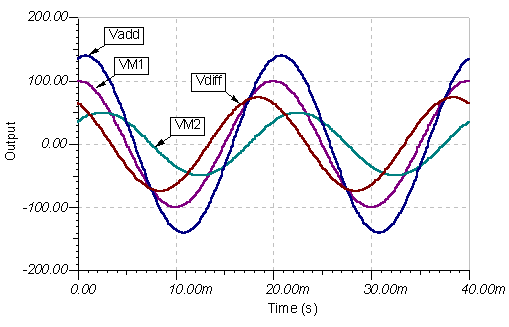
ejemplo 7 Encuentra la suma y la diferencia de los voltajes:
v1 = 100 sin (314 * t) y v2 = 50 cos (314 * t-45°)
Este ejemplo trae una nueva pregunta. Hasta ahora hemos requerido que todas las funciones de tiempo se den como funciones de coseno. ¿Qué haremos con una función de tiempo dada como senoidal? La solución es transformar la función seno a una función coseno. Usando la relación trigonométrica sin (x) = cos (x-p/ 2) = cos (x-90°), nuestro ejemplo se puede reformular de la siguiente manera:
v1 = 100 cos (314t - 90°) y v2 = 50 cos (314 * t - 45°)
Ahora los fasores de los voltajes son:
V1M = 100 e – j 90° = -100 j V2M= 50 e – j 45° = 35.53 - j 35.35
Por lo tanto:
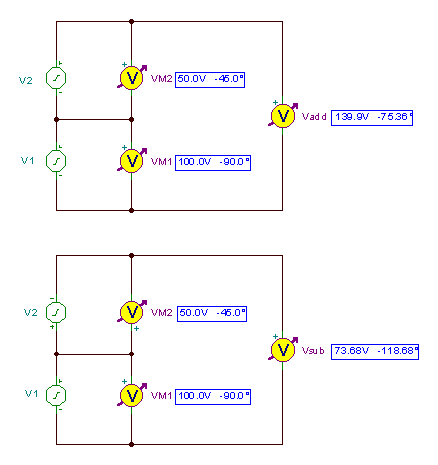
V add = V1M + V2M = 35.53 - j 135.35
V por debajo = V1M – V2M = - 35.53 - j 64.47
y luego el tiempo funciona:
vadd(t) = 139.8966 cos (wt-75.36°)
vpor debajo(t) = 73.68 cos (wt-118.68°)
Resolvamos el problema usando las herramientas del intérprete de TINA.
{cálculo de v1 + v2}
v1: = - 100 * j
v2: = 50 * exp (-pi / 4 * j)
v2 = [35.3553 - 35.3553 * j]
v1add: = v1 + v2
v1add = [35.3553-135.3553 * j]
abs (v1add) = [139.8966]
radtodeg (arc (v1add)) = [- 75.3612]
{cálculo de v1-v2}
v1sub: = v1-v2
v1sub = [- 35.3553 - 64.6447 * j]
abs (v1sub) = [73.6813]
radtodeg (arc (v1sub)) = [- 118.6751]
#cálculo de v1+v2
importar matemáticas como m
importar cmath como c
v1=100
v2=50*c.exp(complejo(0,-c.pi/4))
imprimir(“v2=”,v2)
vadd=v1+v2
imprimir(“vadd=”,vadd)
imprimir(“abs(vadd)=”,abs(vadd))
print(“grados(arco(vadd))=”,m.grados(c.fase(vadd)))
#cálculo de v1-v2
vsub=v1-v2
imprimir(“vsub=”,vsub)
imprimir(“abs(vsub)=”,abs(vsub))
imprimir ("grados (arco (vsub)) =", m.grados (c.fase (vsub)))
Veamos el resultado con el análisis de CA de TINA.
ejemplo 8
Encuentra la suma y la diferencia de los voltajes:v1 = 100 sin (314 * t) y v2 = 50 sin (314 * t-45°)
Este ejemplo trae un problema más. ¿Qué pasa si todos los voltajes se dan como ondas sinusoidales y también deseamos ver el resultado como una onda sinusoidal? Por supuesto, podríamos convertir ambos voltajes en funciones coseno, calcular la respuesta y luego convertir el resultado en una función seno, pero esto no es necesario. Podemos crear fasores a partir de las ondas sinusoidales de la misma manera que lo hicimos a partir de las ondas coseno y luego simplemente usar su amplitud y fases como amplitud y fase de las ondas sinusoidales en el resultado.
Obviamente, esto dará el mismo resultado que la transformación de las ondas sinusoidales en ondas de coseno. Como pudimos ver en el ejemplo anterior, esto es equivalente a multiplicar por -j y luego usando el cos (x) = sen (x-90)°) Relación para transformarlo de nuevo en una onda sinusoidal. Esto es equivalente a multiplicar por j. En otras palabras, desde -j × j = 1, podríamos usar los fasores derivados directamente de las amplitudes y fases de las ondas sinusoidales para representar la función y luego regresar a ellas directamente. Además, al razonar de la misma manera sobre las funciones de tiempo complejas, podríamos considerar las ondas sinusoidales como las partes imaginarias de las funciones de tiempo complejas y complementarlas con la función de coseno para crear la función de tiempo complejo completo.
Veamos la solución a este ejemplo usando las funciones seno como base de los fasores (transformando sin ( w t) a la unidad real de fasor (1)).
V1M = 100 V2M= 50 e – j 45° = 35.53 - j 35.35
Por lo tanto:
V add = V1M + V2M = 135.53 - j 35.35
V por debajo = V1M – V2M = 64.47+ j 35.35
Tenga en cuenta que los fasores son exactamente los mismos que en el Ejemplo 6 pero no las funciones de tiempo:
v3(t) = 139.9sin (wt 14.64 Mayo°)
v4(t) = 73.68sin (wt + 28.68°)
Como puede ver, es muy fácil obtener el resultado usando funciones sinusoidales, especialmente cuando nuestros datos iniciales son ondas sinusoidales. Muchos libros de texto prefieren utilizar la onda sinusoidal como función básica de los fasores. En la práctica, puede utilizar cualquiera de los métodos, pero no los confunda.
Cuando creas los fasores, es muy importante que todas las funciones de tiempo se conviertan primero en seno o coseno. Si comenzó desde las funciones sinusoidales, sus soluciones deberían representarse con funciones sinusoidales cuando regrese de los fasores a las funciones de tiempo. Lo mismo es cierto si comienzas con las funciones de coseno.
Resolvamos el mismo problema usando el modo interactivo de TINA. Ya que queremos usar las funciones de seno como la base para crear los fasores, asegúrese de que Función base para AC se establece a seno existentes Opciones del editor cuadro de diálogo del menú Ver / Opción.
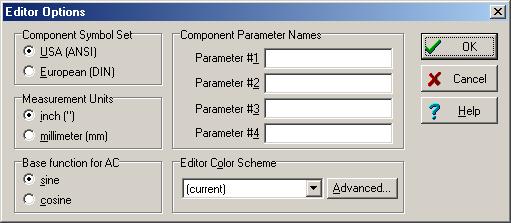

Los circuitos para hacer la suma y la diferencia de las formas de onda y el resultado:
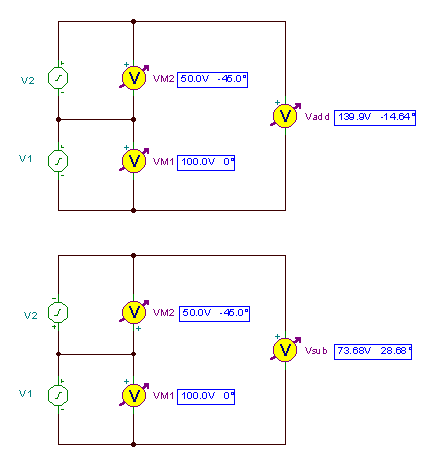
y las funciones de tiempo: