Egin klik beheko edo Idatzi beheko zirkuituak TINACloud deitzeko eta hautatu Lineako DC interaktiboa hautatzeko.
Egin klik beheko edo Idatzi beheko zirkuituak TINACloud deitzeko eta hautatu Lineako DC interaktiboa hautatzeko. Eskuratu TINACloud-era kostu txikia adibide horiek editatzeko edo zure zirkuituak sortzeko
Kirchhoff-en ekuazioen multzo osoa errazteko beste modu bat sare edo begizta korrontearen metodoa da. Metodo hau erabiliz, Kirchhoffen egungo legea automatikoki asetzen da eta idazten ditugun begien ekuazioek Kirchhoffen tentsio legea ere asetzen dute. Kirchhoffen egungo legea asetzea zirkuituaren begizta independente bakoitzari sare edo begizta korronte itxiak esleituz lortzen da eta korronte hauek zirkuituaren gainerako kantitate guztiak adierazteko. Begizta korronteak itxita daudenez, nodo batetik sartzen den korrontea ere nodoetatik atera behar da; beraz, korronte hauekin nodo ekuazioak idazteak identitatea dakar.
Azter ditzagun lehenik sareko korronteen metodoa.
Lehenik eta behin, sareko korrontearen metodoa zirkuitu "planetan" soilik aplikatzen dela nabaritzen dugu. Zirkuitu planoek hegazkin batean marraztutakoan ez dute zeharkatzeko haririk. Sarritan, plano ez den zirkuitua berriro marrazten baduzu, planoa dela egiazta dezakezu. Plano ez diren zirkuituetarako erabili begiztako uneko metodoa ondorengo atal honetan deskribatu da.
Sare-korronteen ideia azaltzeko, imajinatu zirkuituaren adarrak "arrantza-sare" gisa eta sareko sare bakoitzari sare bat eman. (Batzuetan, zirkuituaren "leiho" bakoitzean korronte itxi bat esleitzen dela ere esaten da.)
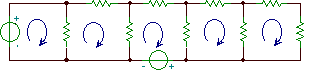  Eskemaren diagrama   "Arrantza-sarea" edo zirkuituaren grafikoa |
Zirkuitua marrazki soil baten bidez irudikatzeko teknika, a grafikoan, nahiko indartsua da. geroztik Kirchhoffen legeak ez dira osagaien izaeraren araberakoak, hormigoizko osagaiak baztertu eta lerro segmentu soilak ordezkatu ditzakezu adarrak grafikoa. Zirkuituak grafikoen bidez irudikatzeak matematikaren teknikak erabiltzea ahalbidetzen digu grafikoen teoria. Honek zirkuitu baten izaera topologikoa arakatzen eta begizta independenteak zehazten laguntzen digu. Itzuli gero gune honetara gai honi buruz gehiago irakurtzeko.
Uneko analisiaren sareko urratsak:
Esleitu sare korronte bat sare bakoitzari. Norabidea arbitrarioa izan arren, ohikoa da erloju orratzen norabidea erabiltzea.
Aplikatu Kirchhoff-en tentsio legea (KVL) sare bakoitzaren inguruan, sare korronteen norabide berean. Erresistentziak haren bidez bi sare korronte edo gehiago baditu, erresistentziaren bidez korronte osoa sare korronteen batura aljebraikoa da. Beste modu batera esanda, erresistentziatik igarotzen den korronteak begiztaren sare korrontearen norabide berdina baldin badu, zeinu positiboa du, bestela batuketan seinale negatiboa. Tentsio iturriak ohi bezala kontutan hartzen dira. Beren norabidea sare korrontearen berdina bada, haien tentsioa positibotzat hartzen da, bestela negatiboa, KVLren ekuazioetan. Normalean, korronte iturriei dagokienez, sare korronte bakarra iturtzen da iturrian, eta korronteak iturriaren korrontearen norabide bera du. Horrela ez bada, erabili zirkuitu korronte orokorraren metodoa, paragrafo honetan aurrerago deskribatuko dena. Ez dago KVLren ekuazioak idatzi behar iturriei esleitutako sare korronteekin.
Ebatzi ondoriozko begizta ekuazioak sare korronteak lortzeko.
Zehaztu zirkuituan eskatutako edozein korronte edo tentsio sareko korronteak erabiliz.
Erakutsi dezagun metodoa honako adibide honen bidez:
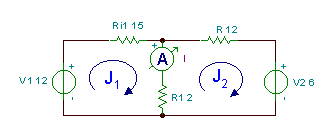
Bilatu beheko zirkuituan uneko Ia.
Zirkuitu honetan bi sare (edo ezkerreko eta eskuineko leihoa) daudela ikusten dugu. Eman diezazkiogu erloju-orratzen sareak J1 eta J2 sareetaraino. Ondoren, KVL ekuazioak idazten ditugu, erresistentzien arteko tentsioak Ohm-en legearen bidez adieraziz:
-V1 + J1* (Ri1+R1) - J2*R1 = 0
V2 - J1*R1 + J2* (R + R1) = 0
zenbakiaren:
-12 + J1* 17 - J2* 2 = 0
6 - J1* 2 + J2* 14 = 0
J adieraztea1 lehenengo ekuazioaren arabera: J1 = 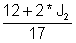

biderkatu 17: 102 - 24 + 4 * J2 + 238 * J2 = 0 horregatik J2 = 
eta J1 = 
Azkenean, beharrezkoa den unekoa:
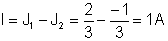
{Malla uneko metodoa}
Sys J1, J2
J1*(Ri1+R1)-J2*R1-V1=0
J1*R1+J2*(R1+R)+V2=0
bukatzen;
J1 = [666.6667m]
J2 = [- 333.3333m]
I: = J1-J2;
I = [1]
inportatu numpy n bezala
#Erabili sareko korronte metodoa!
#Ebatzi nahi dugun ekuazio-sistema lineal bat dugu
#I1,I2rako:
#I1*(Ri1+R1)+I2*Ri1-V1=0
#-V1+I1*Ri1+I2*(Ri1+R)+V2=0
#Idatzi koefizienteen matrizea:
A=n.array([[Ri1+R1,Ri1],[Ri1,Ri1+R]])
#Idatzi konstanteen matrizea:
b=n.array([V1,V1-V2])
x=n.linalg.solve(A,b)
I1=x[0]
I2=x[1]
inprimatu ("I1= %.3f"%I1)
inprimatu ("I2= %.3f"%I2)
I=I1
inprimatu ("I= %.3f"%I)
Emaitzak egiaztatu TINArekin:
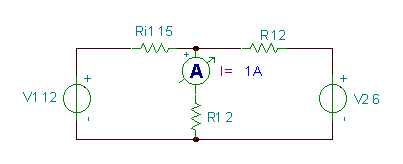

Ondoren, konpondu dezagun aurreko adibidea berriro, baina orokorragoekin begizta korronteen metodoa. Metodo hau erabiliz, itxita dauden uneko begiztak deitzen dira begizta korronteak, ez dira nahitaez zirkuituaren sareetara lotzen, arbitrarioa baizik begizta independenteak. Begiztapenak independenteak direla ziurtatu dezakezu, begizta batean beste osagairik ez duen gutxienez osagai bat edukiz. Zirkuitu planoetarako, begizta independenteen kopurua sareko kopuru bera da eta erraz ikusten da.
Begizta independenteen kopurua zehazteko modu zehatzagoa da.
Zirkuitu batekin b adarrak eta N nodoak. Begiztapen independenteen kopurua l da:
l = b - N + 1
Hori gertatzen da Kirchhoff-en ekuazio independenteen kopurua zirkuituaren adarren berdina izan behar dela eta jadanik badakigu bakarrik daudela N-1 nodo independentearen ekuazioak. Hortaz, Kirchhoff-en ekuazioen kopurua osoa da
b = N-1 + l eta horregatik l = b - N + 1
Ekuazio hau gune honetan gerora deskribatuko den grafiaren teoriaren funtsezko teorematik dator.
Orain konpondu dezagun aurreko adibidea berriro, baina besterik gabe, begizta korrontearen metodoa erabiliz. Metodo honen bidez libre gaude begiztak sareetan edo beste edozein begiztetan erabiltzeko, baina jarrai dezagun begiz J-rekin1 zirkuituaren ezkerreko sarean. Hala ere, bigarren begiztarako J begia aukeratzen dugu2, beheko irudian ikusten den bezala. Aukera honen abantaila J da1 eskatutako korrontearen I berdina izango da, R1etik pasatzen den begizta korronte bakarra baita. Horrek esan nahi du ez dugula J2 kalkulatu behar guztietan. Kontuan izan, korronte “errealak” ez bezala, begizta korronteen esanahi fisikoa zirkuituari nola esleitzen zaion.
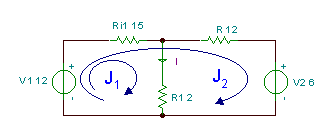

KVL ekuazioak:
J1 * (R1+Ri1) + J2 * R i1 - V.1 = 0
-V1+ J1 * Ri1+ J2 * (R + Ri) + V2 = 0
eta beharrezkoa den korrontea: I = J1
Numerically: J1*(15+2)+J2*15-12 = 0
-12 + J1 * 15 + J2 * (15 + 12) + 6 = 0
Express J2 bigarren ekuazioaren arabera:
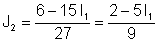
Ordeztu lehen ekuazioan:
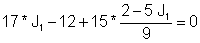
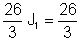
Hori dela: J1 = I = 1 A
Adibide gehiago.
Adibidea 1
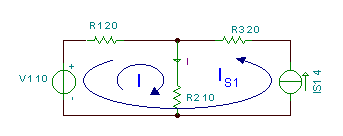
Bilatu beheko zirkuituan uneko Ia.
Zirkuitu honetan, begizta korronteen metodoa erabiltzen dugu. Zirkuituaren ezkerreko leihoan begizta korronte bat hartzen dugu I eskatutako korrontearen berdina denez. Beste begizta korrontea Is1 iturriaren korrontearen berdina da, beraz, zuzenean bezala izendatzen dugu IS1.
Kontuan izan begizta korronte honen norabidea dela ez erlojuaren kontrako erlojua korrontearen iturriak zehazten duelako. Dena den, begizta korronte hau jada ezagutzen denez, ez da zirkulaziorako KVL ekuazioa idatzi behar IS1 hartu da.
Horregatik, ebatzi beharreko ekuazio bakarra hauxe da:
-V1 + I * R2 + R1 * (I - IS1) = 0
horregatik
I = (V1 + R1 *IS1) / (R1 + R2)
zenbakiaren
I=(10+20*4)/(20+10)=3 A
Emaitza hau TINA-ren analisi sinbolikoa deituz / Analisi Sinbolikoa / DC Emaitza menutik deitu dezakezu:
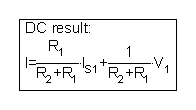
Edo interpretatu dezakezu KVLren ekuazioa:
| {TINA-ren interpretearen konponbidea} {Erabili sareko uneko metodoa} Sys I -V1 + I * R2 + R1 * (I - IS1) = 0 bukatzen; I = [3] |
Hurrengo adibideak 3 korronte iturri ditu eta oso erraz konpondu daiteke begizta korronteen metodoaren arabera.
Adibidea 2
Bilatu V. tentsioa
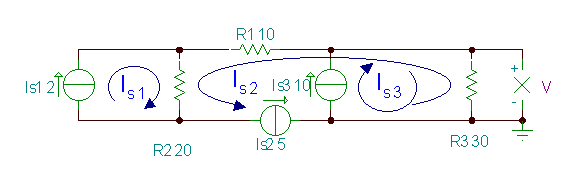

Adibide honetan, hiru begizta korronte aukera ditzakegu, bakoitza korronte iturri bakarra igarotzeko. Beraz, hiru begiztako korronte guztiak ezagutzen dira, eta tentsio ezezaguna, V, adierazi behar dugu, horiek erabiliz.
Korronteen batuketa algebraikoa R bidez egitea3:
V = (IS3 - NiS2) * R3= (10-5) * 30 = 150 V. TINA honekin egiaztatu dezakezu:.
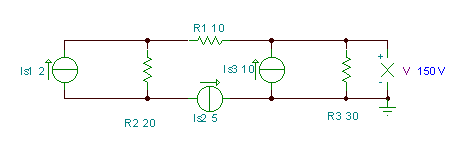

Ondoren, berriro konpondu dugun arazoari aurre egin diezaiokegu Kirchhoffen legeak Nodoaren metodo potentziala kapituluak.
Adibidea 3
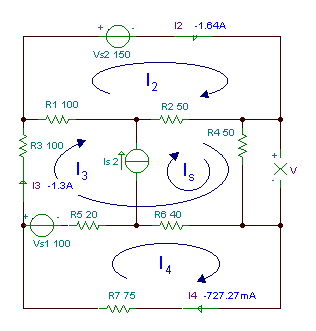
Bilatu R erresistentziaren V tentsioa4.
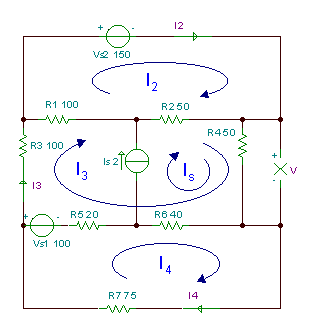

R1 = R3 = 100 ohm, R2 = R4 = 50 ohm, R5 = 20 ohm, R6 = 40 ohm, R7 = 75 ohm.
Arazo honek aurreko kapituluetan gutxienez 4 ekuazio behar zituen konpontzeko.
Arazo hau begizta korronteen metodoarekin konponduz, lau begizta independente ditugu, baina begizta korronteen aukera egokiarekin, begizta korronteetako bat iturburu korrontearen berdina izango da.
Goiko irudian agertzen diren begizta korronteak oinarritzat hartuta, begiztaren ekuazioak hauek dira:
VS1+I4* (R5+R6+R7) - IS*R6 -I3* (R5 + R6) = 0
VS2 - Ni3* (R1+R2) - IS*R2 + I2* (R1 + R2) = 0
-VS1 + I3* (R1 + R2 + R3 + R4 + R5 + R6) +S* (R2 +R4 + R6) - I4* (R5 + R6) - Ni2* (R1 + R2) = 0
Tentsio ezezaguna V begizta korronteen bidez adieraz daiteke:
V = R4 * (I2 + I3)
zenbakiaren:
100 + I4* 135-2 * 40-I3* 60 = 0
150 + I2* 150-2 * 50-I3* 150 = 0
-100 + I3* 360 + 2 * 140-I4* 60-I2* 150 = 0
V = 50 * (2 + I3)
Cramerren araua erabil dezakegu ekuazioen sistema hau konpontzeko:
I4 = D3/D
non D sistemaren determinatzailea da. D4, I.aren determinatzailea4, Sistemaren eskuinaldean I zutabearen ordez kokatzen da4koefizienteak.
Ordenatutako ekuazioen sistema:
- 60 * I3 + 135 * I4= -20
150 * I2-150 * I3 = - 50
-150 * I2+ 360 * I3 - 60 * I4= - 180
Beraz, determinantea D:
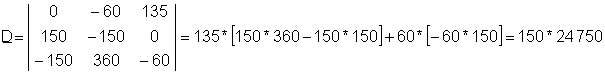
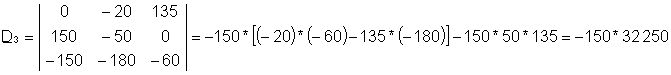
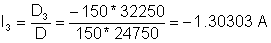
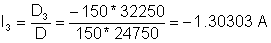
Ekuazio sistema honen konponbidea honakoa da:
V = R4* (2 + I3) = X V
Erantzuna TINAk kalkulatutako emaitzaren bidez berretsi dezakezu.
Sys I2, I3, I4
Vs2+I2*(R1+R2)-R2*Is-I3*(R1+R2)=0
-Vs1+I3*(R1+R2+R3+R4+R5+R6)+Is*(R2+R4+R6)-I2*(R1+R2)-I4*(R5+R6)=0
Vs1+I4*(R5+R6+R7)-Is*R6-I3*(R5+R6)=0
bukatzen;
I2 = [- 1.6364]
I3 = [- 1.303]
I4 = [- 727.2727m]
V: = R4 * (+ da I3);
V = [34.8485]
inportatu numpy n bezala
#Ebatzi nahi dugun ekuazio-sistema lineal bat dugu
# I1, I2, I3, I4rako:
#I1=Da
#Vs2+I2*(R1+R2)-R2*I1-I3*(R1+R2)=0
#-Vs1+I3*(R1+R2+R3+R4+R5+R6)+I1*(R2+R4+R6)-I2*(R1+R2)-I4*(R5+R6)=0
#Vs1+I4*(R5+R6+R7)-I1*R6-I3*(R5+R6)=0
#Idatzi koefizienteen matrizea:
A=n.array([[1,0,0,0],[-R2,R1+R2,-(R1+R2),0],[R2+R4+R6,-(R1+R2),R1+R2+R3+R4+R5+R6,-(R5+R6)],[-R6,0,-(R5+R6),R5+R6+R7]])
#Idatzi konstanteen matrizea:
b=n.array([Is,-Vs2,Vs1,-Vs1])
x=n.linalg.solve(A,b)
I1,I2,I3,I4=x[0],x[1],x[2],x[3]
print(“I1= %.5f”%I1) #x[0]=I1
print(“I2= %.5f”%I2) #x[1]=I2
print(“I3= %.5f”%I3) #x[2]=I1
print(“I4= %.5f”%I4) #x[3]=I2
V=R4*(I1+I3)
inprimatu ("V= %.5f"%V)
Adibide honetan, begizta korronte ezezagun bakoitza adar korronte bat da (I1, I3 eta I4); beraz, erraza da emaitza TINAren analisi DCko emaitzekin konparatzea.