Egin klik beheko edo Idatzi beheko zirkuituak TINACloud deitzeko eta hautatu Lineako DC interaktiboa hautatzeko.
Egin klik beheko edo Idatzi beheko zirkuituak TINACloud deitzeko eta hautatu Lineako DC interaktiboa hautatzeko. Eskuratu TINACloud-era kostu txikia adibide horiek editatzeko edo zure zirkuituak sortzeko
Ekuazioaren bidez deskribatu daiteke tentsio sinusoidal bat:
v (t) = VM sin (ωt + Φ) edo v (t) = VM cos (ωt + Φ)
| non | v (t) | Tentsioaren berehalako balioa, voltetan (V). |
| VM | Tentsioaren gehienezko edo gehienezko balioa, volt (V) | |
| T | Garaia: ziklo bateko denbora, segundotan | |
| f | Maiztasuna - 1en bigarren denboren kopurua, Hz (Hertz) edo 1 / s. f = 1 / T | |
| ω | Angular frekuentzia, radianez / s adierazita ω = 2 * π * f edo ω = 2 * π / T. | |
| Φ | Hasierako fasea radianetan edo graduetan emana. Zenbatekoa sinusiaren edo kosinuaren uhinaren balioa = 0 balioa zehazten du. | |
| Oharra: Tentsio sinusoidal baten anplitudea V batzuetan adierazten daEFF, eraginkorra edo RMS balioa. Hau da V lotutaM harremanaren araberaM= √2VEFF, edo gutxi gorabehera VEFF = X VM |
Hona hemen aipatutako terminoak ilustratzeko adibide batzuk.
Europako 220 V AC tentsioaren propietateak.
Balio eraginkorra: VEFF = X V
Gorako balioa: VM= √2 * 220 V = 311 V
Maiztasuna: f = 50 1 / s = 50 Hz
Angular frekuentzia: ω = 2 * π * f = 314 1 / s = 314 rad / s
Epea: T = 1 / f = 20 ms
Denbora funtzioa: v (t) = 311 sin (314 t)
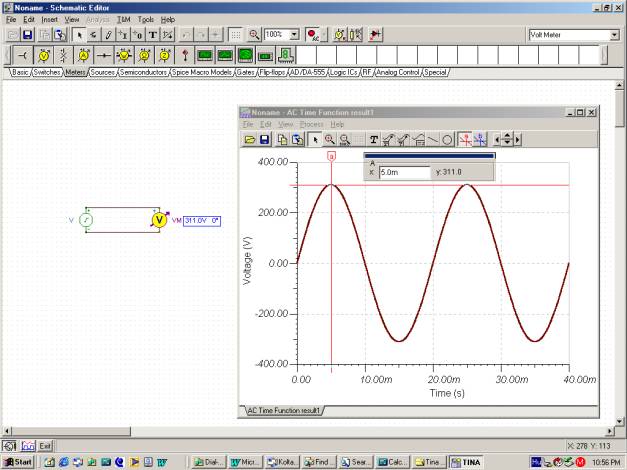
Ikus dezagun denbora-funtzioa TINA-ren Analisi / AC analisia / Denbora funtzioaren komandoa erabiliz.
Aldia T = 20m eta V dela egiaztatu dezakezuM = X V.
AEBetako 120 V AC tentsioaren propietateak.
Balio eraginkorra: VEFF = X V
Gorako balioa: VM= 2 120 V = 169.68 V ≈ 170 V
Maiztasuna: f = 60 1 / s = 60 Hz
Angular frekuentzia: ω = 2 * π * f = 376.8 rad / s ≈ 377 rad / s
Epea: T = 1 / f = 16.7 ms
Denbora funtzioa: v (t) = 170 sin (377 t)
Kontuan izan kasu honetan denbora funtzioa eman litekeela v (t) = 311 sin (314 t + Φ) edo v (t) = 311 cos (314 t + Φ), irteerako tentsioaren kasuan ez dakit hasierako fasea.
Hasierako faseak garrantzi handia du aldi berean hainbat tentsio aurkezten direnean. Adibide praktiko on bat hiru faseko sistema da, non hiru puntuko balio, forma eta frekuentzia bereko tentsioetan dauden, eta horietako bakoitzak 120 ° fasea gainontzekoekin alderatzen du. 60 Hz sare batean, ordua funtzioak dira:
vA(t) = 170 sin (377 t)
vB(t) = 170 sin (377 t - 120 °)
vC(t) = 170 sin (377 t + 120 °)
TINA-rekin egindako hurrengo irudiak denbora horiekin funtzionatzen duen zirkuituak erakusten ditu TINA-ren tentsioko sortzaile gisa.
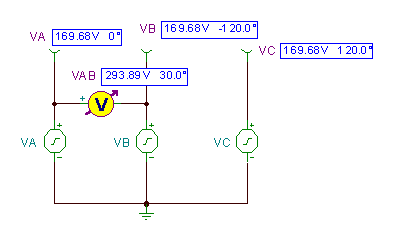

Tentsio aldea vAB= vA(t) - vB(t) TINA-ren Analisi / AC analisia / Denbora funtzioaren komandoaren bidez konpondu da.
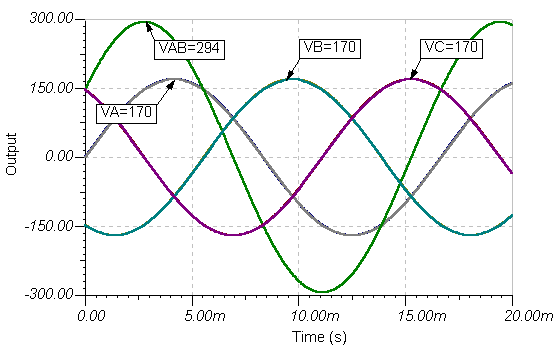

Kontuan izan vAB (t) gutxi gorabehera 294 V da, v X-en V X baino handiagoaA(t) edo vB(t) tentsioak, baina ez soilik beren goi tentsioen batura. Hau da fase aldea dela eta. Ondorioz sortutako tentsioa nola kalkulatuko dugu (hau da ,. Ö3 * 170 @ 294 kasu honetan, geroago, kapitulu honetan eta bestea ere bereizita Hiru Faseko Sistemak kapitulu.
Seinale sinusoidalen balioak
Hala ere, AC-ren seinalea aldian aldatzen den bitartean, erraza da zenbait uhin bereiztea olatu bat beste batekin konparatzeko: Hauek dira gailuak, batez bestekoak eta erro-bitartekoak (rms).
Gehieneko balioa betetzen dugu VM hau da, denboraren funtzioaren gehienezko balioa, olatu sinusoidalaren anplitudea.
Batzuetan, gailur-gailurra (pp) balioa erabiltzen da. Tentsio eta korronte sinusoidalei dagokienez, gailurra eta gailurra duen balioa gailen balio bikoitza da.
The batez besteko balioa sine-uhinaren erdiko ziklo positiboaren balio aritmetikoen batez bestekoa da. Ere deitzen zaio batez besteko absolutua uhinaren balio absolutuaren batez bestekoaren berdina baita. Praktikan, uhin hau aurkitzen dugu errektifikazioa uhin sinusoiduna uhin zuzentzailea izeneko zirkuitu batekin.
Olatu sinusoidal baten batez besteko absolutua honakoa da:
VAV= 2 / π VM 0.637 VM
Kontuan izan ziklo osoen batez bestekoa zero dela.
Tentsio edo korronte sinusoidale baten balio efektibo edo efektukoak baliozko DC balio baliokide bat suposatzen du berokuntza potentzia bera sortzen duena. Adibidez, 120 V-ren balio eraginkorra duen tentsio bat berogailu eta argiztapen berdinaren potentzia bera sortzen da bonbilla batean 120 V, DC tentsioko iturri batetik. Olatu sinusoidal baten balio erreala edo eraginkorra dela frogatu daiteke:

Vrms = VM / √2 ≅ 0.707 VM
Balio hauek modu berean kalkulatu daitezke bi tentsio eta korronteetarako.
Balio erreala oso garrantzitsua da praktikan. Bestela adierazi ezean, linea elektrikoen AC tentsioak (adib. 110V edo 220V) balio errealetan ematen dira. AC metro gehienak rms kalibratuta daude eta rms maila adierazten dute.
Adibidea 1 Bilatu sare elektrikoaren tentsio sinusoidalaren gailurra 220 V rms balioarekin.
VM = 220 / 0.707 = 311.17 V
Adibidea 2 Bilatu sare elektrikoaren tentsio sinusoidalaren gailurra 110 V rms balioarekin.
VM = 110 / 0.707 = 155.58 V
Adibidea 3 Aurki tentsio sinusoidearen (absolutua) batez bestekoa, bere balio errematikoa bada 220 V.
Va = 0.637 * VM = 0.637 * 311.17 = 198.26 V
Adibidea 4 Aurki tentsio sinusoidalaren batez besteko absolutua, bere rms balioa 110 V.
2 adibideko tentsioaren gailurra X eta ondorioz:
Va = 0.637 * VM = 0.637 * 155.58 = 99.13 V
Adibidea 5 Bilatu batez besteko absolutuaren arteko erlazioa (V.)a) eta uhin (V) balioak sinusoidalearen uhinaren balioetarako.
V / Va = 0.707 / 0.637 = 1.11
Kontuan izan ezin duzula AC zirkuituan batez besteko balioak gehitu, emaitzak desegokiak eramaten baititu.
fasoreak
Aurreko atalean ikusi dugun moduan, askotan beharrezkoa da AC zirkuituetan maiztasun bereko tentsio eta korronte sinusoidalak gehitzea. Nahiz eta seinaleak TINA erabiliz zenbakiak gehitzea edo harreman trigonometrikoak erabiliz, komenigarria da deiturikoak erabiltzea. fasore metodoa. Faseor batek seinale sinusoidal baten anplitudea eta fasea adierazten duen zenbaki konplexua da. Garrantzitsua da fasorrak ez du fazore guztientzat berdinak izan behar.
Fasore batek zenbaki konplexu gisa kudeatu daiteke edo grafikoki irudikatzen da plano konplexuan gezi lau gisa. Irudikapen grafikoa fasor diagrama deitzen zaio. Fasoreko diagramak erabiliz, fasors planoak konplexu batean gehitu edo ken ditzakezu triangeluaren edo paralelogramoaren arauaren arabera.
Zenbaki konplexuen bi forma daude: angeluzuzenak polar.
Laukizuzenaren irudikapena forma + da jb, non j = Ö-1 irudizko unitatea da.
Polar ordezkaritza Ae forman dagoj j , non A balio absolutua (anplitudea) eta f Faseor angeluaren angelu errealeko ardatz positibotik, ezkerretara.
Erabiliko dugu kantitate konplexuen letrak.
Ikus dezagun denbora-funtzio batetik dagokion fasorea nola lortzen den.
Lehenik eta behin, suposatu zirkuituko tentsio guztiak kosinu-funtzioen bitartez adierazten direla. (Tentsio guztiak forma horretara bihur daitezke.) Ondoren fasore v (t) = V tentsioari dagokionezM cos ( w t+f) da: VM = VMe jf , hau da, baita ere, puntu konplexuena.
Adibidez, kontuan hartu tentsioa: v (t) = 10 cos ( w t + 30°)
Dagokion fasor: 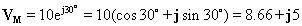
Denboraren funtzioa fasoretik ere kalkulatu ahal izango dugu. Lehenengo fasea polar moduan idazten dugu adibidez VM = VMe jr eta orduan dagokion denbora funtzioa da
v (t) = VM (Cos (wt+r).
Adibidez, kontuan hartu fasorea VM = 10 - j20 V
Inprimaki polarrari ekartzea:
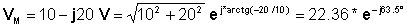
Horregatik, denbora funtzio hau da: v (t) = 22.36 cos (wt - 63.5°) V
Phasoreak AC zirkuituetako tentsio eta korronteen eraginkortasun konplexua edo rms balioa zehazteko maiz erabiltzen dira. Emandako v (t) = VMcos (wt+r) = 10cos (wt + 30°)
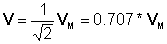
zenbakiaren:
v (t) = 10 * cos (wt-30°)
Eraginkorra (rms) balioa konplexua: V = 0.707 * 10 * e- j30° = EZ e- j30° = 6.13 - j 3.535
Alderantziz: tentsio baten balio eraginkor konplexua bada:
V = - 10 + j 20 = 22.36 e j 116.5°
ondoren konplexua gailurra balioa: 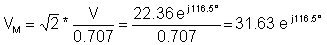
eta denbora funtzioa: v (t) = 31.63 cos ( wt + 116.5° ) V
Aurreko tekniken justifikazio laburra honako hau da: Denbora funtzio bat eman
VM (Cos ( w t+r), definitu dezagun konplexua denboraren funtzioa gisa:
v (t) = VM e jr e jwt = VMe jwt = VM (Cos (r) + j sin (r)) E jwt
non VM =VM e j r t = VM (Cos (r) + j sin (r)) ezarritako fasor bakarra da.
Adibidez, v (t) = 10 cos-eko denbora funtzioakwt + 30°)
v (t) = VMe jwt = EZ e j30 e jwt = 10e jwt (cos (30) + j sin (30)) = e jwt (8.66 +j5)
Denbora funtzio konplexua sartuz, benetako parte bat eta irudimenezko zati bat irudikatzen dugu. Denboraren jatorrizko benetako funtzioa beti berreskura dezakegu gure emaitza erreala hartzen duena: v (t) = Re {v(T)}
Hala ere, denboraren funtzio konplexuak abantaila handia du, kontuan hartzen diren AC zirkuituan denboraren funtzio konplexu guztiak ejwt biderkatzailea, hau faktore dezakegu eta besterik gabe funtoreekin lan egin dezakegu. Gainera, praktikan ez dugu ejwt zati bat, besterik gabe, denbora funtzioetatik fasoreetara eta atzera egindako transformazioak.
Fasoreen erabileraren abantaila erakusteko, ikusi hurrengo adibidea.
Adibidea 6 Bilatu batura eta tentsioen aldea:
v1 = 100 cos (314 * t) v2 = 50 cos (314 * t-45.)°)
Lehenengo bi tentsioen fasoreak idatzi:
V1M = 100 V2M= EZ e - j 45° = 35.53 - j 35.35
Hori dela:
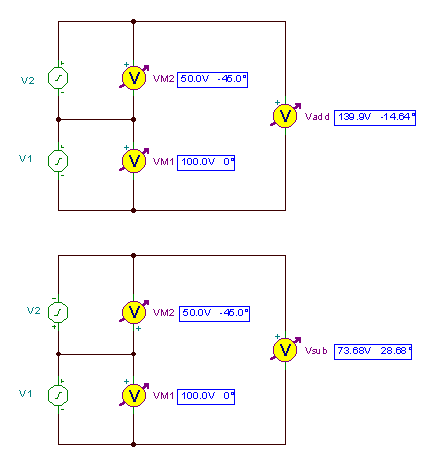
Vgehitu = V1M + V2M = 135.35 - j 35.35 = 139.89 e- j 14.63°
Vazpi = V1M - V2M = 64.65 + j35.35 = 73.68 e j 28.67°
eta gero denbora funtzioak:
vgehitu(t) = 139.89 * coswt - 14.63°)
vazpi(t) = 73.68 * coswt + 28.67°)
Adibide sinple honek erakusten duen moduan, phasors metodoa AC arazoa konpontzeko tresna indartsua da.
Arazoa konpondu dezagun TINA interpretearen tresnak erabiliz.
{v1 + v2-aren kalkulua}
v1: = 100
v2: = 50 * exp (-PI / 4 * j)
v2 = [35.3553-35.3553 * j]
v1add: = v1 + v2
v1add = [135.3553-35.3553 * j]
abs (v1add) = [139.8966]
radtodeg (arku (v1add)) = [- 14.6388]
{v1-v2-aren kalkulua}
v1sub: = v1-v2
v1sub = [64.6447 + 35.3553 * j]
abs (v1sub) = [73.6813]
radtodeg (arku (v1sub)) = [28.6751]
#v1+v2-ren kalkulua
inportatu matematika m gisa
inportatu cmath gisa c
v1=100
v2=50*c.exp(konplexua (0,-c.pi/4))
inprimatu ("v2=",v2)
vadd=v1+v2
inprimatu ("vadd=", vadd)
inprimatu ("abs(vadd)=",abs(vadd))
inprimatu("graduak(arkua(vadd))=",m.graduak(c.fasea(vadd)))
#v1-v2-ren kalkulua
vsub=v1-v2
inprimatu ("vsub=",vsub)
inprimatu ("abs(vsub)=",abs(vsub))
inprimatu ("graduak(arkua(vsub))=",m.graduak(c.fasea(vsub)))
Handiaren eta anplitudearen emaitzak eskuko kalkuluak baieztatzen dituzte.
Orain, TINA-ren AC azterketaren emaitza egiaztatuko dugu.
Azterketa egin aurretik, ziurtatu AC funtzioa ia ezarri kosinu in the Editorearen aukerak Ikusi / Aukeren menuko elkarrizketa-koadroa. Parametro honen eginkizuna azalduko dugu Adibidea 8.
Zirkuituak eta emaitzak:
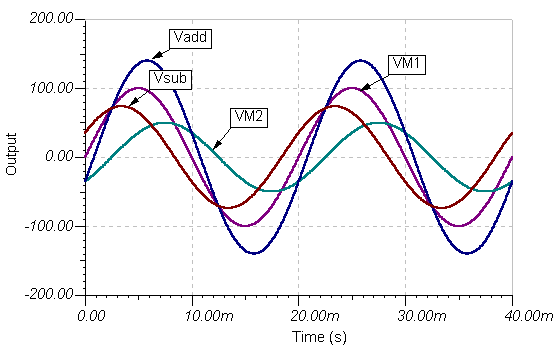
Berriro ere emaitza berdina da. Hona hemen denbora funtzioaren grafikoak:
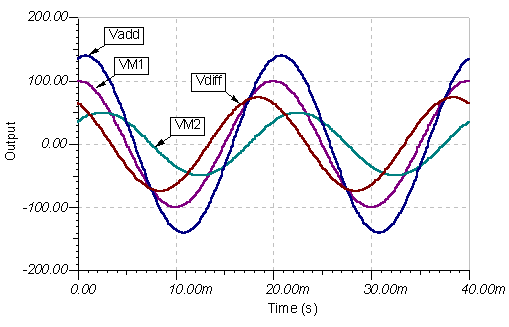
Adibidea 7 Bilatu batura eta tentsioen aldea:
v1 = 100 sin (314 * t) eta v2 = 50 cos (314 * t-45.)°)
Adibide honek galdera berri bat sortzen du. Orain arte, denbora funtzio guztiak kosinu funtzioak eman behar ditugu. Zer egin behar dugu denbora sinu gisa emandako denbora-funtzioarekin? Irtenbidea sine funtzioa kosinu funtzioa bihurtzea da. Sin (x) = cos trigonometriko erlazioaren bidez (x-)p/ 2) = cos (x-90°), gure adibidea honela itzul daiteke:
v1 = 100 cos (314t - 90°) v2 = 50 cos (314 * t - 45°)
Orain tentsioen fasorrak hauek dira:
V1M = EZ e - j 90° = -100 j V2M= EZ e - j 45° = 35.53 - j 35.35
Hori dela:
V gehitu = V1M + V2M = 35.53 - j 135.35
V azpi = V1M - V2M = - 35.53 - j 64.47
eta gero denbora funtzioak:
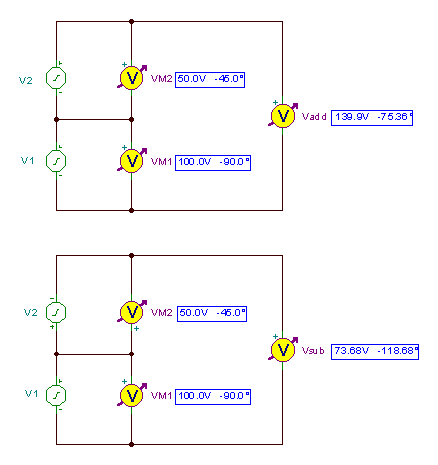
vgehitu(t) = 139.8966 cos (wt-75.36°)
vazpi(t) = 73.68 cos (wt-118.68°)
Arazoa konpondu dezagun TINA interpretearen tresnak erabiliz.
{v1 + v2-aren kalkulua}
v1: = - 100 * j
v2: = 50 * exp (-PI / 4 * j)
v2 = [35.3553 - 35.3553 * j]
v1add: = v1 + v2
v1add = [35.3553-135.3553 * j]
abs (v1add) = [139.8966]
radtodeg (arku (v1add)) = [- 75.3612]
{v1-v2-aren kalkulua}
v1sub: = v1-v2
v1sub = [- 35.3553 - 64.6447 * j]
abs (v1sub) = [73.6813]
radtodeg (arku (v1sub)) = [- 118.6751]
#v1+v2-ren kalkulua
inportatu matematika m gisa
inportatu cmath gisa c
v1=100
v2=50*c.exp(konplexua (0,-c.pi/4))
inprimatu ("v2=",v2)
vadd=v1+v2
inprimatu ("vadd=", vadd)
inprimatu ("abs(vadd)=",abs(vadd))
inprimatu("graduak(arkua(vadd))=",m.graduak(c.fasea(vadd)))
#v1-v2-ren kalkulua
vsub=v1-v2
inprimatu ("vsub=",vsub)
inprimatu ("abs(vsub)=",abs(vsub))
inprimatu ("graduak(arkua(vsub))=",m.graduak(c.fasea(vsub)))
Ikus dezagun TINA en AC analisiarekin
Adibidea 8
Bilatu batura eta tentsioen aldea:v1 = 100 sin (314 * t) v2 = 50 sin (314 * t-45°)
Adibide honek beste gai bat sortzen du. Zer gertatzen da tentsio guztiak olatu sinusoiko gisa emango bagenu eta emaitzak uhin gisa ikusi nahi ditugu?. Bi tentsioak kosinu funtzio bihur ditzakegu, erantzuna kalkulatu eta emaitza berriro sinus funtzio bihur dezakegu, baina ez da beharrezkoa. Sinus uhinetatik fasoreak sor ditzakegu kosinu uhinetatik egin genuen modu berean eta, ondoren, haien anplitudea eta faseak sinus uhinen anplitudea eta fasea bezala erabil ditzakegu emaitzan.
Hau da, noski, olatu sinusoidala olatu kosinuetara eraldatzearen ondorioz. Aurreko adibidean ikusi genuen bezala, hau biderkagarria da -j eta gero cos (x) = sin erabiliz (x-90.)°) erlazio sinusoide bihurtzeko. Hau biderkatzea baliokidea da j. Beste era batera esanda, geroztik -j × j = 1, olatu sinusoien anplitudeak eta faseak zuzenean eratorritako fasorrak erabil ditzakegu funtzioa irudikatzeko eta, ondoren, zuzenean itzultzeko. Era berean, denbora funtzio konplexuei buruz modu berean arrazoituz, olatu sinusuenak denbora konplexuaren funtzio konplexuen zatiak kontuan hartu ahal izango ditugu eta horien osaera kosinuarekin osatuko dute, denbora konplexu osoa funtzioa sortzeko.
Ikus dezagun adibide honen konponbidea sinus funtzioak fasoreen oinarri gisa erabiliz (sin transformatzailea ( w t) benetako unitate fasororako (1)).
V1M = 100 V2M= EZ e - j 45° = 35.53 - j 35.35
Hori dela:
V gehitu = V1M + V2M = 135.53 - j 35.35
V azpi = V1M - V2M = 64.47+ j 35.35
Kontuan izan fasorrak 6 adibidean zeudela eta ez denbora funtzioak berdinak direla:
v3(t) = 139.9sin (wt - 14.64°)
v4(t) = 73.68sin (wt 28.68 +°)
Ikus dezakezun moduan, oso erraza da emaitza lortzea sen funtzioak erabiliz, batez ere gure hasierako datuak sinu uhinak direnean. Testuliburu askok nahiago dute uhin sinusitarioa fazoreen oinarrizko funtzio gisa erabiltzea. Praktikan, edozein metodo erabil dezakezu, baina ez nahastu.
Fasoroak sortzean, oso garrantzitsua da denbora funtzio guztiak lehenbizi sinu edo kosinu bihurtzen direla. Funtzio siniketatik abiatzen bazara, zure soluzioak funtzio sinbolikoak irudikatu beharko lirateke, funtoreetatik denbora funtzioetara itzultzean. Gauza bera gertatzen da funtzio kosinuarekin hasten baduzu.
Arazo bera konpondu dezagun TINA modu interaktiboan. Sinusiak funtzioak sortzeko oinarri gisa erabili nahi dugunez, ziurtatu AC funtzioa ezarri da sine in the Editorearen aukerak Ikusi / Aukeren menuko elkarrizketa-koadroa.
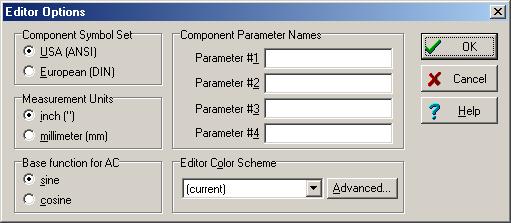

Olatuen batuketa eta desberdintasuna egiteko zirkuituak:
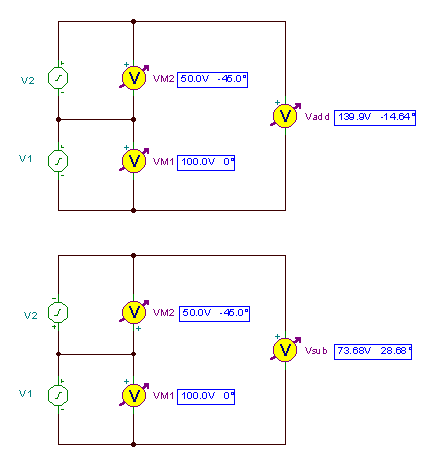
eta denboraren funtzioak: