 TINACloud बोल्नका लागि तलको उदाहरण सर्किटहरूमा ट्याप गर्नुहोस् वा ट्याप गर्नुहोस् र तिनीहरूलाई अनलाईन विश्लेषण गर्न अन्तरक्रियात्मक डीसी मोड चयन गर्नुहोस्।
TINACloud बोल्नका लागि तलको उदाहरण सर्किटहरूमा ट्याप गर्नुहोस् वा ट्याप गर्नुहोस् र तिनीहरूलाई अनलाईन विश्लेषण गर्न अन्तरक्रियात्मक डीसी मोड चयन गर्नुहोस्। उदाहरणहरू सम्पादन गर्न वा आफ्नै सर्किटहरू सिर्जना गर्न TINACloud लाई कम लागत पहुँच पाउनुहोस्
यो र निम्न अध्यायमा, हामी एक धेरै महत्त्वपूर्ण विषय प्रस्तुत गर्नेछौं: एसी, वा वैकल्पिक चलिरहेको। हालको वैकल्पिक नाम अत्यन्तै सटीक छैन र सामान्यतया सर्कुइट्सहरू sinusoidal voltages र धाराहरूसँग राख्छ; तथापि, वर्तमान बदल्न पनि कुनै पनि मनपर्ने वर्तमान तरंग अर्थ हो। एसी भोल्टेजको महत्त्व भनेको यो प्रकारको भोल्टेज मुख्य संसारको घर र उद्योगमा मुख्य विद्युत स्रोतको लागि प्रयोग गरिन्छ। यो धेरै इलेक्ट्रनिक्स, दूरसंचार र औद्योगिक अनुप्रयोगहरूको आधार हो।
Sinusoidal waveforms र तिनीहरूसँग सम्बन्धित सर्किटहरू संभाल्न, हामी फर्महरूको विधि भनिन्छ सरल र सुरुचिपूर्ण विधि प्रयोग गर्नेछौं। फोर्स जटिल जटिल संख्याहरु को गुणमा आधारित छ, जुन sinusoidal मात्रा को प्रतिनिधित्व को लागि आदर्श हो। यस अध्यायमा, हामी जटिल संख्या र उनीहरूको अपरेशनको बारेमा मुख्य तथ्यहरू संक्षेप गर्नेछौं। हामी पनि टिनाको अनुवादक जटिल जटिल संख्या संग गणना गर्न कसरी सजिलो बनाउनेछौं।
जटिल संख्याहरू दुई भाग, ए वास्तविक भाग (x), जुन वास्तविक अंक हो, र एउटा भनिन्छ काल्पनिक भाग (y), जुन वास्तविक नम्बर होईन 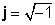
z = x + jy
जहाँ 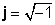
जटिल संख्याका उदाहरणहरू:
z 1 = 1 + j
z 2 = 4-2 j
z 3 = 3- 5j
जटिल संख्याहरू मूल रूपमा सत्रौं शताब्दीमा बहुपदहरू जरा प्रतिनिधित्व गर्न शुरू गरिएको थियो जुन वास्तविक संख्याको साथ मात्र प्रतिनिधित्व हुन सक्दैन। उदाहरण को लागी समीकरण x को जरा2 + 2x + 2 = 0 केवल रूपमा वर्णन गर्न सकिन्छ 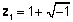
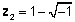
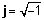
जटिल सङ्ख्याको ज्यामितीय प्रतिनिधित्व
आयताकार रूप
किनभने एक जटिल संख्या सँधै यसको वास्तविक र जटिल भागहरूमा विभाजन गर्न सकिन्छ, हामी एक जटिल संख्यालाई दुई-आयामिक विमानमा पोइन्टको रूपमा प्रतिनिधित्व गर्न सक्छौं। जटिल संख्याको वास्तविक भाग भनेको वास्तविक अक्षमा पोइन्टनको प्रक्षेपण हो, र संख्याको काल्पनिक अंश काल्पनिक अक्षमा प्रक्षेपण हो। जब एक जटिल संख्यालाई वास्तविक र काल्पनिक भागहरूको योगको रूपमा प्रस्तुत गरिन्छ, हामी भन्छौं यो भित्र छ आयताकार or विवेक रूप.
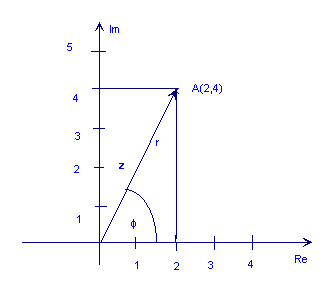
निम्न संख्याले जटिल नम्बर देखाउँछ z = 2 + 4j
ध्रुवीय र घाँटीको रूप
तपाईंले माथिको चित्रबाट देख्न सक्नुहुनेछ, पोइन्ट ए पनि एरको लम्बाईले प्रतिनिधित्व गर्न सक्दछ, r (पूर्ण मान, परिमाण, वा आयाम पनि भनिन्छ), र यसको कोण (वा चरण), φ एक काउंटरवर्क दिशा मा सापेक्ष सकारात्मक क्षैतिज अक्ष को लागी। यो छ ध्रुवीय एक जटिल संख्या को रूप। यसलाई r as को रूपमा दर्साउँछ φ.
अर्को चरण धेरै महत्त्वपूर्ण छ। ध्रुवीय रूपमा एक जटिल संख्या पनि लेख्न सकिन्छ घातक फारम:
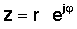
यो सरल अभिव्यक्ति विशिष्ट छ किनकि यसमा काल्पनिक संख्या हुन्छ वास्तविक वास्तविक संख्याको सट्टा। यो जटिल घाता .्ग एक वास्तविक तर्कको साथ घातीय कार्य भन्दा धेरै भिन्न व्यवहार गर्दछ। जबकि ईx x> ० बढाउनको लागि परिमाणमा द्रुत रूपमा बढ्छ र x <०, प्रकार्यका लागि घट्छ 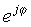
Euler को सूत्र जटिल संख्याहरु को आयताकार, ध्रुवीय, र घातीय रूपहरु को बीच एकजुट लिंक प्रदान गर्दछ:
z = x + jy = re jφ = r (cos φ + j पाप φ )
जहाँ 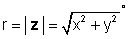
र φ = तान्न-1 (y / x)।
माथिको उदाहरणको लागि, z = 2 + 4j:
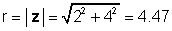
φ = तान्न-1 (4 / 2) = 63.4 °
यसैले 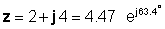
वा उपाध्यक्ष:
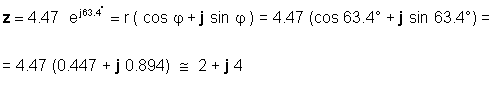
तपाइँ दुबै फारमहरू प्रयोगमा निपुण हुनुपर्दछ, अनुप्रयोगमा निर्भर रहँदै। उदाहरण को लागी, संख्याहरु आयताकार रूप मा छन् जब जोड वा घटाउ स्पष्ट रूपमा गर्न सजिलो छ, जबकि गुणन र भाग गर्न सजिलो हुन्छ जब संख्या घातांकार रूप मा हुन्छन्।
जटिल नम्बरहरूसँग सञ्चालन
अपरेसन जुन कि जटिल संख्याहरूको साथ गर्न सकिन्छ वास्तविक संख्याका लागि ती समान हुन्। नियम र केहि नयाँ परिभाषा तल सारिएका छन्।
जे साथ संचालन
यसका साथ सञ्चालन j केवल कल्पनात्मक इकाईको परिभाषाबाट पछ्याउनुहोस्,


छिटो र सही काम गर्न सक्षम हुन, तपाइँ यी नियमहरू याद गर्नुपर्छ:
j 2 = -1
j 3 =-j
j 4 =1
1/j = -j
j2 = -1 सरल को परिभाषा बाट पछ्याउँछ 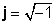
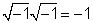
1 को लागी /j, हामी 1 /jby j / j = 1 र प्राप्त गर्नुहोस् j/ (जे जे) = j / (- १) = -j.
परिसर कन्जुगेट
एक जटिल संख्या को जटिल conjugate सजिलै संग व्युत्पन्न छ र धेरै महत्वपूर्ण छ। आयताकार रूपमा जटिल संख्याको जटिल जटिल संजाल प्राप्त गर्न, केवल कल्पनात्मक चिन्हको चिन्ह परिवर्तन गर्नुहोस्। घातक फारममा एक नम्बरको लागि त्यसो गर्न, यसको पूर्ण मान राख्दा कम्तिमा सङ्ख्याको कोणको परिवर्तन परिवर्तन गर्नुहोस्।
एक जटिल संख्या को जटिल conjugate z प्राय: द्वारा अनुमोदन गरिन्छ z*.
जटिल नम्बर दिईयो z= a + jबी, यसको जटिल कन्जगेट हो z*= a- jb.
If z घातीय रूप मा दिइएको छ, 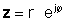
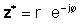
माथिको परिभाषाहरू प्रयोग गरेर, यो जटिल जटिल संख्याले जटिल जटिल संख्याले जटिल नम्बरको दायराको दायरा प्रदान गर्दछ यो हेर्न सजिलो छ:
zz* = r2 = a2 + b2
साथै, कुनै पनि जटिल संख्या र यसको संचलन थप्न वा घटाउँदा हामी निम्न सम्बन्ध पाउँछौं:
z + z * = 2a
यसैले
पुन: (z) = a = ( z + z * ) / 2
त्यसै गरी:
z - z * =j2b
यसैले
आईएम (z) = बी = ( z -z * ) / 2j
प्रमाण:
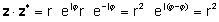
वा वास्तविक र काल्पनिक भागहरू गुणा र प्रयोग गर्दै j2= -1
zz* = (a + jब - jb) = a2+a jब jb - jbjb = a2j2 = a2 + b2
z + z* = a + jb + a - jb = 2a
z - z*= a + jb - a + jb =j2b
संख्यात्मक उदाहरणहरू:
आयताकार रूप मा:
z = 3 + j4
z* = 3- j4
zz * = 9 + 16 = 25
ध्रुवीय रूपमा
z = ∠ .5 .53.13∠.१XNUMX °
z * = ∠ 5- .53.13.१XNUMX °
घातक रूप मा:
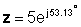
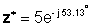
थप र घटाउ
जटिल संख्याहरूको जोड र घटाउ सीधा छ — हामीले केवल वास्तविक र काल्पनिक भागहरू अलग थप्नु पर्छ। उदाहरण को लागी, यदि
z1 = 3 - 4j र z2 = 2 + 3j
त्यसपछि
z1 + z2 = 3 - 4j + 2 + 3j = 3 + २ -।j + 3j = 5 - j
z1 - z2 = 3 - 4j - २ -j = 3 - २ -j - 3j = 1 - j7
स्पष्ट रूपमा हामीले यी अपरेसनहरूको लागि आयताकार फारम प्रयोग गर्नुपर्दछ। यदि नम्बरहरू घाता .्कन वा ध्रुवीय फारममा दिइएका छन् भने, हामीले उनीहरूलाई पहिले आयतकार फाराममा Euler को सुत्र प्रयोग गरेर रूपान्तरण गर्नुपर्नेछ, जुन पहिले दिएको छ।
गुणन
जटिल संख्याहरूको गुणनको लागि दुई विधिहरू छन्-
आयताकार रूपमा दिइएको जटिल संख्याहरूको गुणन
अपरेशन गर्न, केवल एक संख्याको वास्तविक र काल्पनिक भागहरूलाई अर्को नम्बरको वास्तविक र काल्पनिक भागहरूद्वारा गुणा गर्नुहोस् र पहिचान प्रयोग गर्नुहोस्। j2 = -1।
z1z2 = (ए1 + jb1) (a2 + jb2) = a1 a2 + jb1a2+ jb2a1 - बी1b2 = a1 a2- बी1b2 + j(b1a2+ jb2a1)
जब जटिल संख्याहरू संख्यात्मक रूपमा दिइएको छ, यो माथि सूत्र प्रयोग गर्न आवश्यक छैन। उदाहरणको लागि, गरौं
z1 = 3 - 4j र z2 = 2 + 3j
अवयवहरूको प्रत्यक्ष गुणन:
z1z2 = (3 - 4j) (2 + 3j) = 6- 8j +9j + 12 = 18 + j
वा सूत्र प्रयोग गरेर: z1z2 = a1 a2- बी1b2 + j(b1a2+ b2a1)
z1z2 = 6 + 12 + j (-8 + 9) = 18 + j
यदि तपाइँ सिधै प्रयोग गर्नुभन्दा यदि सूत्र प्रयोग गर्नुहुन्छ भने तपाईंलाई त्रुटि बनाउन अधिक सम्भव छ जस्तो लाग्छ।
Z1: = 3-4 * j
Z2: = 2 + 3 * j
Z1 * Z2 = [18 + 1 * j]
m को रूपमा गणित आयात गर्नुहोस्
c को रूपमा cmath आयात गर्नुहोस्
z1=complex('3-4j')
z2=complex('2+3j')
छाप्नुहोस्("z1*z2=", z1*z2)
ध्रुवीय वा घातक रूपमा दिइएको जटिल संख्याहरूको गुणन
यस अपरेशनको लागी, पूर्ण मानहरू गुणा गर्नुहोस् र दुई जटिल संख्याहरूको कोण जोड्नुहोस्। आउनुहोस्:
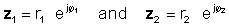
त्यसपछि घातीय कार्यको गुणको प्रयोग गरेर:
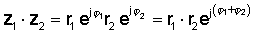
वा ध्रुवीय रूपमा
z1 z2 = r1 r2 Φ φ1 + φ2
नोट: हामीले गणना गर्दा हामीले पहिले नै यो नियम प्रयोग गर्यौं zz *माथि किनकि कन्जुगेटको कोणको मूल कोणको विपरित साइन भएको कारण, यसको आफ्नै कन्जुगेटले गुणा गरेको जटिल संख्या सँधै वास्तविक संख्या हुन्छ; अर्थात्, यसको पूर्ण मूल्यको वर्ग: zz * = r2
उदाहरणका लागि, दिनुहोस्:
z1 = ∠ ∠ °० ° र z2 = 4 ∠ -60 °
त्यसपछि
z1z2 = 20 ∠ -30 °
वा घातक रूपमा
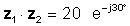
जब संख्या ध्रुवीय वा घातीय रूपमा हो भने गुणण स्पष्ट रूपमा सरल हुन्छ।
जहाँसम्म, यदि जटिल संख्याहरू आयताकार रूपमा दिइन्छ, तपाईंले सिधा गुणा कार्यहरू माथि देखाइएको अनुसार सोच्नु पर्छ, किनकि त्यहाँ अतिरिक्त चरणहरू छन् यदि तपाईंले ती संख्याहरूलाई ध्रुव रूपमा रूपान्तरण गर्नु अघि उनीहरूलाई गुणा गर्नु अघि। विचार गर्नको लागि अर्को कारक हो कि तपाईं उत्तरहरू आयताकार रूपमा वा ध्रुवीय / घातीय रूपमा हुन चाहनुहुन्छ। उदाहरण को लागी, यदि दुई अंक आयताकार रूप मा छन् तर तपाईं ध्रुवीय रूप मा आफ्नो उत्पादन चाहानुहुन्छ, यो तुरुन्तै रूपान्तरण गर्न को अर्थ छ र तिनीहरूलाई गुणा गर्नुहोस्।
विभाजन
जटिल संख्या को भाग को लागी दुई तरिकाहरु छन् -
आयताकार रूपमा दिइएको जटिल नम्बरहरूको विभाजन
अपरेशन गर्नका लागि, डिनोमिनेटरको भागको रुपमा गुणा संख्या र भाजकलाई गुणा गर्नुहोस्। डिनोमिनेटर वास्तविक संख्या हुन्छ र डिभिजन दुई जटिल संख्याको गुणामा कम हुन्छ र वास्तविक संख्याले भागलाई भाजकको निरपेक्ष मानको वर्गमान दिन्छ।
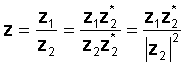
उदाहरणका लागि दिनुहोस:
z1 = 3 - 4j र z2 = 2 + 3j
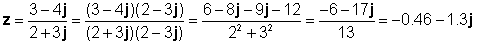
यसको परिणाम TINA को अनुवादक को साथ जाँच गरौं:
Z1: = 3-4 * j
Z2: = 2 + 3 * j
Z1 / Z2 = [- 461.5385M-1.3077 * j]
m को रूपमा गणित आयात गर्नुहोस्
c को रूपमा cmath आयात गर्नुहोस्
z1=complex('3-4j')
z2=complex('2+3j')
छाप्नुहोस्(“z1/z2=”,z1/z2)
ध्रुवीय वा घातीय फारममा दिइएको जटिल नम्बरहरूको विभाजन
अप्ठ्यारोमा लाग्न, पूर्ण मानहरू (म्याग्दीहरू) विभाजित गर्नुहोस् र अंकंकको कोणबाट डेनमार्कको कोण घटाउनुहोस्। आउनुहोस्:
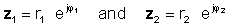
त्यसपछि घातीय कार्यहरूको विभाजनको नियम प्रयोग गरेर
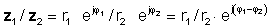
वा ध्रुवीय रूपमा
z 1 / z2 = r1 / r2 ∠ φ 1- φ 2
उदाहरणका लागि, दिनुहोस्:
z 1 = 5 ∠ 30 ° र z 2 = 2 ∠ -60 °
त्यसपछि
z 1 / z2 = ∠ .2.5 .90∠.१XNUMX °
वा घाँटी र आयताकार रूपहरूमा
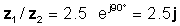
यसको परिणाम TINA को अनुवादक को साथ जाँच गरौं:
Z1: = 5 * EX (j * degtorad (30))
Z2: = 2 * एक्सपी (जे * डिग्रीटर (-60))
Z1 / Z2 = [0 + 2.5 * j]
m को रूपमा गणित आयात गर्नुहोस्
c को रूपमा cmath आयात गर्नुहोस्
z1=5*(c.exp(complex(0,m.radians(30))))
z2=2*(c.exp(complex(0,m.radians(-60))))
छाप्नुहोस्(“z1/z2=”,z1/z2)
डिभिजन स्पष्ट रूपमा सजिलो हुन्छ जब संख्या ध्रुवीय वा घाता form्कन स्वरूपमा हुन्छन्।
यद्यपि, यदि जटिल संख्याहरू आयताकार रूपमा दिइन्छ, तपाईंले जटिल कन्जुगेट विधिलाई माथि देखाईएको रूपमा सीधा डिभिजन प्रदर्शन गर्न विचार गर्नुपर्छ, किनकि त्यहाँ अतिरिक्त चरणहरू छन् यदि तपाईंले ती संख्याहरूलाई ध्रुव रूपमा रूपान्तरण गर्नु अघि उनीहरूलाई विभाजन गर्नु अघि। विचार गर्नको लागि अर्को कारक हो कि तपाईं उत्तरहरू आयताकार रूपमा वा ध्रुवीय / घातीय रूपमा हुन चाहनुहुन्छ। उदाहरण को लागी, यदि दुई अंक आयताकार रूप मा छन्, तर तपाईं ध्रुवीय रूप मा आफ्नो भागफल चाहानुहुन्छ, यो तुरुन्तै रूपान्तरण गर्न को अर्थ छ र तिनीहरूलाई विभाजन गर्नुहोस्।
अब हामी अधिक संख्यात्मक समस्याहरु द्वारा जटिल संख्याहरु को प्रयोग को वर्णन गरौं। सामान्यको रूपमा, हामी TINA को अनुवादक को प्रयोग गरेर हाम्रो समाधान जाँच गर्नेछौं। शब्दावलीले रेडिशियनसँग काम गर्दछ, तर यो रेडियनहरु को डिग्री को डिग्री या उपाध्यक्ष को रूप मा रूपांतरण को लागि मानक कार्य छ।
उदाहरण 1 ध्रुवीय प्रतिनिधित्व पत्ता लगाउनुहोस्:
z = 12 - j 48
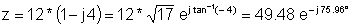
z: = 12-j * 48;
abs (z) = [49.4773]
आर्क (z) = [- 1.3258]
radtodeg (चाप (z)) = [- 75.9638]
m को रूपमा गणित आयात गर्नुहोस्
c को रूपमा cmath आयात गर्नुहोस्
z=12-जटिल(48j)
छाप्नुहोस्("abs(z)=", abs(z))
छाप्नुहोस्(“चाप(z)=”,c.phase(z))
छाप्नुहोस्("डिग्री(चाप(z))=",m.degrees(c.phase(z)))
उदाहरण 2 आयताकार प्रतिनिधित्व खोज्नुहोस्:
z = 25 ई j 125 °
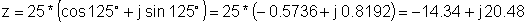
z: = 25 * एक्सपी (जे * (डर्टरडैड (125)));
z = [- 14.3394 + 20.4788 * j]
पुन: (z) = [- 14.3394]
Im (z) = [20.4788]
m को रूपमा गणित आयात गर्नुहोस्
c को रूपमा cmath आयात गर्नुहोस्
z=25*c.exp(complex(0,m.radians(125)))
छाप्नुहोस्("z=",z)
छाप्नुहोस्("वास्तविक(z)=", z.real)
छाप्नुहोस्("imag(z)=", z.imag)
उदाहरण 3 निम्न जटिल संख्याहरूको ध्रुवीय प्रतिनिधित्व पत्ता लगाउनुहोस्:
z 1 = 12 + j 48 z2 = 12 - j48 z3= -12 + j 48 z4= -12 - j 48
सबै चार नम्बरहरूको निरपेक्ष मानहरू समान छन् किनकि निरपेक्ष मान चिन्हहरूको स्वतन्त्र छ। केवल कोणहरू फरक छन्।
z1: = 12 + j * 48;
abs (z1) = [49.4773]
आर्क (z1) = [1.3258]
radtodeg (arc (z1)) = [75.9638]
Z2: = 12-j * 48;
abs (z2) = [49.4773]
आर्क (z2) = [- 1.3258]
radtodeg (चाप (z2)) = [- 75.9638]
z3: = - 12 + j * 48;
abs (z3) = [49.4773]
आर्क (z3) = [1.8158]
radtodeg (arc (z3)) = [104.0362]
Z4: = - 12-J * 48:
abs (z4) = [49.4773]
आर्क (z4) = [- 1.8158]
radtodeg (चाप (z4)) = [- 104.0362]
m को रूपमा गणित आयात गर्नुहोस्
c को रूपमा cmath आयात गर्नुहोस्
z1=complex('12+48j')
छाप्नुहोस्("abs(z1)=", abs(z1))
छाप्नुहोस्(“चाप(z1)=”,c.phase(z1))
छाप्नुहोस्(“डिग्री(चाप(z1))=”,m.degrees(c.phase(z1)))
z2=complex('12-48j')
छाप्नुहोस्("abs(z2)=", abs(z2))
छाप्नुहोस्(“चाप(z2)=”,c.phase(z2))
छाप्नुहोस्(“डिग्री(चाप(z2))=”,m.degrees(c.phase(z2)))
z3=complex('-12+48j')
छाप्नुहोस्("abs(z3)=", abs(z3))
छाप्नुहोस्(“चाप(z3)=”,c.phase(z3))
छाप्नुहोस्(“डिग्री(चाप(z3))=”,m.degrees(c.phase(z3)))
z4=complex('-12-48j')
छाप्नुहोस्("abs(z4)=", abs(z4))
छाप्नुहोस्(“चाप(z4)=”,c.phase(z4))
छाप्नुहोस्(“डिग्री(चाप(z4))=”,m.degrees(c.phase(z4)))
TINA को चाप () प्रकार्यले कुनै पनि जटिल संख्याको कोण निर्धारण गर्दछ, स्वचालित रूपमा यसलाई चार क्वाड्रन्टहरू मध्ये एकमा सहि राख्दछ।
तथापि, तन प्रयोग गरेर सावधान रहनुहोस्-1 कोण पत्ता लगाउन प्रकार्य, किनकि यो पहिलो र चौथो क्वाड्रन्टहरूमा मात्र returning ० –φ<90 °)।
देखि z1 समन्वय प्रणाली को पहिलो उद्धारकर्ता मा स्थित छ, गणना हो:
α 1 = तान्न-1(48 / 12) = तान्न-1(4) = 75.96 °
देखि z4 समन्वय प्रणाली, तनको तेस्रो चतुर्थार्थमा स्थित छ-1कोणलाई सही रूपमा फर्काउँदैन। कोण गणना:
α 4 = १°० ° + .180 75.96..255.96 ° 360 = २255.96..104.04 °-वा -XNUMX० ° + २XNUMX..XNUMX ° = - १०XNUMX.०XNUMX °, जुन टीआईएनए द्वारा गणना गरिएको जस्तै छ।
z2 समन्वय प्रणाली को चौथा चतुर्थार्थ मा स्थित छ कोण गणना:
α 2 = तान्न-1(-48 / 12) = तान्न-1(-4) = -75.96 °
z3, तथापि, समीकरण प्रणाली को 2nd चतुर्थार्थ मा छ, त त त-1 कोणलाई सही रूपमा फर्काउँदैन। कोण गणना:
α 3 = 180 ° -75.96 ° = 104.04 °।
उदाहरण 4 हामीसँग दुई जटिल संख्याहरू छन्: z1= 4 - j 6 र z2 = 5 ईj45 ° .
फेला z3 = z1 + z2; z4 = z1 - z2; z5 = z1 * z2; z6 = z1 / z2
पहिलो हामी TINA को अनुवादक को प्रयोग गरेर समस्या को हल
T TINA इंटरप्रिटर द्वारा समाधान} |
टिना कसरी विभिन्न ढाँचाहरूमा दुईवटा जटिल संख्याहरू ह्यान्डलले कसरी सँभाल्छ भनेर याद गर्नुहोस्।
दोभाषे बिना समाधान अधिक जटिल छ। ताकि हामी गुणन र भाग को बिभिन्न विधिहरु तुलना गर्न सक्दछौं, हामी पहिले ध्रुवीय रूप निर्धारण गर्नेछौं z1 र आयताकार रूप z2 .
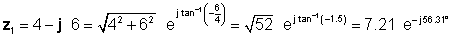
अर्को, हामी चार सजिलो फारमहरू प्रयोग गरेर पहिले समाधानहरू फेला पार्छौं: जोड र घटाउको लागि आयताकार, र गुणन र भागका लागि घाता :्क:
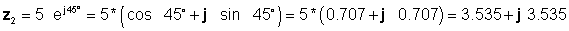
z 3 = z1 + z2 = 4 - j 6 + 3.535 + j 3.535 = 7.535 - j2.465
z 4 = z1 - z2 = 4 - j - - 6 - j 3.535 = 0.465 - j9.535
z 5 = z1 * z2 = 7.21 * 5 * ईj(-56.31 ° + 45 °) = 36.05 ई -j11.31 ° = 36.03 * (cos (-11.31 °) +j* पाप (-11.31 °))
z 5 = 35.33 - j 7.07
z 6 = z1/z2= (7.21 / 5) * ई j (-56.31 ° -45 °) = 1.442 ई - j 101.31 ° = 1.442 (cos (-101.31 °) +j* पाप (-101.31 °))
z 6 = -0.2828 - j 1.414
जो TINA ट्रान्सफर संग प्राप्त परिणाम संग सहमत छ।
गुणन आयताकार रूप मा गरियो:
z 5 =z1*z2 = (4-j6) * 3.535 * (1 +j) = 7.07 * (2-j3) * (1 +j) = 7.07 * (2-j3+j2 + 3) = 7.07 * (5-j) = 35.35-j7.07
अन्ततः विभाजन आयताकार रूप मा गरियो:
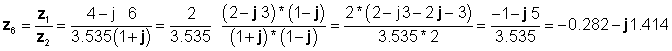
जुन अघिल्लो परिणामहरूसँग सहमत हुनुहोस्।

