Haga clic o toque los circuitos de ejemplo a continuación para invocar TINACloud y seleccione el modo DC interactivo para analizarlos en línea.
Haga clic o toque los circuitos de ejemplo a continuación para invocar TINACloud y seleccione el modo DC interactivo para analizarlos en línea. Obtenga un acceso de bajo costo a TINACloud para editar los ejemplos o crear sus propios circuitos
Otra forma de simplificar el conjunto completo de ecuaciones de Kirchhoff es el método actual de malla o bucle. Usando este método, la ley actual de Kirchhoff se satisface automáticamente, y las ecuaciones de bucle que escribimos también satisfacen la ley de voltaje de Kirchhoff. La ley actual de Kirchhoff se logra mediante la asignación de bucles de corriente cerrados llamados corrientes de malla o bucle a cada bucle independiente del circuito y el uso de estas corrientes para expresar todas las demás cantidades del circuito. Como las corrientes de bucle están cerradas, la corriente que fluye hacia un nodo también debe salir del nodo; entonces escribir ecuaciones de nodo con estas corrientes conduce a la identidad.
Consideremos primero el método de las corrientes de malla.
Primero notamos que el método de corriente de malla solo es aplicable para circuitos “planos”. Los circuitos planos no tienen cables cruzados cuando se dibujan en un plano. A menudo, al volver a dibujar un circuito que parece no ser plano, puede determinar que, de hecho, es plano. Para circuitos no planos, use el método de corriente de bucle Descrito más adelante en este capítulo.
Para explicar la idea de las corrientes de malla, imagine las ramas del circuito como "red de pesca" y asigne una corriente de malla a cada malla de la red. (A veces también se dice que se asigna un circuito de corriente cerrado en cada "ventana" del circuito).
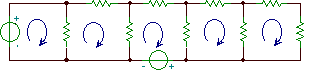  El diagrama esquematico   La “red de pesca” o la gráfica del circuito. |
La técnica de representar el circuito mediante un dibujo simple, llamado gráfica, es bastante poderoso Ya que Las leyes de Kirchhoff no dependen de la naturaleza de los componentes, puede ignorar los componentes de concreto y sustituirlos por segmentos de línea simples, llamados sucursales de la gráfica. Representar circuitos por gráficos nos permite usar las técnicas de matemática Teoría de grafos. Esto nos ayuda a explorar la naturaleza topológica de un circuito y determinar los bucles independientes. Regrese más tarde a este sitio para leer más sobre este tema.
Los pasos del análisis de la corriente de malla:
Asigne una corriente de malla a cada malla. Aunque la dirección es arbitraria, se acostumbra usar la dirección de las agujas del reloj.
Aplique la ley de voltaje de Kirchhoff (KVL) alrededor de cada malla, en la misma dirección que las corrientes de malla. Si una resistencia tiene dos o más corrientes de malla a través de ella, la corriente total a través de la resistencia se calcula como la suma algebraica de las corrientes de malla. En otras palabras, si una corriente que fluye a través de la resistencia tiene la misma dirección que la corriente de malla del bucle, tiene un signo positivo, de lo contrario, un signo negativo en la suma. Las fuentes de voltaje se tienen en cuenta como de costumbre, si su dirección es la misma que la corriente de malla, su voltaje se considera positivo, de lo contrario negativo, en las ecuaciones KVL. Por lo general, para las fuentes de corriente, solo una corriente de malla fluye a través de la fuente, y esa corriente tiene la misma dirección que la corriente de la fuente. Si este no es el caso, utilice el método de corriente de bucle más general, descrito más adelante en este párrafo. No es necesario escribir ecuaciones KVL para bucles que contienen corrientes de malla asignadas a fuentes actuales.
Resuelve las ecuaciones de bucle resultantes para las corrientes de malla.
Determine cualquier corriente o voltaje solicitado en el circuito utilizando las corrientes de malla.
Vamos a ilustrar El método por el siguiente ejemplo:
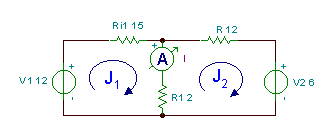
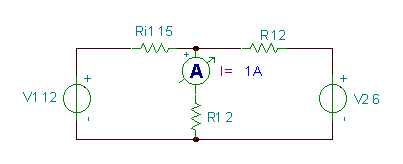
Encuentra la corriente I en el circuito de abajo.
Vemos que hay dos mallas (o una ventana izquierda y derecha) en este circuito. Asignemos las corrientes de malla en sentido horario J1 y J2 a las mallas. Luego escribimos las ecuaciones KVL, expresando los voltajes a través de las resistencias por la ley de Ohm:
-V1 + J1* (Ri1+R1) - J2*R1 = 0
V2 - J1*R1 + J2* (R + R1) = 0
Numéricamente:
-12 + J1* 17 - J2* 2 = 0
6 - J1* 2 + J2* 14 = 0
Expreso J1 de la primera ecuación: J1 = 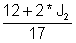

multiplicar por 17: 102 - 24 + 4 * J2 + 238 * J2 = 0 por lo tanto J2 = 
y J1 = 
Finalmente, la corriente requerida:
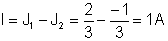
{Método actual de malla}
Sys J1, J2
J1*(Ri1+R1)-J2*R1-V1=0
J1*R1+J2*(R1+R)+V2=0
fin;
J1 = [666.6667m]
J2 = [- 333.3333m]
I: = J1-J2;
I = [1]
importar números como n
#¡Utilice el método actual de malla!
#Tenemos un sistema lineal de ecuaciones que queremos resolver.
#para I1,I2:
#I1*(Ri1+R1)+I2*Ri1-V1=0
#-V1+I1*Ri1+I2*(Ri1+R)+V2=0
#Escribe la matriz de los coeficientes:
A=n.array([[Ri1+R1,Ri1],[Ri1,Ri1+R]])
#Escribe la matriz de las constantes:
b=n.matriz([V1,V1-V2])
x=n.finalg.solve(A,b)
I1=x[0]
I2=x[1]
imprimir(“I1= %.3f”%I1)
imprimir(“I2= %.3f”%I2)
yo=yo1
imprimir(“Yo= %.3f”%Yo)
Veamos los resultados con TINA:

A continuación, resuelvamos el ejemplo anterior nuevamente, pero con el más general Método de las corrientes de bucle. Usando este método, los bucles de corriente cerrados, llamados corrientes de bucle, se asignan no necesariamente a las mallas del circuito, sino a arbitrarias bucles independientes. Puede asegurarse de que los bucles sean independientes teniendo al menos un componente en cada bucle que no esté contenido en ningún otro bucle. Para circuitos planos, el número de bucles independientes es el mismo que el número de mallas, lo cual es fácil de ver.
Una forma más precisa de determinar el número de bucles independientes es la siguiente.
Dado un circuito con b ramas y N nodos El número de los bucles independientes. l :
l = b - N + 1
Esto se deduce del hecho de que el número de ecuaciones de Kirchhoff independientes debe ser igual a las ramas en el circuito, y ya sabemos que solo hay N-1 Ecuaciones de nodos independientes. Por lo tanto, el número total de ecuaciones de Kirchhoff es
b = N-1 + l y por lo tanto l = b - N + 1
Esta ecuación también se desprende del teorema fundamental de la teoría de grafos que se describirá más adelante en este sitio.
Ahora resuelvamos el ejemplo anterior nuevamente, pero más simplemente, usando el método de corriente de bucle. Con este método somos libres de usar bucles en mallas o cualquier otro bucle, pero mantengamos el bucle con J1 en la malla izquierda del circuito. Sin embargo, para el segundo bucle, elegimos el bucle con J2, como se muestra en la figura a continuación. La ventaja de esta elección es que J1 será igual a la corriente solicitada I, ya que es la única corriente de bucle que pasa por R1. Esto significa que no necesitamos calcular J2 en absoluto. Tenga en cuenta que, a diferencia de las corrientes "reales", el significado físico de las corrientes de bucle depende de cómo las asignemos al circuito.
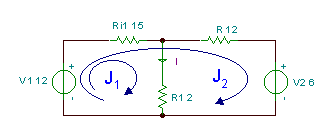

Las ecuaciones de KVL:
J1 * (R1+Ri1) + J2 * R i1 - V1 = 0
-V1+ J1 * Ri1+ J2 * (R + Ri) + V2 = 0
y la corriente requerida: I = J1
Numerically: J1*(15+2)+J2*15-12 = 0
-12 + J1 * 15 + J2 * (15 + 12) + 6 = 0
Exprese J2 de la segunda ecuación:
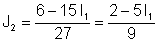
Sustituir en la primera ecuación:
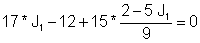
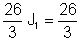
Por lo tanto: J1 = I = 1 A
Otros ejemplos.
ejemplo 1
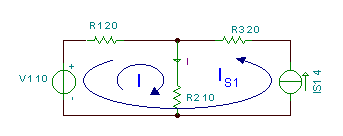
Encuentra la corriente I en el circuito de abajo.
En este circuito, utilizamos el método de las corrientes de bucle. En la ventana izquierda del circuito tomamos una corriente de bucle que denotamos con I ya que es igual a la corriente solicitada. La otra corriente de bucle es igual a la corriente de origen Is1, por lo que la denotamos directamente como IS1.
Tenga en cuenta que la dirección de esta corriente de bucle es no en el sentido de las agujas del reloj ya que su dirección está determinada por la fuente actual. Sin embargo, dado que esta corriente de bucle ya se conoce, no hay necesidad de escribir la ecuación KVL para el bucle donde IS1 se toma.
Por lo tanto, la única ecuación para resolver es:
-V1 + I * R2 + R1 * (Yo - yoS1) = 0
por lo tanto
Yo = (V1 + R1 *IS1) / (R1 + R2)
Numéricamente
I=(10+20*4)/(20+10)=3 A
También puede generar este resultado llamando al análisis simbólico de TINA desde el menú Análisis / Análisis simbólico / Resultado DC:
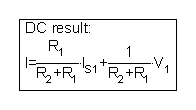
O puede resolver la ecuación KVL por el intérprete:
| {Solución del intérprete de TINA} {Usar el método de malla actual} Lo sys -V1 + I * R2 + R1 * (I - IS1) = 0 fin; I = [3] |
El siguiente ejemplo tiene 3 fuentes de corriente y es muy fácil de resolver por el método de las corrientes de bucle.
ejemplo 2
Encuentra el voltaje V.
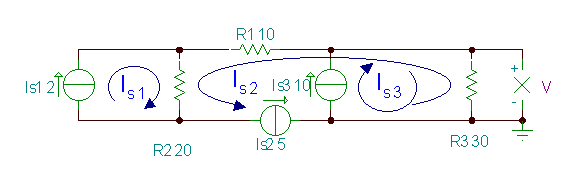

En este ejemplo, podemos elegir tres corrientes de bucle para que cada una pase a través de una sola fuente de corriente. Por lo tanto, se conocen las tres corrientes de bucle, y solo necesitamos expresar el voltaje desconocido, V, usándolas.
Haciendo la suma algebraica de las corrientes a través de R3:
V = (IS3 - YoS2) * R3= (10-5) * 30 = 150 V. Puede verificar esto con TINA :.
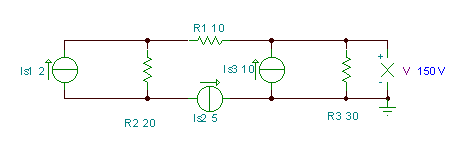

A continuación, abordemos nuevamente un problema que ya hemos resuelto en el Las leyes de kirchhoff y Método de potencial de nodo capítulos
ejemplo 3
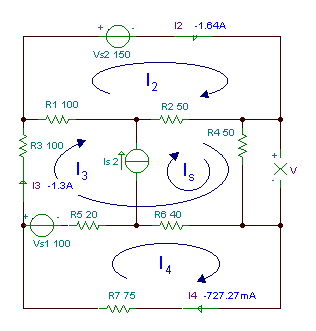
Encuentra la tensión V de la resistencia R4.
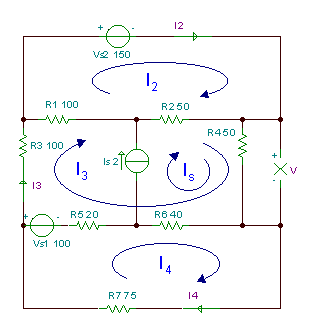

R1 = R3 = 100 ohm, R2 = R4 = 50 ohm, R5 = 20 ohm, R6 = 40 ohm, R7 = 75 ohm.
Este problema necesitaba al menos 4 ecuaciones para resolver en los capítulos anteriores.
Al resolver este problema con el método de las corrientes de bucle, tenemos cuatro bucles independientes, pero con la elección adecuada de las corrientes de bucle, una de las corrientes de bucle será igual a la corriente de la fuente Is.
Según las corrientes de bucle que se muestran en la figura anterior, las ecuaciones de bucle son:
VS1+I4* (R5+R6+R7) - YOS*R6 -YO3* (R5 + R6) = 0
VS2 - Yo3* (R1+R2) - YOS*R2 + I2* (R1 + R2) = 0
-VS1 + I3* (R1 + R2 + R3 + R4 + R5 + R6) + IS* (R2 +R4 + R6) - YO4* (R5 + R6) - Yo2* (R1 + R2) = 0
El voltaje desconocido V puede expresarse por las corrientes de bucle:
V = R4 * (YO2 + I3)
Numéricamente:
100 + I4* 135-2 * 40-I3* 60 = 0
150 + I2* 150-2 * 50-I3* 150 = 0
–100 + I3* 360 + 2 * 140-I4* 60-I2* 150 = 0
V = 50 * (2 + I3)
Podemos usar la regla de Cramer para resolver este sistema de ecuaciones:
I4 = D3/D
donde D es el determinante del sistema. D4, El determinante para I4, se forma sustituyendo el lado derecho del sistema se coloca por la columna de I4Los coeficientes.
El sistema de ecuaciones en forma ordenada:
- 60 * I3 + 135 * I4= -20
150 * I2-150 * I3 = - 50
-150 * I2+ 360 * I3 - 60 * I4= - 180
Entonces el determinante D:
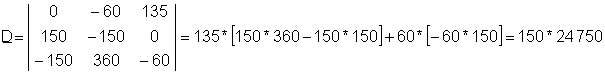
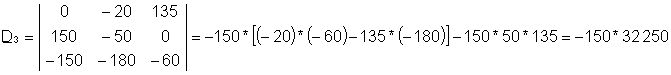
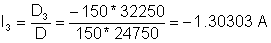
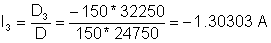
La solución de este sistema de ecuaciones es:
V = R4* (2 + I3) = 34.8485 V
Puede confirmar la respuesta a través del resultado calculado por TINA.
Sys I2, I3, I4
Vs2+I2*(R1+R2)-R2*Is-I3*(R1+R2)=0
-Vs1+I3*(R1+R2+R3+R4+R5+R6)+Is*(R2+R4+R6)-I2*(R1+R2)-I4*(R5+R6)=0
Vs1+I4*(R5+R6+R7)-Is*R6-I3*(R5+R6)=0
fin;
I2 = [- 1.6364]
I3 = [- 1.303]
I4 = [- 727.2727m]
V: = R4 * (Is + I3);
V = [34.8485]
importar números como n
#Tenemos un sistema lineal de ecuaciones que queremos resolver.
#para I1,I2,I3,I4:
#I1=Es
#Vs2+I2*(R1+R2)-R2*I1-I3*(R1+R2)=0
#-Vs1+I3*(R1+R2+R3+R4+R5+R6)+I1*(R2+R4+R6)-I2*(R1+R2)-I4*(R5+R6)=0
#Vs1+I4*(R5+R6+R7)-I1*R6-I3*(R5+R6)=0
#Escribe la matriz de los coeficientes:
A=n.array([[1,0,0,0],[-R2,R1+R2,-(R1+R2),0],[R2+R4+R6,-(R1+R2),R1+R2+R3+R4+R5+R6,-(R5+R6)],[-R6,0,-(R5+R6),R5+R6+R7]])
#Escribe la matriz de las constantes:
b=n.array([Es,-Vs2,Vs1,-Vs1])
x=n.finalg.solve(A,b)
I1,I2,I3,I4=x[0],x[1],x[2],x[3]
print(“I1= %.5f”%I1) #x[0]=I1
print(“I2= %.5f”%I2) #x[1]=I2
print(“I3= %.5f”%I3) #x[2]=I1
print(“I4= %.5f”%I4) #x[3]=I2
V=R4*(I1+I3)
imprimir(“V= %.5f”%V)
En este ejemplo, cada corriente de bucle desconocida es una corriente de derivación (I1, I3 e I4); por lo tanto, es fácil verificar el resultado en comparación con los resultados del análisis DC de TINA.