 Kliknite alebo ťuknite na nižšie uvedené okruhy príkladov, aby ste vyvolali TINACloud a vyberte režim Interaktívny DC na analýzu online.
Kliknite alebo ťuknite na nižšie uvedené okruhy príkladov, aby ste vyvolali TINACloud a vyberte režim Interaktívny DC na analýzu online. Získajte lacný prístup k TINACloudu na úpravu príkladov alebo vytvorenie vlastných okruhov
V tejto a nasledujúcich kapitolách predstavíme veľmi dôležitú tému: AC alebo striedavý prúd. Názov striedavého prúdu nie je veľmi presný a bežne pokrýva obvody so sínusovými napätiami a prúdmi; striedavý prúd však môže tiež znamenať ľubovoľný ľubovoľný priebeh prúdu. Význam striedavého napätia spočíva v tom, že tento druh napätia sa používa pre hlavný zdroj elektrickej energie v domácnostiach a priemysle na celom svete. Je tiež základom mnohých elektronických, telekomunikačných a priemyselných aplikácií.
Na spracovanie sínusových priebehov a obvodov s nimi spojených budeme používať jednoduchú a elegantnú metódu nazývanú metódu fázorov. Fázory sú založené na vlastnostiach komplexných čísel, ktoré sú ideálne pre reprezentáciu sínusových veličín. V tejto kapitole zhrnieme základné fakty o komplexných číslach a ich fungovaní. Ukážeme tiež, ako tlmočník TINA uľahčuje výpočty s komplexnými číslami.
Komplexné čísla sa skladajú z dvoch častí, a skutočná časť (x), čo je skutočné číslo a tzv imaginárnej časti (y), čo je reálne číslo vynásobené 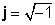
z = x + jy
kde 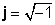
Príklady komplexných čísel:
z 1 = 1 + j
z 2 = 4-2 j
z 3 = 3- 5j
Komplexné čísla boli pôvodne zavedené v sedemnástom storočí, aby predstavovali korene polynómov, ktoré nemohli byť zastúpené iba reálnymi číslami. Napríklad korene rovnice x2 + 2x + 2 = 0 môže byť opísaný len ako 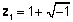
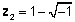
Geometrická reprezentácia komplexných čísel
Obdĺžnikový tvar
Pretože komplexné číslo sa dá vždy rozdeliť na jeho skutočnú a zložitú časť, môžeme reprezentovať komplexné číslo ako bod v dvojrozmernej rovine. Reálna časť komplexného čísla je projekcia bodu na skutočnú os a imaginárna časť čísla je projekcia na imaginárnu os. Keď je komplexné číslo reprezentované ako súčet skutočných a imaginárnych častí, hovoríme, že je v obdĺžnikový or algebraická forma.
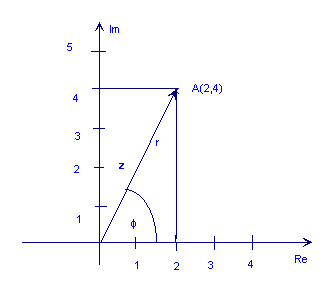
Nasledujúci obrázok zobrazuje komplexné číslo z = 2 + 4j
Polárna a exponenciálna forma
Ako vidíte na obrázku vyššie, bod A môže byť tiež reprezentovaný dĺžkou šípky, r (nazýva sa aj absolútna hodnota, veľkosť alebo amplitúda) a jeho uhol (alebo fáza), φ relatívne proti smeru hodinových ručičiek k pozitívnej horizontálnej osi. To je polárne forma komplexného čísla. Označuje sa ako r ∠ φ.
Ďalší krok je veľmi dôležitý. Komplexné číslo v polárnej forme môže byť tiež zapísané exponenciálny forma:
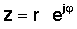
Tento jednoduchý výraz je charakteristický tým, že má pomyselné číslo v exponente namiesto zvyčajného reálneho čísla. Tento komplexný exponenciál sa správa veľmi odlišne od exponenciálnej funkcie so skutočným argumentom. Zatiaľ čo ex rastie rýchlo vo veľkosti pre zväčšenie x> 0 a klesá pre x <0, funkcia 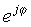
Eulerov vzorec poskytuje zjednocujúci vzťah medzi obdĺžnikovými, polárnymi a exponenciálnymi formami komplexných čísel:
z = x + jy = re jφ = r (cos φ + j hriech φ )
kde 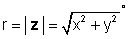
a φ = opálenie-1 (Y / x).
Pre náš vyššie uvedený príklad z = 2 + 4j:
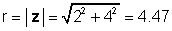
φ = opálenie-1 (4 / 2) = 63.4 °
teda 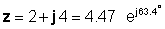
Alebo naopak:
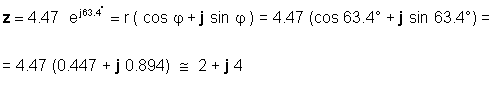
V závislosti od aplikácie budete musieť byť oboznámený s používaním oboch formulárov. Napríklad sa sčítanie alebo odčítanie očividne ľahšie robí, keď sú čísla v pravouhlej forme, zatiaľ čo násobenie a delenie sa ľahšie robia, keď sú čísla v exponenciálnej forme.
Operácie s komplexnými číslami
Operácie, ktoré sa dajú robiť s komplexnými číslami, sú podobné ako pri reálnych číslach. Pravidlá a niektoré nové definície sú zhrnuté nižšie.
Operácie s j
Operácie s j jednoducho vychádzať z definície imaginárnej jednotky,


Aby ste mohli pracovať rýchlo a presne, mali by ste si tieto pravidlá zapamätať:
j 2 = -1
j 3 =-j
j 4 =1
1/j = -j
j2 = -1 jednoducho vyplýva z definície 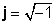
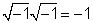
Pre 1 /j, násobíme 1 /jby j / j = 1 a získajte j/ (J J) = j / (- 1) = -j.
Komplexný konjugát
Komplexný konjugát komplexného čísla je ľahko odvoditeľný a je veľmi dôležitý. Na získanie komplexného konjugátu komplexného čísla v obdĺžnikovej forme jednoducho zmeňte znak imaginárnej časti. Ak chcete tak urobiť pre číslo v exponenciálnom tvare, zmeňte znamienko uhlu komplexného čísla pri zachovaní jeho absolútnej hodnoty.
Komplexný konjugát komplexného čísla z sa často označuje ako z*.
Vzhľadom na komplexné číslo z= A + jb, jeho komplexný konjugát je z*= a- jb.
If z sa uvádza v exponenciálnej forme, 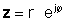
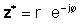
Pomocou vyššie uvedených definícií je ľahké vidieť, že komplexné číslo vynásobené komplexným konjugátom dáva štvorcu absolútnej hodnoty komplexného čísla:
zz* = r2 = a2 + b2
Pridaním alebo odčítaním akéhokoľvek komplexného čísla a jeho konjugátu dostaneme nasledujúce vzťahy:
z + z * = 2a
teda
Re (z) = a = ( z + z * ) / 2
podobne:
z - z * =j2b
teda
im (z) = b = ( z -z * ) / 2j
Dôkaz:
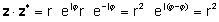
alebo násobenie skutočných a imaginárnych častí a použitie j2= -1
zz* = (A + jb) (a - jb) = a2+a jb - a jb - jbjb = a2j2 = a2 + b2
z + z* = A + jb + a - jb = 2a
z - z*= A + jb - a + jb =j2b
Numerické príklady:
V obdĺžnikovom tvare:
z = 3 + j4
z* = 3- j4
zz * = 9 + 16 = 25
V polárnej forme
z = 5 ∠ 53.13 °
z * = 5 - 53.13 °
V exponenciálnej forme:
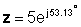
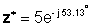
Sčítanie a odčítanie
Sčítanie a odčítanie komplexných čísel je jednoduché - stačí len pridať skutočnú a imaginárnu časť osobitne. Napríklad, ak
z1 = 3 - 4j a z2 = 2 + 3j
potom
z1 + z2 = 3 - 4j + 2 + 3j = 3 + 2 - 4j + 3j = 5 - j
z1 - z2 = 3 - 4j - 2 - 3j = 3 - 2 - 4j - 3j = 1 - j7
Je zrejmé, že na tieto operácie by sme mali používať pravouhlý tvar. Ak sú čísla uvedené v exponenciálnej alebo polárnej forme, mali by sme ich najprv transformovať na pravouhlú formu pomocou Eulerovho vzorca, ako je uvedené vyššie.
Násobenie
Existujú dve metódy na násobenie komplexných čísel -
Násobenie komplexných čísel v obdĺžnikovej forme
Na vykonanie operácie jednoducho vynásobte reálne a imaginárne časti jedného čísla reálnymi a imaginárnymi časťami druhého čísla a použite identitu j2 = -1.
z1z2 = (a1 + jb1) (a2 + jb2) = a1 a2 + jb1a2+ jb2a1 - b1b2 = a1 a2- b1b2 + j(b1a2+ jb2a1)
Keď sú komplexné čísla uvedené číselne, nie je potrebné použiť vyššie uvedený vzorec. Napríklad, nech
z1 = 3 - 4j a z2 = 2 + 3j
S priamym násobením komponentov:
z1z2 = (3 - 4j) (2 + 3j) = 6-8j +9j + 12 = 18 + j
alebo pomocou vzorca: z1z2 = a1 a2- b1b2 + j(b1a2+ b2a1)
z1z2 = 6 + 12 + j (-8 + 9) = 18 + j
Myslíme si, že ak použijete vzorec, je pravdepodobnejšie, že urobíte chybu, ak komponenty vynásobíte priamo.
z1: = 3-4 * j
z2: = 2 + 3 * j
z1 * z2 = [18 + 1 * j]
importovať matematiku ako m
importovať cmath ako c
z1=komplex('3-4j')
z2=komplex('2+3j')
print(“z1*z2=”,z1*z2)
Násobenie komplexných čísel v polárnej alebo exponenciálnej forme
Na vykonanie tejto operácie vynásobte absolútne hodnoty a pridajte uhly dvoch komplexných čísel. nech:
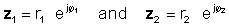
Potom pomocou pravidla násobenia exponenciálnych funkcií:
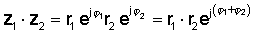
alebo v polárnej forme
z1 z2 = r1 r2 ∠ φ1 + φ2
Poznámka: Toto pravidlo sme už použili pri výpočte zz *vyššie. Pretože uhol konjugátu má opačné znamienko ako pôvodný uhol, komplexné číslo vynásobené jeho vlastným konjugátom je vždy skutočné číslo; a to druh štvorca jeho absolútnej hodnoty: zz * = r2
Napríklad:
z1 = 5 ° 30 ° a z2 = 4 ° -60 °
potom
z1z2 = 20 ° -30 °
alebo v exponenciálnej forme
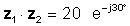
Násobenie je zjavne jednoduchšie, keď sú čísla v polárnej alebo exponenciálnej forme.
Ak sú však komplexné čísla uvedené v obdĺžnikovej podobe, mali by ste zvážiť vykonanie násobenia priamo tak, ako je to znázornené vyššie, pretože ak tieto čísla prevádzate do polárnej formy pred ich násobením, je potrebné vykonať ďalšie kroky. Ďalším faktorom, ktorý treba zvážiť, je, či chcete, aby boli odpovede v obdĺžnikovej forme alebo v polárnej / exponenciálnej podobe. Napríklad, ak sú tieto dve čísla v obdĺžnikovej forme, ale chceli by ste, aby ich produkt bol v polárnej forme, má zmysel okamžite ich previesť a potom ich množiť.
delenie
Existujú dve metódy na rozdelenie komplexných čísel -
Rozdelenie komplexných čísel v obdĺžnikovom tvare
Ak chcete vykonať operáciu, vynásobte čitateľa a menovateľa konjugátom menovateľa. Menovateľ sa stáva skutočným číslom a delenie sa zníži na násobenie dvoch komplexných čísel a delenie skutočným číslom, štvorcom absolútnej hodnoty menovateľa.
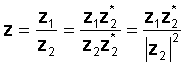
Napríklad:
z1 = 3 - 4j a z2 = 2 + 3j
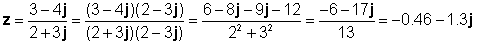
Skontrolujme tento výsledok pomocou tlmočníka TINA:
z1: = 3-4 * j
z2: = 2 + 3 * j
z1 / z2 = [- 461.5385-1.3077 * j]
importovať matematiku ako m
importovať cmath ako c
z1=komplex('3-4j')
z2=komplex('2+3j')
print(“z1/z2=”,z1/z2)
Rozdelenie komplexných čísel v polárnej alebo exponenciálnej forme
Na vykonanie operácie rozdeliť absolútne hodnoty (veličiny) a odčítať uhol menovateľa od uhla čitateľa. nech:
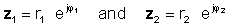
potom pomocou pravidla rozdelenia exponenciálnych funkcií
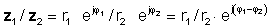
alebo v polárnej forme
z 1 / z2 = r1 / r2 ∠ φ 1- φ 2
Napríklad:
z 1 = 5 ∠ 30 ° a z 2 = 2 ∠ -60 °
potom
z 1 / z2 = 2.5 ∠ 90 °
alebo v exponenciálnych a obdĺžnikových formách
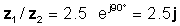
Skontrolujme tento výsledok pomocou tlmočníka TINA:
z1: = 5 * exp (j * degtorad (30))
z2: = 2 * exp (j * degtorad (-60))
z1 / z2 = [0 + 2.5 * j]
importovať matematiku ako m
importovať cmath ako c
z1=5*(c.exp(komplex(0,m.radiánov(30))))
z2=2*(c.exp(komplex(0,m.radiánov(-60))))
print(“z1/z2=”,z1/z2)
Rozdelenie je samozrejme jednoduchšie, ak sú čísla v polárnej alebo exponenciálnej podobe.
Ak sú však komplexné čísla uvedené v obdĺžnikovej forme, mali by ste zvážiť vykonanie delenia priamo pomocou metódy komplexného konjugátu, ako je to znázornené vyššie, pretože pred rozdelením čísel na polárne tvary existujú ďalšie kroky. Ďalším faktorom, ktorý treba zvážiť, je, či chcete, aby boli odpovede v obdĺžnikovej forme alebo v polárnej / exponenciálnej podobe. Napríklad, ak sú tieto dve čísla v obdĺžnikovej forme, ale chceli by ste, aby ich kvocient bol v polárnej forme, má zmysel ich okamžite previesť a potom ich rozdeliť.
Teraz ilustrujme použitie komplexných čísel viacerými numerickými problémami. Ako zvyčajne, naše riešenia skontrolujeme pomocou tlmočníka TINA. Tlmočník pracuje s radiánmi, ale má štandardné funkcie pre konverziu radiánov na stupne alebo naopak.
Príklad 1 Nájdite polárnu reprezentáciu:
z = 12 - j 48
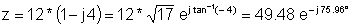
z: = 12-j * 48;
abs (z) = [49.4773]
oblúk (z) = [- 1.3258]
radtodeg (oblúk (z)) = [- 75.9638]
importovať matematiku ako m
importovať cmath ako c
z=12-komplex(48j)
print(“abs(z)=”,abs(z))
print(“arc(z)=”,c.phase(z))
print(“stupne(oblúk(z))=”,m.stupne(c.fáza(z)))
Príklad 2 Nájsť obdĺžnikové zobrazenie:
z = 25 e j 125 °
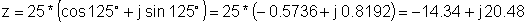
z: = 25 * exp (j * (degtorad (125)));
z = [- 14.3394 + 20.4788 * j]
Re (z) = [- 14.3394]
Im (z) = [20.4788]
importovať matematiku ako m
importovať cmath ako c
z=25*c.exp(komplex(0,m.radiánov(125)))
vytlačiť(“z=”,z)
print(“real(z)=”,z.real)
print(“imag(z)=”,z.imag)
Príklad 3 Nájdite polárnu reprezentáciu nasledujúcich komplexných čísel:
z 1 = 12 + j 48 z2 = 12 - j48 z3= -12 + j 48 z4= -12 - j 48
Absolútne hodnoty všetkých štyroch čísel sú rovnaké, pretože absolútna hodnota je nezávislá od znakov. Iba uhly sú rôzne.
z1: = 12 + j * 48;
abs (z1) = [49.4773]
oblúk (z1) = [1.3258]
radtodeg (oblúk (z1)) = [75.9638]
z2: = 12-j * 48;
abs (z2) = [49.4773]
oblúk (z2) = [- 1.3258]
radtodeg (oblúk (z2)) = [- 75.9638]
z3: = - 12 + j * 48;
abs (z3) = [49.4773]
oblúk (z3) = [1.8158]
radtodeg (oblúk (z3)) = [104.0362]
z4: = - 12-j * 48:
abs (z4) = [49.4773]
oblúk (z4) = [- 1.8158]
radtodeg (oblúk (z4)) = [- 104.0362]
importovať matematiku ako m
importovať cmath ako c
z1=komplex('12+48j')
print(“abs(z1)=”,abs(z1))
print(“arc(z1)=”,c.phase(z1))
print(“stupne(oblúk(z1))=”,m.stupne(c.fáza(z1)))
z2=komplex('12-48j')
print(“abs(z2)=”,abs(z2))
print(“arc(z2)=”,c.phase(z2))
print(“stupne(oblúk(z2))=”,m.stupne(c.fáza(z2)))
z3=komplex('-12+48j')
print(“abs(z3)=”,abs(z3))
print(“arc(z3)=”,c.phase(z3))
print(“stupne(oblúk(z3))=”,m.stupne(c.fáza(z3)))
z4=komplex('-12-48j')
print(“abs(z4)=”,abs(z4))
print(“arc(z4)=”,c.phase(z4))
print(“stupne(oblúk(z4))=”,m.stupne(c.fáza(z4)))
Funkcia arc () TINA určuje uhol ľubovoľného komplexného čísla a automaticky ho správne umiestni do jedného zo štyroch kvadrantov.
Dávajte si však pozor na opálenie-1 funkcia na vyhľadanie uhla, pretože je obmedzená na návratové uhly iba v prvom a štvrtom kvadrante (–90 °φ<90 °).
Od z1 sa nachádza v prvom kvadrante súradnicového systému, výpočet je:
α 1 = opálenie-1(48 / 12) = opálenie-1(4) = 75.96 °
Od z4 sa nachádza v treťom kvadrante súradnicového systému, tan-1nevracia správne uhol. Výpočet uhla je:
α 4 = 180 ° + 75.96 ° = 255.96 ° alebo -360 ° + 255.96 ° = - 104.04 °, čo je rovnaké ako pri výpočte TINA.
z2 sa nachádza vo štvrtom kvadrante súradnicového systému Výpočet uhla je:
α 2 = opálenie-1(-48 / 12) = tan-1(-4) = -75.96 °
z3, je však v kvadrante 2nd súradnicového systému, takže tan-1 nevracia správne uhol. Výpočet uhla je:
α 3 = 180 ° -75.96 ° = 104.04 °.
Príklad 4 Máme dve komplexné čísla: z1= 4 - j 6 a z2 = 5 ej45 ° .
nájsť z3 = z1 + z2; z4 = z1 - z2; z5 = z1 * z2; z6 = z1 / z2
Najprv riešime problém pomocou tlmočníka TINA
{Riešenie od tlmočníka TINA} |
Všimnite si, ako TINA ľahko zvláda dve komplexné čísla uvedené v rôznych formách.
Riešenie je zložitejšie bez tlmočníka. Aby sme mohli porovnávať rôzne metódy násobenia a delenia, najskôr určíme polárnu formu z1 a obdĺžniková forma z2 .
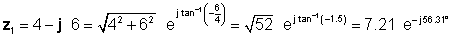
Ďalej najskôr nájdeme štyri riešenia, ktoré používajú najjednoduchšie formy: pravouhlý pre sčítanie a odčítanie a exponenciálny pre násobenie a delenie:
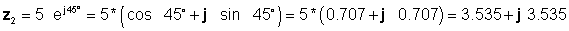
z 3 = z1 + z2 = 4 - j 6 + 3.535 + j 3.535 = 7.535 - j2.465
z 4 = z1 - z2 = 4 - j 6 - 3.535 - j 3.535 = 0.465 - j9.535
z 5 = z1 * z2 = 7.21 * 5 * ej(-56.31 ° + 45 °) = 36.05 e -j11.31 ° = 36.03 * (cos (-11.31 °) +)j* sin (-11.31 °))
z 5 = 35.33 - j 7.07
z 6 = z1/z2= (7.21 / 5) * e j (-56.31 ° -45 °) = 1.442 e - j 101.31 ° = 1.442 (cos (-101.31 °) +)j* sin (-101.31 °))
z 6 = -0.2828 - j 1.414
ktoré súhlasia s výsledkami získanými s tlmočníkom TINA.
Násobenie vykonané v obdĺžnikovom tvare:
z 5 =z1*z2 = (4-j6) * 3.535 * (1 +j) = 7.07 * (2-j3) * (1 +j) = 7.07 * (2-j3+j2 + 3) = 7.07 * (5-j) = 35.35-j7.07
Nakoniec rozdelenie vykonané v obdĺžnikovom tvare:
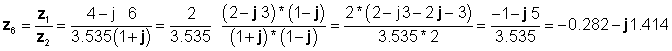
ktoré súhlasia s predchádzajúcimi výsledkami.

