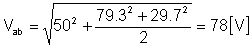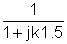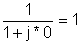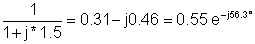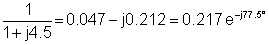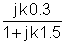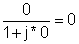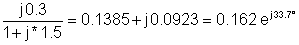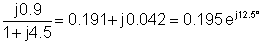Clique ou toque nos circuitos de exemplo abaixo para chamar o TINACloud e selecione o modo CC interativo para analisá-los on-line.
Obtenha um acesso de baixo custo ao TINACloud para editar os exemplos ou criar seus próprios circuitos

A Teorema de Fourier afirma que qualquer forma de onda periódica pode ser sintetizada adicionando termos seno e cosseno adequadamente ponderados de várias frequências. O teorema é bem abordado em outros livros didáticos, portanto iremos apenas resumir os resultados e mostrar alguns exemplos.

Deixe nossa função periódica ser f (t) = f (t ±nT) onde T é o tempo de um período en é um número inteiro.

w₀= 2p/ t a frequência angular fundamental.

Pelo Teorema de Fourier, a função periódica pode ser escrita como a seguinte soma:

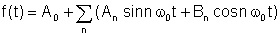
onde

A_n e B_n são as Coeficientes de Fourier e a soma é a Séries de Fourier.

Outra forma, provavelmente um pouco mais prática:

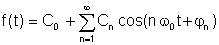
onde

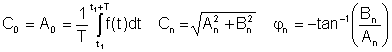
A₀ = C₀ é o DC ou valor médio, A₁, B₁ e C₁ são os componentes fundamentais e os demais são os termos harmônicos.

Embora apenas alguns termos possam ser necessários para aproximar algumas formas de onda, outros exigirão muitos termos.

Geralmente, quanto mais termos incluídos, melhor será a aproximação, mas para formas de onda contendo passos, como impulsos retangulares, o Fenômeno de Gibbs entra em jogo. À medida que o número de termos aumenta, o overshoot concentra-se num período de tempo cada vez menor.

An função par f(t) = f(-t) (simetria do eixo) requer apenas termos de cosseno.

An Função estranha f(t) = – f(-t) (simetria de ponto) requer apenas termos senoidais.

Uma forma de onda com simetria em espelho ou em meia onda tem apenas estranho harmônicos em sua representação de Fourier.

Aqui não trataremos da expansão em série de Fourier, mas usaremos apenas uma dada soma de senos e cossenos como excitação para um circuito.

Nos capítulos anteriores deste livro, tratamos da excitação sinusoidal. Se o circuito for linear, o Teorema da superposição é válido. Para uma rede com excitação periódica não senoidal, a superposição nos permite calcule as correntes e tensões devidas a cada termo senoidal de Fourier, um de cada vez. Quando todos são calculados, finalmente resumimos os componentes harmônicos da resposta.

É um pouco complicado determinar os diferentes termos das tensões e correntes periódicas e, de fato, pode gerar uma sobrecarga de informações. Na prática, gostaríamos simplesmente de fazer medições. Podemos medir os diferentes termos harmônicos usando um analisador harmônico, analisador de espectro, analisador de ondas ou analisador de Fourier. Todos estes são complicado e provavelmente produz mais dados do que o necessário. Às vezes é suficiente descrever um sinal periódico apenas pelos seus valores médios. Mas existem vários tipos de medidas médias.

MÉDIA VALORES

Média simples or DC termo foi visto na representação de Fourier como A₀

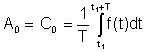
Esta média pode ser medida com instrumentos como o Deprez Instrumentos DC.

Valor efetivo or rms (raiz quadrada média) tem a seguinte definição:

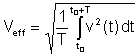
Este é o valor médio mais importante porque o calor dissipado nos resistores é proporcional ao valor efetivo. Muitos voltímetros digitais e alguns analógicos podem medir o valor efetivo de tensões e correntes.

Média absoluta

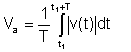
Esta média já não é importante; instrumentos anteriores mediam esta forma de média.

Se conhecermos a representação de Fourier de uma forma de onda de tensão ou corrente, também podemos calcular os valores médios da seguinte forma:

Média simples or DC termo foi visto na representação de Fourier como A₀ = C₀

Valor efetivo or rms (raiz quadrada média) é, depois de integrar a série de Fourier da tensão:

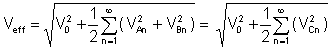
A fator klirr é uma proporção muito importante dos valores médios:

É a razão entre o valor efetivo dos termos harmônicos superiores ao valor efetivo do harmônico fundamental:

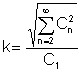
Parece haver uma contradição aqui – resolvemos a rede em termos de componentes harmônicos, mas medimos quantidades médias.

Vamos ilustrar o método com exemplos simples:

Exemplo 1

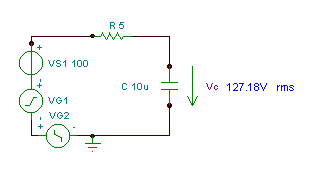
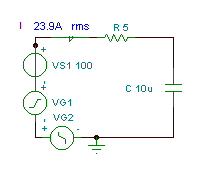
Encontre a função de tempo e o valor efetivo (rms) da tensão v_C(T)

se R = 5 ohm, C = 10 mF e v (t) = (100 + 200 cos (w₀t) + 30 cos (3 w₀t - 90 °)) V, onde a frequência angular fundamental é w₀= 30 krad / s.

Tente usar o teorema da superposição para resolver o problema.

O primeiro passo é encontrar a função de transferência em função da frequência. Para simplificar, use a substituição: s = j w

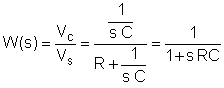
Agora substitua os valores dos componentes e s = jk w₀onde k = 0; 1; 3 neste exemplo e w₀= 30 krad/s. Em V, A, ohm mUnidades F e Mrad / s:

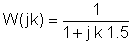
É útil usar uma tabela para organizar as etapas da solução numérica:

Podemos resumir as etapas da solução da superposição em outra tabela. Como já vimos, para encontrar o valor de pico complexo de um componente, devemos multiplicar o valor de pico complexo do componente da excitação pelo valor da função de transferência complexa:

E finalmente podemos fornecer a função tempo conhecendo os valores de pico complexos dos componentes:

v_C(t) = 100 + 110 cos(w₀t - 56.3°) + 6.51 cos (3w₀t - 167.5°) V

O valor rms (efetivo) da tensão é:

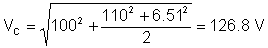
Como você pode ver, o instrumento de medição da TINA mede esse valor rms.

Exemplo 2

Encontre a função tempo e o valor efetivo (rms) da corrente i(t)

se R = 5 ohm, C = 10 mF e v (t) = (100 + 200 cos (w₀t) + 30 cos (3w₀t - 90 °)) V onde a frequência angular fundamental é w₀= 30 krad / s.

Tente resolver o problema usando o teorema da superposição.

As etapas da solução são semelhantes ao Exemplo 1, mas a função de transferência é diferente.

Agora substitua os valores numéricos e s = jk w_0,onde k = 0; 1; 3 neste exemplo.

Em V, A, ohm mUnidades F e Mrad / s:

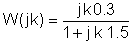
É útil usar uma tabela durante a solução numérica:

Podemos resumir as etapas da superposição em outra tabela. Como já vimos, para encontrar o valor de pico de uma componente, devemos multiplicar o valor de pico complexo dessa componente da excitação pelo valor da função de transferência complexa. Use os valores de pico complexos dos componentes da excitação:

E finalmente, conhecendo os valores de pico complexos dos componentes, podemos enunciar a função tempo:

i (t) = 32.4 cos (w₀t + 33.7°) + 5.85 cos (3w₀t - 77.5°) [UMA]

TO valor rms da corrente:

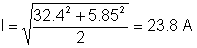
Muitas vezes você pode fazer uma verificação de integridade de parte da solução. Por exemplo, um capacitor pode ter uma tensão CC, mas não uma corrente CC.

Exemplo 3

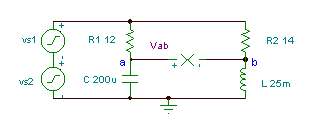
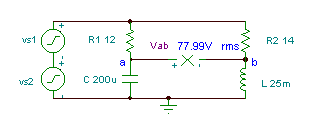
Obtenha a função tempo da tensão V_ab if R₁= 12 ohm, R₂ = 14 ohms, L = 25 mH e

C = 200 mF. A tensão do gerador é v(t)=(50 + 80 cos(w₀t) + 30 cos (2 w₀t + 60 °)) V, onde a frequência fundamental é f₀ = 50 Hz.

O primeiro passo é encontrar a função de transferência:

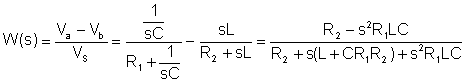
Substituindo valores numéricos em unidades V, A, ohm, mH, mF, kHz:

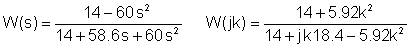
Mesclando as duas tabelas:

k V Sk		V abk
0 50		50
1 80		79.3 de-j66.3
2 30 ej60		29.7 de-j44.7

Finalmente a função de tempo:

v_ab(t) = 50 + 79.3 cos (w₁t - 66.3°) + 29.7 cos (2w₁t - 44.7°) [V]

e o valor eficaz:

---