Clique ou toque nos circuitos de exemplo abaixo para chamar o TINACloud e selecione o modo CC interativo para analisá-los on-line.
Clique ou toque nos circuitos de exemplo abaixo para chamar o TINACloud e selecione o modo CC interativo para analisá-los on-line. Obtenha um acesso de baixo custo ao TINACloud para editar os exemplos ou criar seus próprios circuitos
Uma tensão sinusoidal pode ser descrita pela equação:
v (t) = VM sin (ωt + Φ) ou v (t) = VM cos (ωt + Φ)
| onde | v (t) | Valor instantâneo da tensão, em volts (V). |
| VM | Valor máximo ou máximo da tensão, em volts (V) | |
| T | Período: o tempo gasto por um ciclo, em segundos | |
| f | Freqüência - o número de períodos em segundo 1, em Hz (Hertz) ou 1 / s. f = 1 / T | |
| ω | Freqüência angular, expressa em radianos / s ω = 2 * π * f ou ω = 2 * π / T. | |
| Φ | Fase inicial dada em radianos ou graus. Essa quantidade determina o valor da onda senoidal ou cosseno att = 0. | |
| Nota: A amplitude de uma tensão senoidal é algumas vezes expressa como VEff, o valor efetivo ou RMS. Isto está relacionado com VM de acordo com o relacionamento VM= √2VEf, ou aproximadamente VEff = 0.707 VM |
Aqui estão alguns exemplos para ilustrar os termos acima.
As propriedades da tensão 220 V AC em tomadas elétricas domésticas na Europa:
Valor efetivo: VEff = 220 V
Valor de pico: VM= √2 * 220 V = 311 V
Freqüência: f = 50 1 / s = 50 Hz
Frequência angular: ω = 2 * π * f = 314 1 / s = 314 rad / s
Período: T = 1 / f = 20 ms
Função de tempo: v (t) = 311 sen (314 t)
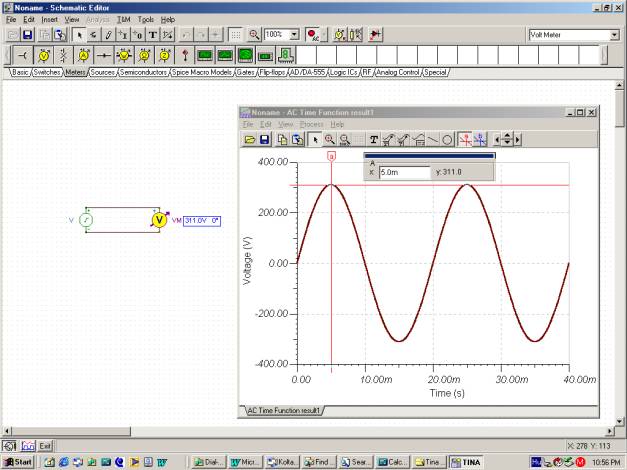
Vamos ver a função time usando o comando Analysis / AC Analysis / Time Function do TINA.
Você pode verificar se o período é T = 20m e que VM = 311 V.
As propriedades da tensão 120 V AC na tomada elétrica doméstica nos EUA:
Valor efetivo: VEff = 120 V
Valor de pico: VM= 2 120 V = 169.68 V 170 V
Freqüência: f = 60 1 / s = 60 Hz
Frequência angular: ω = 2 * π * f = 376.8 rad / s ≈ 377 rad / s
Período: T = 1 / f = 16.7 ms
Função de tempo: v (t) = 170 sen (377 t)
Note que neste caso a função tempo poderia ser dada como v (t) = 311 sen (314 t + Φ) ou v (t) = 311 cos (314 t + Φ), já que no caso da tensão de saída nós Não conheço a fase inicial.
A fase inicial desempenha um papel importante quando várias voltagens estão presentes simultaneamente. Um bom exemplo prático é o sistema trifásico, onde três tensões do mesmo valor de pico, forma e frequência estão presentes, cada uma com uma mudança de fase 120 ° em relação às outras. Numa rede 60 Hz, as funções de tempo são:
vA(t) = 170 sen (377 t)
vB(t) = 170 sen (377 t - 120 °)
vC(t) = 170 sen (377 t + 120 °)
A figura a seguir feita com TINA mostra o circuito com essas funções de tempo como geradores de tensão da TINA.
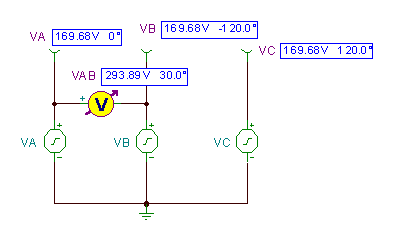

A diferença de tensão vAB= vA(televisãoB(t) é mostrado como resolvido pelo comando Analysis / AC Analysis / Time Function da TINA.
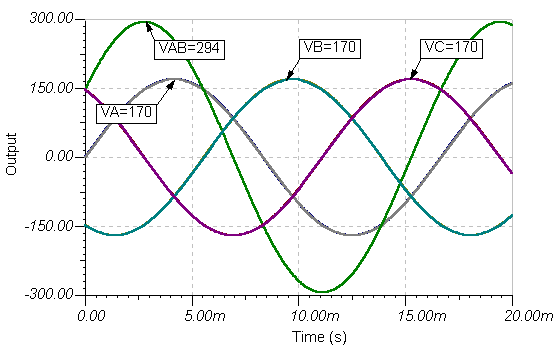

Note que o pico de vAB (t) é aproximadamente 294 V, maior que os picos 170 V doA(t) ou vB(t) tensões, mas também não simplesmente a soma de suas tensões de pico. Isto é devido à diferença de fase. Vamos discutir como calcular a tensão resultante (que é Ö3 * 170 @ 294, neste caso) mais adiante neste capítulo e também no Sistemas trifásicos capítulo.
Valores característicos de sinais sinusoidais
Embora um sinal AC varie continuamente durante seu período, é fácil definir alguns valores característicos para comparar uma onda com outra: estes são os valores de pico, média e média quadrática (rms).
Nós já conhecemos o valor máximo VM , que é simplesmente o valor máximo da função do tempo, a amplitude da onda sinusoidal.
Às vezes, o valor pico a pico (pp) é usado. Para tensões e correntes senoidais, o valor pico a pico é o dobro do valor máximo.
A valor médio da onda senoidal é a média aritmética dos valores para o meio ciclo positivo. Também é chamado média absoluta já que é igual à média do valor absoluto da forma de onda. Na prática, encontramos essa forma de onda retificando a onda senoidal com um circuito chamado retificador de onda completa.
Pode ser mostrado que a média absoluta de uma onda sinusoidal é:
VAV= 2 / π VM ≅ 0.637 VM
Observe que a média de um ciclo inteiro é zero.
O valor eficaz ou efetivo de uma tensão ou corrente sinusoidal corresponde ao valor CC equivalente, produzindo a mesma potência de aquecimento. Por exemplo, uma voltagem com um valor efetivo de 120 V produz a mesma energia de aquecimento e iluminação em uma lâmpada que o 120 V de uma fonte de voltagem de CC. Pode ser mostrado que o valor efetivo ou rms de uma onda senoidal é:

Vrms = VM / √2 ≅ 0.707 VM
Esses valores podem ser calculados da mesma maneira para as voltagens e correntes.
O valor eficaz é muito importante na prática. A menos que indicado de outra forma, as tensões CA da rede elétrica (por exemplo, 110V ou 220V) são fornecidas em valores rms. A maioria dos medidores de CA são calibrados em rms e indicam o nível de rms.
Exemplo 1 Encontre o valor de pico da tensão senoidal em uma rede elétrica com valor 220 V rms.
VM = 220 / 0.707 = 311.17 V
Exemplo 2 Encontre o valor de pico da tensão senoidal em uma rede elétrica com valor 110 V rms.
VM = 110 / 0.707 = 155.58 V
Exemplo 3 Encontre a média (absoluta) da tensão senoidal se seu valor rms for 220 V.
Va = 0.637 * VM = 0.637 * 311.17 = 198.26 V
Exemplo 4 Encontre a média absoluta da tensão senoidal se seu valor eficaz for 110 V.
O pico da tensão do Exemplo 2 é 155.58 V e, portanto:
Va = 0.637 * VM = 0.637 * 155.58 = 99.13 V
Exemplo 5 Encontre a relação entre a média absoluta (Va) e valores rms (V) para a forma de onda sinusoidal.
V / Va = 0.707 / 0.637 = 1.11
Observe que você não pode adicionar valores médios em um circuito CA porque isso leva a resultados impróprios.
PHASORS
Como já vimos na seção anterior, é frequentemente necessário, em circuitos CA, adicionar tensões e correntes sinusoidais da mesma frequência. Embora seja possível adicionar os sinais numericamente usando TINA, ou empregando relações trigonométricas, é mais conveniente usar o chamado fasor método. Um fasor é um número complexo que representa a amplitude e a fase de um sinal senoidal. É importante notar que o fasor não representa a frequência, que deve ser a mesma para todos os fasores.
Um fasor pode ser tratado como um número complexo ou representado graficamente como uma seta plana no plano complexo. A representação gráfica é chamada de diagrama fasorial. Usando diagramas de fasores, você pode adicionar ou subtrair fasores em um plano complexo pela regra de triângulo ou paralelogramo.
Existem duas formas de números complexos: retangular e polar.
A representação retangular está na forma + jb, onde j = Ö-1 é a unidade imaginária.
A representação polar está na forma Aej j , onde A é o valor absoluto (amplitude) e f é o ângulo do fasor do eixo real positivo, no sentido anti-horário.
Nós vamos usar pino letras para quantidades complexas.
Agora vamos ver como derivar o fasor correspondente de uma função de tempo.
Primeiro, assuma que todas as tensões no circuito são expressas na forma de funções cosseno. (Todas as voltagens podem ser convertidas para essa forma). fasor correspondente à tensão de v (t) = VM cos ( w t+f) é: VM = VMe jf , que também é chamado de valor de pico complexo.
Por exemplo, considere a tensão: v (t) = 10 cos ( w t + 30°)
O fasor correspondente é: 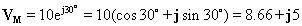
Podemos calcular a função tempo a partir de um fasor da mesma maneira. Primeiro escrevemos o fasor na forma polar, por exemplo VM = VMe jr e, em seguida, a função de tempo correspondente é
v (t) = VM (cos (wt+r).
Por exemplo, considere o fasor VM = 10 - j20 V
Trazendo-o para a forma polar:
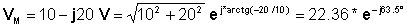
E, portanto, a função de tempo é: v (t) = 22.36 cos (wt - 63.5°V
Os fasores são freqüentemente usados para definir o valor efetivo ou eficaz complexo das tensões e correntes nos circuitos CA. Dado v (t) = VMcos (wt+r) = 10cos (wt + 30°)
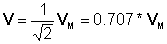
Numericamente:
v (t) = 10 * cos (wt-30°)
O valor efetivo complexo (rms): V = 0.707 * 10 * e- j30° = 7.07 e- j30° = 6.13 - j 3.535
Vice versa: se o valor efetivo complexo de uma tensão é:
V = - 10 + j 20 = 22.36 e j 116.5°
então o valor de pico complexo: 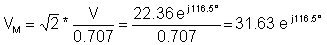
e a função do tempo: v (t) = 31.63 cos ( wt + 116.5° V
Uma justificativa curta das técnicas acima é a seguinte. Dada uma função de tempo
VM (cos ( w t+r), vamos definir o função de tempo complexo como:
v (t) = VM e jr e jwt = VMe jwt = VM (cos (r) + j pecado(r)) e jwt
onde VM =VM e j r t = VM (cos (r) + j pecado(r) é apenas o fasor introduzido acima.
Por exemplo, a função de tempo complexo de v (t) = 10 cos (wt + 30°)
v (t) = VMe jwt = 10 e j30 e jwt = 10e jwt (cos (30) + j sin (30)) = e jwt (8.66 +j5)
Introduzindo a função de tempo complexo, temos uma representação com uma parte real e uma parte imaginária. Podemos sempre recuperar a função real original do tempo tomando a parte real do nosso resultado: v (t) = Re {v(t)}
No entanto, a função de tempo complexo tem a grande vantagem de, uma vez que todas as funções complexas de tempo nos circuitos CA em consideração, têm o mesmojwt multiplicador, podemos fatorar isso e apenas trabalhar com os fasores. Além disso, na prática, não usamos o ejwt parte em tudo - apenas as transformações das funções de tempo para os fasores e vice-versa.
Para demonstrar a vantagem de usar fasores, vamos ver o exemplo a seguir.
Exemplo 6 Encontre a soma e a diferença das voltagens:
v1 = 100 cos (314 * t) e v2 = 50 cos (314 * t-45°)
Primeiro escreva os fasores de ambas as voltagens:
V1M = 100 V2M= 50 e - j 45° = 35.53 - j 35.35
Conseqüentemente:
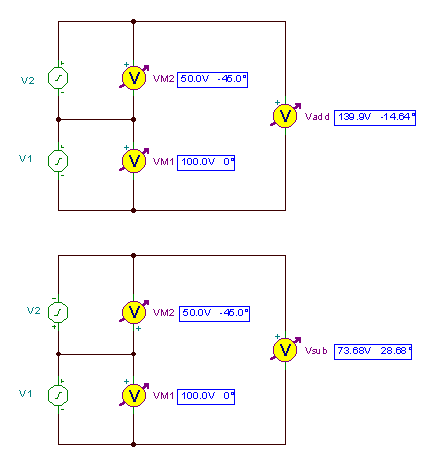
Vadicionar = V1M + V2M = 135.35 - j 35.35 = 139.89 e- j 14.63°
Vabaixo = V1M - V2M = 64.65 + j35.35 = 73.68 de j 28.67°
e depois as funções do tempo:
vadicionar(t) = 139.89 * cos (wt - 14.63°)
vabaixo(t) = 73.68 * cos (wt + 28.67°)
Como este exemplo simples mostra, o método dos fasores é uma ferramenta extremamente poderosa para resolver problemas de AC.
Vamos resolver o problema usando as ferramentas do intérprete da TINA.
{cálculo de v1 + v2}
v1: = 100
v2: = 50 * exp (-pi / 4 * j)
v2 = [35.3553-35.3553 * j]
v1add: = v1 + v2
v1add = [135.3553-35.3553 * j]
abs (v1add) = [139.8966]
radtodeg (arc (v1add)) = [- 14.6388]
{cálculo de v1-v2}
v1sub: = v1-v2
v1sub = [64.6447 + 35.3553 * j]
abs (v1sub) = [73.6813]
radtodeg (arc (v1sub)) = [28.6751]
#cálculo de v1+v2
importar matemática como m
importar cmath como c
v1=100
v2=50*c.exp(complexo(0,-c.pi/4))
imprimir(“v2=”,v2)
vadd=v1+v2
print(“vadd=”,vadd)
print(“abs(vadd)=”,abs(vadd))
print(“graus(arco(vadd))=”,m.graus(c.fase(vadd)))
#cálculo de v1-v2
vssub=v1-v2
imprimir(“vsub=”,vsub)
print(“abs(vsub)=”,abs(vsub))
print(“graus(arco(vsub))=”,m.graus(c.fase(vsub)))
Os resultados de amplitude e fase confirmam os cálculos das mãos.
Agora vamos verificar o resultado usando a análise AC da TINA.
Antes de executar a análise, vamos nos certificar de que Função base para AC ia definido para co-seno no Opções do Editor caixa de diálogo no menu Exibir / Opções. Vamos explicar o papel deste parâmetro em Exemplo 8.
Os circuitos e os resultados:
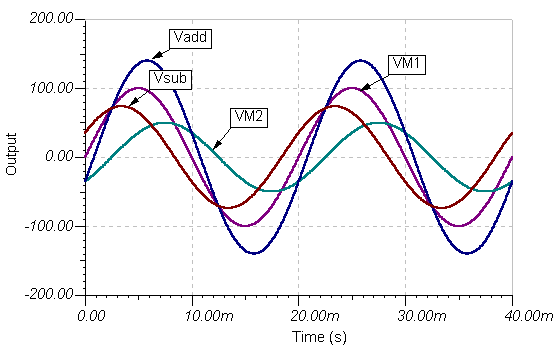
Mais uma vez o resultado é o mesmo. Aqui estão os gráficos de função de tempo:
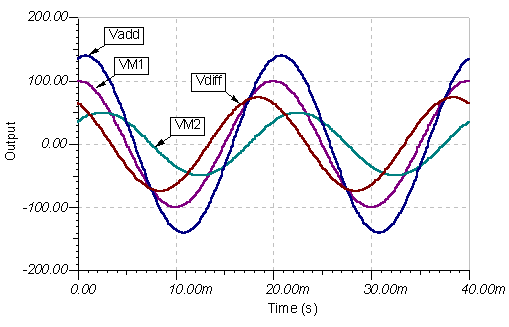
Exemplo 7 Encontre a soma e a diferença das voltagens:
v1 = 100 sin (314 * t) e v2 = 50 cos (314 * t-45°)
Este exemplo traz uma nova questão. Até agora, exigimos que todas as funções de tempo sejam dadas como funções cosseno. O que faremos com uma função de tempo dada como um seno? A solução é transformar a função seno em uma função cosseno. Usando a relação trigonométrica sin (x) = cos (x-p/ 2) = cos (x-90°), nosso exemplo pode ser reformulado da seguinte forma:
v1 = 100 cos (314t - 90°) e v2 = 50 cos (314 * t - 45°)
Agora os fasores das voltagens são:
V1M = 100 e - j 90° = -100 j V2M= 50 e - j 45° = 35.53 - j 35.35
Conseqüentemente:
V adicionar = V1M + V2M = 35.53 - j 135.35
V abaixo = V1M - V2M = - 35.53 - j 64.47
e depois as funções do tempo:
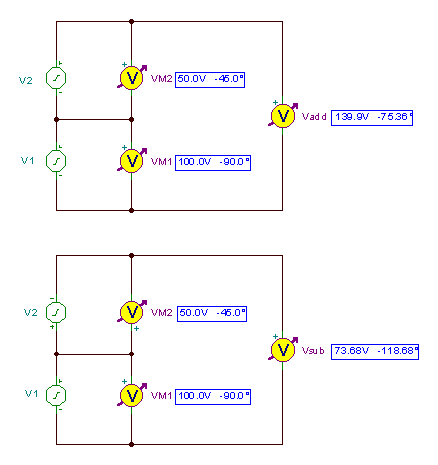
vadicionar(t) = 139.8966 cos (wt-75.36°)
vabaixo(t) = 73.68 cos (wt-118.68°)
Vamos resolver o problema usando as ferramentas do intérprete da TINA.
{cálculo de v1 + v2}
v1: = - 100 * j
v2: = 50 * exp (-pi / 4 * j)
v2 = [35.3553 - 35.3553 * j]
v1add: = v1 + v2
v1add = [35.3553-135.3553 * j]
abs (v1add) = [139.8966]
radtodeg (arc (v1add)) = [- 75.3612]
{cálculo de v1-v2}
v1sub: = v1-v2
v1sub = [- 35.3553 - 64.6447 * j]
abs (v1sub) = [73.6813]
radtodeg (arc (v1sub)) = [- 118.6751]
#cálculo de v1+v2
importar matemática como m
importar cmath como c
v1=100
v2=50*c.exp(complexo(0,-c.pi/4))
imprimir(“v2=”,v2)
vadd=v1+v2
print(“vadd=”,vadd)
print(“abs(vadd)=”,abs(vadd))
print(“graus(arco(vadd))=”,m.graus(c.fase(vadd)))
#cálculo de v1-v2
vssub=v1-v2
imprimir(“vsub=”,vsub)
print(“abs(vsub)=”,abs(vsub))
print(“graus(arco(vsub))=”,m.graus(c.fase(vsub)))
Vamos verificar o resultado com a análise AC da TINA
Exemplo 8
Encontre a soma e a diferença das voltagens:v1 = 100 sin (314 * t) e v2 = 50 sin (314 * t-45°)
Este exemplo traz mais um problema. E se todas as voltagens forem dadas como ondas senoidais e também desejamos ver o resultado como uma onda senoidal? Claro que poderíamos converter ambas as tensões em funções cosseno, calcular a resposta e então converter o resultado de volta em uma função seno - mas isso não é necessário. Podemos criar fasores a partir das ondas senoidais da mesma forma que fizemos a partir das ondas cossenoides e então simplesmente usar sua amplitude e fases como amplitude e fase das ondas senoidais no resultado.
Isso obviamente dará o mesmo resultado que transformar as ondas senoidais em ondas cosseno. Como pudemos ver no exemplo anterior, isso equivale a multiplicar por -j e, em seguida, usando o cos (x) = sin (x-90°) relação para transformá-lo de volta para uma onda senoidal. Isso é equivalente a multiplicar por j. Em outras palavras, desde -j × j = 1, poderíamos usar os fasores derivados diretamente das amplitudes e fases das ondas senoidais para representar a função e depois retornar diretamente a elas. Além disso, raciocinando da mesma maneira sobre as funções complexas do tempo, poderíamos considerar as ondas senoidais como as partes imaginárias das funções complexas do tempo e complementá-las com a função cosseno para criar a função complexa completa do tempo.
Vamos ver a solução para este exemplo usando as funções seno como base dos fasores (transformando o pecado ( w t) ao fasor da unidade real (1)).
V1M = 100 V2M= 50 e - j 45° = 35.53 - j 35.35
Conseqüentemente:
V adicionar = V1M + V2M = 135.53 - j 35.35
V abaixo = V1M - V2M = 64.47+ j 35.35
Note que os fasores são exatamente os mesmos que no Exemplo 6, mas não as funções de tempo:
v3(t) = 139.9sin (wt - 14.64°)
v4(t) = 73.68sin (wt + 28.68°)
Como você pode ver, é muito fácil obter o resultado usando funções seno, especialmente quando nossos dados iniciais são ondas senoidais. Muitos livros preferem usar a onda senoidal como a função base dos fasores. Na prática, você pode usar qualquer um dos métodos, mas não os confunda.
Quando você cria os fasores, é muito importante que todas as funções de tempo sejam primeiro convertidas para seno ou cosseno. Se você começou a partir de funções senoidais, suas soluções devem ser representadas com funções senoicas ao retornar de fasores para funções de tempo. O mesmo é verdadeiro se você começar com funções cosseno.
Vamos resolver o mesmo problema usando o modo interativo da TINA. Como queremos usar as funções senoicas como base para criar os fasores, certifique-se de que Função base para AC está definido para seu no Opções do Editor caixa de diálogo no menu Exibir / Opções.
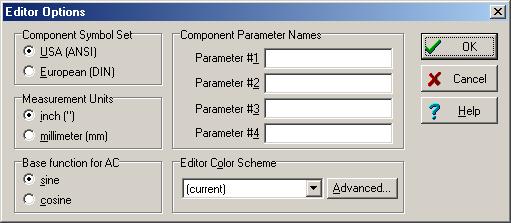

Os circuitos para fazer a soma e diferença das formas de onda e o resultado:
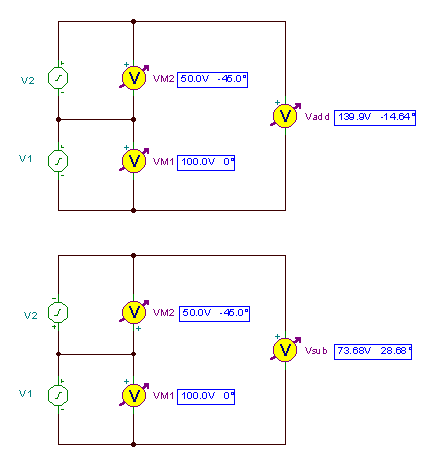
e o tempo funciona: