КОМПЛЕКС НӨМІРІ

TINACloud қолданбасын шақыру үшін төмендегі Мысал тізбектерін таңдаңыз немесе Интерактивті тұрақты режимін таңдаңыз, оларды Интернетте талдау.
Мысалдарды өңдеңіз немесе өзіңіздің сұлбаларыңызды жасау үшін TINACloud-ке төмен шығындарға қол жеткізіңіз

Альтернатива ағымының қағидаттары

Осы және келесі тарауларда өте маңызды тақырыпты ұсынамыз: айнымалы немесе ауыспалы ток. Айнымалы ток атауы өте дәл емес және әдетте синусоидальды кернеулер мен токтармен қамтитын тізбектерді қамтиды; алайда, айнымалы ток кез-келген ерікті ток толқындарын білдіре алады. Айнымалы ток кернеуінің маңыздылығы - бұл кернеудің мұндай түрі бүкіл әлем бойынша үйлер мен өнеркәсіптегі негізгі электр қуат көзі үшін пайдаланылады. Бұл сондай-ақ көптеген электроника, телекоммуникация және өнеркәсіптік қолдану үшін негіз болып табылады.

Синусоидальды толқындардың және олармен байланысты тізбектердің жұмыс істеуі үшін біз фазор әдісі деп аталатын қарапайым және талғампаз әдісті қолданамыз. Фазорлар синусоидальды шамаларды көрсету үшін өте ыңғайлы комплекстік сандардың қасиеттеріне негізделген. Осы тарауда күрделі сандар мен олардың қызметі туралы негізгі фактілерді жинақтаймыз. TINA-ның Ауызша аудармашысы күрделі сандармен есептеулерді жеңілдететінін көрсетеміз.

Кешенді нөмірлер екі бөліктен тұрады: a нақты бөлігі (x), бұл нақты сан және бұл деп аталады саналы бөлігі (y), көбейтілген нақты сан болып табылады 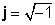, саналы бірлік. Кешеннің нөмірі zСондықтан, келесідей сипаттауға болады:

z = x + jy

қайда .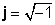

Кешенді нөмірлердің мысалдары:

z 1 = 1 + j

z 2 = 4-2 j

z 3 = 3- 5j

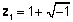
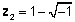
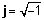
Күрделі сандар ең алдымен XVII ғасырда полиномдардың тамырларын білдіру үшін енгізілген, оларды нақты сандармен көрсету мүмкін емес. Мысалы, х теңдеуінің түбірлері2 + 2x + 2 = 0 ретінде сипаттауға болады және немесе белгілерді қолданыңыз , z1= 1 + j және z2= 1- j. Өрнектердің қасиеттерін зерттеу үшін жаңа белгіні қолдана отырып, математиктер теоремаларды дәлелдей алды және сол кезге дейін қиын болған, мүмкін болмаса шешуге болатын мәселелерді шеше алды. Бұл қазіргі уақытта математика мен техникада кеңінен қолданылатын күрделі алгебра мен күрделі функцияларды жасауға әкелді.

Күрделі сандардың геометриялық көрінісі

Тікбұрышты пішін

Күрделі санды әрқашан оның нақты және күрделі бөліктеріне бөлуге болатындықтан, біз комплексті санды екі өлшемді жазықтықта нүкте ретінде ұсына аламыз. Күрделі санның нақты бөлігі - нүктенің нақты оське проекциясы, ал санның қиял бөлігі - қиялдың осіне проекциясы. Күрделі сан нақты және қиялдың бөліктерінің қосындысы ретінде берілгенде, біз оны деп айтамыз тікбұрышты or алгебралық нысан.


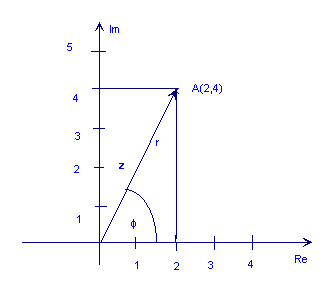
Төмендегі суретте күрделі сан көрсетіледі z = 2 + 4j

Полярлық және экспоненттік формасы

Жоғарыдағы суреттен көріп отырғаныңыздай, А нүктесі де жебенің ұзындығымен көрсетілуі мүмкін, r (сонымен қатар абсолютті мән, үлкендік немесе амплитуда деп аталады) және оның бұрышы (немесе фазасы), φ сағат тіліне қарсы бағытта оң горизонталь осіне қатысты. Бұл полярлық күрделі санның түрі. Ол r ∠ деп белгіленеді φ.

Келесі қадам өте маңызды. Полярлы түрде күрделі сан болуы да мүмкін экспоненталық нысаны:

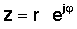
Бұл қарапайым өрнектің ерекшелігі, ол кәдімгі нақты санның орнына экспонентте қиялдық нөмірге ие. Бұл күрделі экспоненциалды әрекет нақты экспоненциалды экспоненциалды функциядан өзгеше болады. Кезінде ex x> 0 ұлғайту үшін шамасы бойынша тез өседі, ал x <0 үшін азаяды, функциясы 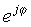шамасы бірдей (z = 1) кез келген φ үшін. Оның күрделі мәні бірлік шеңберде орналасқан.

Эйлер формуласы күрделі сандардың тікбұрышты, полярлы және экспоненциалды формалары арасында біріктіруші байланыс ұсынады:

z = x + jy = re jφ = r (cos φ + j күнә φ )

қайда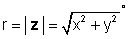

және φ = тан-1 (Y / x).

Жоғарыда келтірілген мысал үшін, z = 2 + 4j:

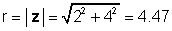
φ = тан-1 (4 / 2) = 63.4 °

сондықтан .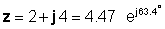

Немесе керісінше:

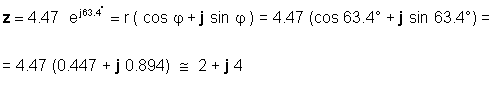
Өтінішке байланысты екі форманы да қолданған жөн. Мысалы, сандар тікбұрышты формада болған кезде қосу немесе азайту оңай, ал көбейту және бөлу экспоненциалды формада болған кезде жасау оңайырақ.

Күрделі сандармен операциялар

Күрделі сандармен жасалатын операциялар нақты сандарға ұқсас. Төменде ережелер мен кейбір жаңа анықтамалар келтірілген.

J

Операциялар j жай ғана мнимый бірліктің анықтамасынан кейін,

Жылдам әрі нақты жұмыс істеу үшін осы ережелерді есте сақтау қажет:

j 2 = -1

j 3 =-j

j 4 =1

1/j = -j

Дәлелдеу:

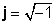
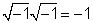
j2 = -1 анықтамасынан өте алады , өйткені

1 /j, біз 1 /jby j / j = 1 және алыңыз j/ (jj) = j / (- 1) = -j.

Кешенді түйіспе

Күрделі санның күрделі түйісуін оңай алуға болады және өте маңызды. Күрделі санның күрделі түйісуін тікбұрышты түрде алу үшін, мнимой бөліктің белгісін өзгертіңіз. Экспоненциалды пішіндегі сан үшін мұны абсолюттік мәнін бірдей сақтай отырып, күрделі санның бұрышын өзгертіңіз.

Күрделі санның кешенді түйісуі z жиі көрсетіледі z*.

Кешенді нөмірді ескере отырып z= a + jb, оның күрделі конъюгаты z*= a- jb.

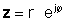
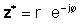
If z экспоненталық түрде беріледі, , оның күрделі ұштасуы

Жоғарыда келтірілген анықтамаларды пайдалана отырып, күрделі санын күрделі коньюгатпен көбейтіп, күрделі санның абсолютті мәнінің квадратын береді:

zz* = r2 = a2 + b2

Сондай-ақ, кез-келген күрделі санды және оның түйісуін қосу немесе алып тастау арқылы келесі қатынастарды аламыз:

z + z * = 2a

сондықтан

Re (z) = a = ( z + z * ) / 2

Сол сияқты:

z - z * =j2b

сондықтан

Im (z) = b = ( z -z * ) / 2j

Дәлелдеу:

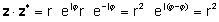
немесе нақты және ойланатын бөліктерді көбейтуге және пайдалану j2= -1

zz* = (a + jb) (а - jб) = а2+a jб - а jb - jbjb = a2j2 = a2 + b2

z + z* = a + jb + a - jb = 2a

z - z*= a + jb - a + jb =j2b

Сандық мысалдар:

Төрт бұрышты түрінде:

z = 3 + j4

z* = 3- j4

zz * = 9 + 16 = 25

Полярлы түрде

z = 5 ∠ 53.13 °

z * = 5 ∠- 53.13 °

Экспоненттік түрде:

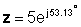
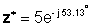
Қосу және алу

Күрделі сандарды қосу және азайту оңай - тек нақты және қиял бөліктерін бөлек қосу керек. Мысалы, егер

z1 = 3 - 4j және z2 = 2 + 3j

содан кейін

z1 + z2 = 3 - 4j + 2 + 3j = 3 + 2 - 4j + 3j = 5 - j

z1 - z2 = 3 - 4j - 2 - 3j = 3 - 2 - 4j - 3j = 1 - j7

Біз бұл операциялар үшін тікбұрышты форманы пайдалануымыз керек екені анық. Егер сандар экспоненциалды немесе полярлық түрінде берілсе, біз оларды бұрын Эйлер формуласын қолдана отырып тік төртбұрыш түріне айналдыруымыз керек.

Көбейту

Күрделі сандарды көбейтудің екі әдісі бар -

Тіктөртбұрыш түрінде берілген күрделі сандарды көбейту

Операцияны орындау үшін бір санның нақты және қиял бөліктерін басқа санның нақты және қиял бөліктеріне кезекпен көбейтіп, сәйкестендіруді қолданыңыз j2 = -1.

z1z2 = (а1 + jb1) (а2 + jb2) = a1 a2 + jb1a2+ jb2a1 - b1b2 = a1 a2- b1b2 + j(b1a2+ jb2a1)

Күрделі сандар сандық түрде берілсе, жоғарыдағы формуланы пайдаланудың қажеті жоқ. Мысалы, рұқсат беріңіз

z1 = 3 - 4j және z2 = 2 + 3j

Тікелей көбейту арқылы компоненттер:

z1z2 = (3 - 4j) (2 + 3j) = 6- 8j +9j + 12 = 18 + j

немесе формуланы пайдалана отырып: z1z2 = a1 a2- b1b2 + j(b1a2+ b2a1)

z1z2 = 6 + 12 + j (-8 + 9) = 18 + j

Егер формуланы тікелей компоненттерді көбейтуге қарағанда пайдалансаңыз, сіз қате жасай аласыз деп ойлаймыз.

{TINA аудармашысының шешімі}
z1: = 3-4 * j
z2: = 2 + 3 * j
z1 * z2 = [18 + 1 * j]
#Python шешімі:
математиканы m ретінде импорттау
c ретінде импорт смат

z1=күрделі('3-4j')
z2=күрделі('2+3j')
басып шығару(“z1*z2=”,z1*z2)

Полярлық немесе экспоненциалды түрде берілген күрделі сандарды көбейту

Бұл операцияны орындау үшін абсолютті мәндерді көбейтіп, екі күрделі санның бұрыштарын қосыңыз. Келіңіздер:

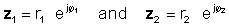
Содан кейін экспоненциалды функциялардың көбейту ережесін қолданыңыз:

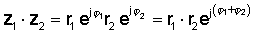
немесе полярлы түрде

z1 z2 = r1 r2 ∠ φ1 + φ2

Ескерту: есептелгенде біз бұл ережені қолдандық zz *жоғарыда. Конъюгаттың бұрышы бастапқы бұрыштың қарама-қарсы белгісіне ие болғандықтан, меншікті конъюгаты көбейтілген күрделі сан әрқашан нақты сан болып табылады; оның абсолютті шамасының квадраты: zz * = r2

Мысалы:

z1 = 5 ∠ 30 ° және z2 = 4 ∠ -60 °

содан кейін

z1z2 = 20 ∠ -30 °

немесе экспоненталық пішінде

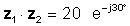
Сандар полярлы немесе экспоненциалды түрде болғанда, көбейту оңайырақ.

Алайда, егер күрделі сандар тікбұрышты түрінде берілсе, көбейтуді тікелей жоғарыда көрсетілгендей орындауды қарастыру керек, өйткені сандарды көбейтпес бұрын полярлық пішінге түрлендірсеңіз қосымша қадамдар болады. Тағы бір назар аударатын фактор - жауаптардың тікбұрышты немесе полярлы / экспоненциалды формада болуын қалайсыз ба. Мысалы, егер екі сан тікбұрышты пішінде болса, бірақ олардың полярлық түрінде болғанын қаласаңыз, оларды бірден түрлендіріп, содан кейін көбейту керек.

бөлу

Күрделі сандарды бөлудің екі әдісі бар -

Күрделі сандарды бөлу тік бұрышты түрінде берілген

Операцияны орындау үшін алымды және бөлгішті шартты белгінің қосындысына көбейтіңіз. Нөмір нақты санға айналады және бөлу екі күрделі санның көбейтуіне және нақты санға бөлудің, абсолютті шаманың квадратына көбейтуге азаяды.


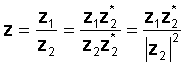
Мысалы:

z1 = 3 - 4j және z2 = 2 + 3j

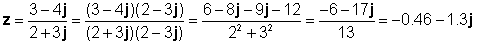
Бұл нәтижені TINA аудармашымен тексерейік:

{TINA аудармашысының шешімі}
z1: = 3-4 * j
z2: = 2 + 3 * j
z1 / z2 = [- 461.5385m-1.3077 * j]
#Python шешімі:
математиканы m ретінде импорттау
c ретінде импорт смат

z1=күрделі('3-4j')
z2=күрделі('2+3j')
басып шығару(“z1/z2=”,z1/z2)

Полярлық немесе экспоненциалды түрде берілген кешенді нөмірлерді бөлу

Операцияны орындау үшін абсолюттік мәндерді (шамаларды) бөліп, матрицаның бұрышын нумератор бұрышынан шығарыңыз. Келіңіздер:

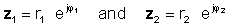
содан кейін экспоненциалды функцияларды бөлу ережесін қолданыңыз

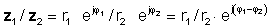
немесе полярлы түрде

z 1 / z2 = r1 / r2 ∠ φ 1- φ 2

Мысалы:

z 1 = 5 ∠ 30 ° және z 2 = 2 ∠ -60 °

содан кейін

z 1 / z2 = 2.5 ∠ 90 °

немесе экспоненциалды және тікбұрышты нысандарда

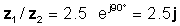
Бұл нәтижені TINA аудармашымен тексерейік:

{TINA аудармашысының шешімі}
z1: = 5 * exp (j * degtorad (30))
z2: = 2 * exp (j * degtorad (-60))
z1 / z2 = [0 + 2.5 * j]
#Python шешімі:
математиканы m ретінде импорттау
c ретінде импорт смат

z1=5*(c.exp(күрделі(0,м.радиан(30))))
z2=2*(c.exp(күрделі(0,м.радиан(-60))))
басып шығару(“z1/z2=”,z1/z2)

Сандар полярлы немесе экспоненциалды формада болған кезде бөлу оңайырақ болады.

Алайда, егер күрделі сандар тіктөртбұрыш түрінде берілсе, бөлуді жоғарыда көрсетілгендей күрделі біріктіру әдісін қолдана отырып жасауды қарастыру керек, өйткені сандарды бөлудің алдында полярлық пішінге түрлендірсеңіз қосымша қадамдар болады. Тағы бір назар аударатын фактор - жауаптардың тікбұрышты немесе полярлы / экспоненциалды формада болуын қалайсыз ба. Мысалы, егер екі сан тіктөртбұрыш түрінде болса, бірақ олардың полярлық түрінде берілгенін қалайсыз, оларды бірден түрлендіріп, содан кейін бөлу керек.

Енді күрделі сандарды қолданудың сандық проблемаларымен түсіндірейік. Әдеттегідей, TINA компаниясының аудармашысы арқылы шешімдерімізді тексереміз. Аудармашы радиандықтармен жұмыс істейді, бірақ радианның градусқа немесе керісінше түрлендіру үшін стандартты функциялары бар.

Мысал 1 Полярлық көріністі табу:

z = 12 - j 48

немесе 49.48 ∠ - 75.96 °

{TINA аудармашысының шешімі}
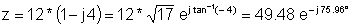
z: = 12-j * 48;
abs (z) = [49.4773]
арка (z) = [- 1.3258]
radtodeg (arc (z)) = [- 75.9638]
#Python шешімі:
математиканы m ретінде импорттау
c ретінде импорт смат

z=12-комплекс(48j)
басып шығару(“abs(z)=”,abs(z))
басып шығару(“arc(z)=”,c.phase(z))
print(“degrees(arc(z))=”,m.degrees(c.phase(z)))

Мысал 2 Тіктөртбұрышты ұсынуды табыңыз:

z = 25 e j 125 °

{TINA аудармашысының шешімі}
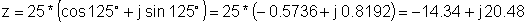
z: = 25 * exp (j * (degtorad (125)));
z = [- 14.3394 + 20.4788 * j]
Re (z) = [- 14.3394]
Im (z) = [20.4788]
#Python шешімі:
математиканы m ретінде импорттау
c ретінде импорт смат

z=25*c.exp(күрделі(0,м.радиан(125)))
басып шығару(“z=”,z)
print(“real(z)=”,z.real)
басып шығару(“imag(z)=”,z.imag)

Мысал 3 Келесі кешенді нөмірлердің полярлық көрінісін табыңыз:

z 1 = 12 + j 48 z2 = 12 - j48 z3= -12 + j 48 z4= -12 - j 48

Барлық төрт санның абсолютті мәні бірдей, өйткені абсолютті мән белгілерге тәуелсіз. Тек бұрыштары әртүрлі.

{TINA аудармашысының шешімі}
z1: = 12 + j * 48;
abs (z1) = [49.4773]
арка (z1) = [1.3258]
radtodeg (арка (z1)) = [75.9638]

z2: = 12-j * 48;
abs (z2) = [49.4773]
арка (z2) = [- 1.3258]
radtodeg (арка (z2)) = [- 75.9638]

z3: = - 12 + j * 48;
abs (z3) = [49.4773]
арка (z3) = [1.8158]
radtodeg (арка (z3)) = [104.0362]

z4: = - 12-j * 48:
abs (z4) = [49.4773]
арка (z4) = [- 1.8158]
radtodeg (арка (z4)) = [- 104.0362]
#Python шешімі:
математиканы m ретінде импорттау
c ретінде импорт смат

z1=күрделі('12+48j')
басып шығару(“abs(z1)=”,abs(z1))
print(“arc(z1)=”,c.phase(z1))
print(“degrees(arc(z1))=”,m.degrees(c.phase(z1)))

z2=күрделі('12-48j')
басып шығару(“abs(z2)=”,abs(z2))
print(“arc(z2)=”,c.phase(z2))
print(“degrees(arc(z2))=”,m.degrees(c.phase(z2)))

z3=күрделі('-12+48j')
басып шығару(“abs(z3)=”,abs(z3))
print(“arc(z3)=”,c.phase(z3))
print(“degrees(arc(z3))=”,m.degrees(c.phase(z3)))

z4=күрделі('-12-48j')
басып шығару(“abs(z4)=”,abs(z4))
print(“arc(z4)=”,c.phase(z4))
print(“degrees(arc(z4))=”,m.degrees(c.phase(z4)))

TINA доғасы () функциясы кез-келген күрделі санның бұрышын анықтайды, оны автоматты түрде оны төрт квадранттың біріне дұрыс орналастырады.

Дегенмен, балды қолданғанда абай болыңыз-1 бұрышты табу функциясы, өйткені ол тек бірінші және төртінші ширектерде бұралу бұрыштарымен шектеледі (–90 °)φ<90 °).

содан бері z1 координат жүйесінің алғашқы квадрантында орналасқан, есептеу:

α 1 = тан-1(48 / 12) = тан-1(4) = 75.96 °

содан бері z4 координат жүйесінің үшінші квадрантында орналасқан-1бұрышты дұрыс қайтармайды. Бұрышты есептеу:

α 4 = 180 ° + 75.96 ° = 255.96 ° немесе -360 ° + 255.96 ° = - 104.04 °, бұл TINA есептегенмен бірдей.

z2 координат жүйесінің төртінші квадрантында орналасқан Бұрыштық есептеу:

α 2 = тан-1(-48 / 12) = тан-1(-4) = -75.96 °

z3, алайда, координат жүйесіндегі 2nd квадрантында орналасқан, сондықтан да-1 бұрышты дұрыс қайтармайды. Бұрышты есептеу:

α 3 = 180 ° -75.96 ° = 104.04 °.

Мысал 4 Бізде екі күрделі сан бар: z1= 4 - j 6 және z2 = 5 ej45 ° .

табу z3 = z1 + z2; z4 = z1 - z2; z5 = z1 * z2; z6 = z1 / z2

Алдымен TINA-ның аудармашының көмегімен мәселені шешеміз

{TINA аудармашысының шешімі}
z1: = 4-j * 6;
z2: = 5 * exp (j * degtorad (45));
z3: = z1 + z2;
z3 = [7.5355-2.4645 * j]
z4: = z1-z2;
z4 = [464.4661m-9.5355 * j]
z5: = z1 * z2;
z5 = [35.3553-7.0711 * j]
z6: = z1 / z2;
z6 = [- 282.8427m-1.4142 * j]

TINA әртүрлі формаларда берілген екі күрделі сандарды қалай оңай жұмыс істейтініне назар аударыңыз.

Шешімі аудармашысыз қиынырақ. Көбейту мен бөлудің әртүрлі әдістерін салыстыру үшін алдымен полярлық форманы анықтаймыз z1 және тікбұрышты нысаны z2 .

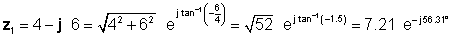
Әрі қарай, алдымен ең оңай формаларды қолдана отырып төрт шешім табамыз: қосу және алу үшін тікбұрышты, көбейту мен бөлуге арналған экспоненциал:

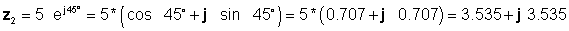
z 3 = z1 + z2 = 4 - j 6 + 3.535 + j 3.535 = 7.535 - j2.465

z 4 = z1 - z2 = 4 - j 6 - 3.535 - j 3.535 = 0.465 - j9.535

z 5 = z1 * z2 = 7.21 * 5 * ej(-56.31 ° + 45 °) = 36.05 e -j11.31 ° = 36.03 * (cos (-11.31 °) +)j* sin (-11.31 °))

z 5 = 35.33 - j 7.07

z 6 = z1/z2= (7.21 / 5) * e j (-56.31 ° -45 °) = 1.442 e - j 101.31 ° = 1.442 (cos (-101.31 °) +)j* sin (-101.31 °))

z 6 = -0.2828 - j 1.414

TINA аудармашымен алынған нәтижелермен келіседі.

Көтеріп алу төртбұрышты түрінде жүзеге асырылады:

z 5 =z1*z2 = (4-j6) * 3.535 * (1 +j) = 7.07 * (2-j3) * (1 +j) = 7.07 * (2-j3+j2 + 3) = 7.07 * (5-j) = 35.35-j7.07

Ақыр соңында бөлу тікбұрышты түрде жүзеге асырылады:

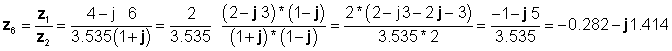
олар алдыңғы нәтижелермен келіседі.

Альтернатива ағымының қағидаттары

en English
en Englishde Germanfr Frenches Spanishpt Portugueseru Russianzh-CN Chinese (Simplified)zh-TW Chinese (Traditional)ja Japaneseko Koreanhu Hungarian