 Кликнете или допрете ги Примерните кола подолу за да го повикате TINACloud и да го одберете интерактивниот DC режим за да ги анализирате Online.
Кликнете или допрете ги Примерните кола подолу за да го повикате TINACloud и да го одберете интерактивниот DC режим за да ги анализирате Online. Добијте низок пристап до TINACloud за да ги уредите примерите или да креирате сопствени кола
Во ова и во следните поглавја, ќе претставиме многу важна тема: наизменична струја или наизменична струја. Името на наизменична струја не е многу прецизно и нормално ги опфаќа кола со синусоидни напони и струи; сепак, наизменичната струја, исто така, може да значи и било произволни бранови. Важноста на AC напонот е тоа што овој вид на напон се користи за главниот извор на електрична енергија во домовите и индустријата ширум светот. Тоа е исто така основа за многу електронски, телекомуникациски и индустриски апликации.
За да се справи со sinusoidal бранови форми и кола поврзани со нив, ние ќе го користиме едноставен и елегантен метод наречен метод на phazors. Phazors се базираат на својствата на комплексните броеви, кои се идеални за претставување на синусоидални количини. Во ова поглавје ќе ги сумираме главните факти за комплексните броеви и нивните операции. Ние исто така ќе покажеме како преведувачот на TINA олеснува да се прават пресметки со сложени броеви.
Комплексните броеви се состојат од два дела, а вистински дел (x), што е вистински број, и т.н. имагинарен дел (y), што е вистински број помножен со 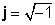
z = x + jy
каде 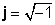
Примери на комплексни броеви:
z 1 = 1 + j
z 2 = 4-2 j
z 3 = 3- 5j
Комплексните броеви првично беа воведени во седумнаесеттиот век за да ги претставуваат корените на полиноми кои не може да бидат претставени само со вистински броеви. На пример, корените на равенката x2 + 2x + 2 = 0 може да се опише само како 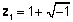
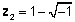
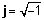
Геометриска застапеност на сложени броеви
Правоаголна форма
Бидејќи комплексен број секогаш може да се одвои во неговите реални и комплексни делови, можеме да претставуваме комплексен број како точка на дводимензионална рамнина. Вистинскиот дел од сложениот број е проекција на точката кон реалната оска, а имагинарен дел од бројот е проекција кон имагинарната оска. Кога сложен број е претставен како збир на реални и имагинарни делови, ние велиме дека е во правоаголна or алгебарска форма.
Следнава слика го покажува комплексниот број z = 2 + 4j
Поларна и експоненцијална форма
Како што можете да видите од сликата погоре, точката А исто така може да биде претставена со должината на стрелата, r (исто така се нарекува апсолутна вредност, големина или амплитуда) и нејзиниот агол (или фаза), φ релативна во насока спротивно од стрелките на часовникот кон позитивната хоризонтална оска. Ова е поларна форма на комплексен број. Се означува како r φ.
Следниот чекор е многу важен. Комплетен број во поларна форма, исто така, може да биде напишан во експоненцијална форма:
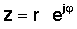
Овој едноставен израз е карактеристичен по тоа што има имагинарен број во експонентот наместо вообичаениот реален број. Овој комплекс експоненцијален се однесува многу поинаку од експоненцијалната функција со вистински аргумент. Додека еx рапидно расте со големина за зголемување x> 0 и се намалува за x <0, функцијата 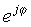
Формулата на Ојлер обезбедува обединувачка врска меѓу правоаголните, поларните и експоненцијалните форми на сложени броеви:
z = x + jy = повторно jφ = r (cos φ + j без φ )
каде 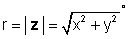
φ = тен-1 (y / x).
За нашиот пример погоре, z = 2 + 4j:
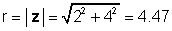
φ = тен-1 (4 / 2) = 63.4 °
затоа 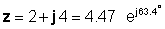
Или обратно:
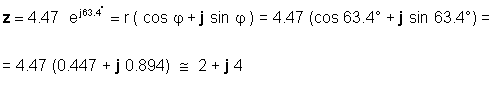
Dependingе треба да бидете вешти во користењето на двете форми, во зависност од апликацијата. На пример, додавање или одземање очигледно е полесно да се направи кога броевите се во правоаголна форма, додека множењето и делењето се полесно да се прават кога броевите се во експоненцијална форма.
Операции со комплексни броеви
Операциите што можат да се извршат со сложени броеви се слични на оние за реални броеви. Правилата и некои нови дефиниции се сумирани подолу.
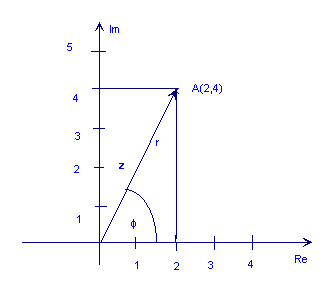
Операции со j
Операциите со j едноставно следат од дефиницијата на имагинарната единица,


За да можете да работите брзо и прецизно, треба да ги запомните овие правила:
j 2 = -1
j 3 =-j
j 4 =1
1/j = -j
j2 = -1 едноставно следи од дефиницијата на 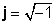
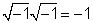
За 1 /j, ние множиме 1 /jby j / j = 1 и да се добие j/ (jj) = j / (- 1) = -j.
Комплексен конјугат
Сложениот конјугат на комплексен број лесно се изведува и е многу важен. За да се добие комплексниот конјугат на комплексен број во правоаголна форма, едноставно го менува знакот на имагинарниот дел. За да го стори тоа за број во експоненцијална форма, сменете го знакот на аголот на комплексниот број, истовремено држејќи ја неговата апсолутна вредност иста.
Комплексниот конјугат на комплексен број z често се означува со z*.
Со оглед на комплексниот број z= a + jб, неговиот комплексен конјугат е z*= a- jb.
If z е дадена во експоненцијална форма, 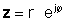
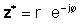
Користејќи ги горенаведените дефиниции, лесно е да се види дека комплексниот број множи со комплексниот конјугат, дава квадрат на апсолутната вредност на комплексниот број:
zz* = р2 = a2 + b2
Исто така, со додавање или одземање на кој било комплексен број и неговиот конјугиран, ги добиваме следниве релации:
z + z * = 2a
затоа
Re (z) = a = ( z + z * ) / 2
Слично на тоа:
z - z * =j2b
затоа
Јас сум(z) = b = ( z -z * ) / 2j
Доказ:
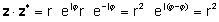
или множење на вистински и имагинарни делови и користење j2= -1
zz* = (a + jб) (а - jб) = а2+a jб - а jb - jbjb = a2j2 = a2 + b2
z + z* = a + jb + a - jb = 2a
з - з*= a + jb - a + jb =j2b
Нумерички примери:
Во правоаголна форма:
z = 3 + j4
z* = 3- j4
zz * = 9 + 16 = 25
Во поларна форма
z = 5 ∠ 53.13 °
z * = 5 ∠- 53.13 °
Во експоненцијална форма:
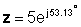
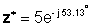
Додавање и одземање
Додавањето и одземањето на комплексни броеви е едноставна - треба да ги додадеме само реалните и имагинарните делови одделно. На пример, ако
z1 = 3 - 4j z2 = 2 + 3j
потоа
z1 + z2 = 3 - 4j + 2 + 3j = 3 + 2 - 4j + 3j = 5 - j
z1 - z2 = 3 - 4j - 2 - 3j = 3 - 2 - 4j - 3j = 1 - j7
Очигледно, треба да користиме правоаголна форма за овие операции. Ако броевите се дадени во експоненцијална или поларна форма, ние треба прво да ги претвориме во правоаголна форма користејќи ја формулата Ојлер, како што е дадено порано.
Множење
Постојат два методи за множење на сложени броеви–
Множење на комплексните броеви дадени во правоаголна форма
За извршување на операцијата, едноставно помножете ги реалните и имагинарните делови од еден број за возврат со реалните и имагинарните делови од другиот број и користете го идентитетот j2 = -1.
z1z2 = (а1 + jb1) (а2 + jb2) = a1 a2 + jb1a2+ jb2a1 - б1b2 = a1 a2- б1b2 + j(b1a2+ jb2a1)
Кога комплексните броеви се дадени нумеричко, не е неопходно да се користи формулата погоре. На пример, нека
z1 = 3 - 4j z2 = 2 + 3j
Со директно множење на компонентите:
z1z2 = (3 - 4j) (2 + 3j) = 6-8j +9j + 12 = 18 + j
или со користење на формулата: z1z2 = a1 a2- б1b2 + j(b1a2+ б2a1)
z1z2 = 6 + 12 + j (-8 + 9) = 18 + j
Мислиме дека е поголема веројатноста да направите грешка ако ја користите формулата отколку ако директно ги множествувате компонентите.
z1: = 3-4 * j
z2: = 2 + 3 * j
z1 * z2 = [18 + 1 * j]
увезете математика како m
увезете cmath како в
z1=комплекс ('3-4j')
z2=комплекс ('2+3j')
печатење (“z1*z2=”,z1*z2)
Множење на комплексните броеви дадени во поларна или експоненцијална форма
За да ја извршите оваа операција, помножете ги апсолутните вредности и додајте ги аглите на двата комплексни броеви. Дозволете:
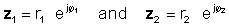
Потоа користејќи го правилото за множење на експоненцијални функции:
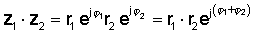
или во поларна форма
z1 z2 = р1 r2 Φ1 + φ2
Забелешка: Ние веќе го користевме ова правило кога пресметувавме zz *погоре Бидејќи аголот на конјугатот има спротивен знак на оригиналниот агол, сложениот број помножен со сопствениот коњугат е секогаш вистински број; имено, плоштадот на нејзината апсолутна вредност: zz * = р2
На пример, дозволете:
z1 = 5 ∠ 30 ° и z2 = 4 ∠ -60 °
потоа
z1z2 = 20 ∠ -30 °
или во експоненцијална форма
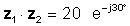
Множењето е очигледно поедноставно кога броевите се во поларна или експоненцијална форма.
Меѓутоа, ако сложените броеви се дадени во правоаголна форма, треба да размислите да ја извршите множењето директно како што е прикажано погоре, бидејќи има дополнителни чекори ако ги претворите броевите во поларна форма пред да ги умножите. Друг фактор што треба да се разгледа е дали сакате одговорите да бидат во правоаголна форма или во поларна / експоненцијална форма. На пример, ако двата броја се во правоаголна форма, но сакате нивниот производ во поларна форма, има смисла да ги конвертирате веднаш, а потоа да ги размножуваат.
Поделба
Постојат два методи за поделба на сложените броеви–
Поделба на комплексни броеви дадени во правоаголна форма
За извршување на операцијата, помножете ги бројачот и именителот со коњугатот на именителот. Деноминаторот станува вистински број и поделбата се сведува на множење на два сложени броја и поделба по реален број, квадрат на апсолутна вредност на именител.
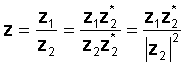
На пример, дозволете:
z1 = 3 - 4j z2 = 2 + 3j
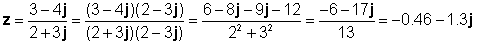
Да го провериме овој резултат со преведувачот на TINA:
z1: = 3-4 * j
z2: = 2 + 3 * j
z1 / z2 = [- 461.5385m-1.3077 * j]
увезете математика како m
увезете cmath како в
z1=комплекс ('3-4j')
z2=комплекс ('2+3j')
печатење („z1/z2 =“, z1/z2)
Поделба на комплексни броеви дадени во поларна или експоненцијална форма
За извршување на операцијата, подели ги апсолутните вредности (величини) и го одземе аголот на именителот од аголот на броителот. Дозволете:
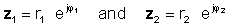
потоа со користење на правило за поделба на експоненцијални функции
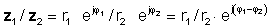
или во поларна форма
z 1 / z2 = р1 / r2 ∠ φ 1- φ 2
На пример, дозволете:
z 1 = 5 ∠ 30 ° и z 2 = 2 ∠ -60 °
потоа
z 1 / z2 = 2.5 ∠ 90 °
или во експоненцијални и правоаголни форми
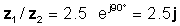
Да го провериме овој резултат со преведувачот на TINA:
z1: = 5 * exp (j * degtorad (30))
z2: = 2 * exp (j * degtorad (-60))
z1 / z2 = [0 + 2.5 * j]
увезете математика како m
увезете cmath како в
z1=5*(c.exp(комплекс(0,m.радијани(30))))
z2=2*(c.exp(комплекс(0,m.радијани(-60))))
печатење („z1/z2 =“, z1/z2)
Поделбата е очигледно поедноставна кога броевите се во поларна или експоненцијална форма.
Меѓутоа, ако сложените броеви се дадени во правоаголна форма, треба да размислите да ја извршите поделбата директно користејќи го комплексот метод на конјугат како што е прикажано погоре, бидејќи има дополнителни чекори ако ги претворите броевите во поларна форма пред да ги поделите. Друг фактор што треба да се разгледа е дали сакате одговорите да бидат во правоаголна форма или во поларна / експоненцијална форма. На пример, ако двата броја се во правоаголна форма, но вие би сакале нивниот количник во поларна форма, има смисла да ги конвертирате веднаш, а потоа да ги поделите.
Сега да ја илустрираме употребата на комплексни броеви со повеќе нумерички проблеми. Како и обично, ние ќе ги провериме нашите решенија користејќи преведувач на TINA. Преведувачот работи со радијани, но има стандардни функции за претворање на радијани во степени или обратно.
Пример 1 Најдете поларна репрезентација:
z = 12 - j 48
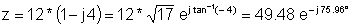
z: = 12-j * 48;
abs (z) = [49.4773]
arc (z) = [- 1.3258]
radtodeg (arc (z)) = [- 75.9638]
увезете математика како m
увезете cmath како в
z=12-комплекс (48j)
печатење (“abs(z)=”,abs(z))
печатење („лак(z)=“, в.фаза(z))
печатење (“степени(лак(z))=”,м.степени(в.фаза(z)))
Пример 2 Најдете правоаголна застапеност:
z = 25 e j 125 °
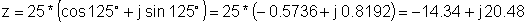
z: = 25 * exp (j * (degtorad (125)));
z = [- 14.3394 + 20.4788 * j]
Re (z) = [- 14.3394]
Im (z) = [20.4788]
увезете математика како m
увезете cmath како в
z=25*c.exp(комплекс(0,m.радијани(125)))
печатење (“z=”, z)
печатење („реално(з)=“, з.реално)
печатење („имаг(з)=“, з.имаг)
Пример 3 Пронајдете ја поларната репрезентација на следниве комплексни броеви:
z 1 = 12 + j 48 z2 = 12 - j48 z3= -12 + j 48 z4= -12 - j 48
Апсолутните вредности на сите четири броја се исти затоа што апсолутната вредност е независна од знаците. Само аглите се различни.
z1: = 12 + j * 48;
abs (z1) = [49.4773]
arc (z1) = [1.3258]
radtodeg (лак (z1)) = [75.9638]
z2: = 12-j * 48;
abs (z2) = [49.4773]
arc (z2) = [- 1.3258]
radtodeg (лак (z2)) = [- 75.9638]
z3: = - 12 + j * 48;
abs (z3) = [49.4773]
arc (z3) = [1.8158]
radtodeg (лак (z3)) = [104.0362]
z4: = - 12-j * 48:
abs (z4) = [49.4773]
arc (z4) = [- 1.8158]
radtodeg (лак (z4)) = [- 104.0362]
увезете математика како m
увезете cmath како в
z1=комплекс ('12+48j')
печатење (“abs(z1)=”,abs(z1))
печатење („лак(z1)=“, в.фаза(z1))
печатење(„степени(лак(z1))=“,м.степени(ц.фаза(z1)))
z2=комплекс ('12-48j')
печатење (“abs(z2)=”,abs(z2))
печатење („лак(z2)=“, в.фаза(z2))
печатење(„степени(лак(z2))=“,м.степени(ц.фаза(z2)))
z3=комплекс ('-12+48j')
печатење (“abs(z3)=”,abs(z3))
печатење („лак(z3)=“, в.фаза(z3))
печатење(„степени(лак(z3))=“,м.степени(ц.фаза(z3)))
z4=комплекс ('-12-48j')
печатење (“abs(z4)=”,abs(z4))
печатење („лак(z4)=“, в.фаза(z4))
печатење(„степени(лак(z4))=“,м.степени(ц.фаза(z4)))
Функцијата на лакот () на TINA го одредува аголот на кој било комплексен број, автоматски ставајќи го правилно во еден од четирите квадранти.
Бидете внимателни, сепак, со користење на тен-1 функција за наоѓање на аголот, бидејќи е ограничена на враќање на аглите само во првиот и четвртиот квадрант (–90 °φ<90 °)
Од z1 се наоѓа во првиот квадрант на координатниот систем, пресметката е:
α 1 = тен-1(48 / 12) = тен-1(4) = 75.96 °
Од z4 се наоѓа во третиот квадрант на координатниот систем, тен-1не го враќа аголот правилно. Пресметката на аголот е:
α 4 = 180 ° + 75.96 ° = 255.96 ° или -360 ° + 255.96 ° = - 104.04 °, што е исто што пресметува ТИНА.
z2 се наоѓа во четвртиот квадрант на координатниот систем. Пресметката на аголот е:
α 2 = тен-1(-48 / 12) = тен-1(-4) = -75.96 °
z3, сепак, е во 2nd квадрант на координатниот систем, па тен-1 не го враќа аголот правилно. Пресметката на аголот е:
α 3 = 180 ° -75.96 ° = 104.04 °.
Пример 4 Имаме два комплексни броеви: z1= 4 - j 6 и z2 = 5 ej45 ° .
Најди z3 = z1 + z2; z4 = z1 - z2; z5 = z1 * z2; z6 = z1 / z2
Прво го решаваме проблемот со помош на преведувачот на ТИНА
{Решение на толкувачот на ТИНА} |
Забележете како TINA лесно се справува со двата комплексни броеви дадени во различни форми.
Решението е покомплицирано без толкувачот. За да можеме да ги споредиме различните методи на множење и поделба, најпрво ќе ја утврдиме поларната форма на z1 и правоаголна форма на z2 .
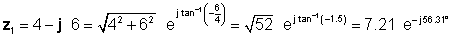
Следно, најнапред ги наоѓаме четирите решенија користејќи ги најлесните форми: правоаголни за додавање и одземање, и експоненцијална за множење и поделба:
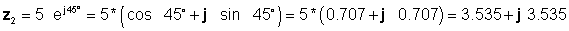
z 3 = z1 + z2 = 4 - j 6 + 3.535 + j 3.535 = 7.535 - j2.465
z 4 = z1 - z2 = 4 - j 6 - 3.535 - j 3.535 = 0.465 - j9.535
z 5 = z1 * z2 = 7.21 * 5 * ej(-56.31 ° + 45 °) = 36.05 e -j11.31 ° = 36.03 * (cos (-11.31 °) +j* грев (-11.31 °))
z 5 = 35.33 - j 7.07
z 6 = z1/z2= (7.21 / 5) * д j (-56.31 ° -45 °) = 1.442 e - j 101.31 ° = 1.442 (cos (-101.31 °))j* грев (-101.31 °))
z 6 = -0.2828 - j 1.414
кои се согласуваат со резултатите добиени со TINA преведувач.
Множењето извршено во правоаголна форма:
z 5 =z1*z2 = (4-j6) * 3.535 * (1 +j) = 7.07 * (2-j3) * (1 +j) = 7.07 * (2-j3+j2 + 3) = 7.07 * (5-j) = 35.35-j7.07
Конечно, поделбата извршена во правоаголна форма:
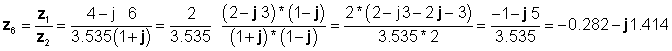
кои се согласуваат со претходните резултати.
