МЕСТО И МНОГУ ТЕКОВНИ МЕТОДИ

Кликнете или допрете ги Примерните кола подолу за да го повикате TINACloud и да го одберете интерактивниот DC режим за да ги анализирате Online.
Добијте низок пристап до TINACloud за да ги уредите примерите или да креирате сопствени кола

Друг начин за поедноставување на комплетниот комплет на равенките на Кирхоф е методот на струја на мрежест или јамка. Користејќи го овој метод, сегашниот закон на Кирхоф е задоволен автоматски, а равенките на јамките што ги пишуваме го задоволуваат и законот за напон на Кирхоф. Задоволување на тековниот закон на Кирхоф се постигнува со доделување на затворени јамки наречени мрежи или јамки на струјата на секоја независна јамка на колото и со користење на овие струи за да ги изрази сите други количини на колото. Бидејќи струите на јамката се затворени, струјата што се влева во јазол, исто така, мора да тече од јазолот; така што пишувањето на јазолските равенки со овие струи доведува до идентитет.

Дозволете ни прво да го разгледаме методот на струјни мрежи.

Прво забележуваме дека методот на струја на мрежи е применлив само за „рамни“ кола. Планетарните кола немаат жици за вкрстување кога се влечат во авион. Честопати, со прецртување на колото што се чини дека е нелитарно, можете да утврдите дека тој е, всушност, рамничар. За не-рамни кола, користете го тековен метод на јамка опишани подоцна во ова поглавје.

За да ја објасните идејата за струи на мрежи, замислете ги гранките на колото како „мрежа за риболов“ и доделете ја струја на решетката на секоја мрежа од мрежата. (Понекогаш се зборува и дека затворена јамка е назначена во секој „прозорец“ на колото.)

Шематски дијаграм 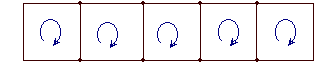"Рибарска мрежа" или графикон на коло

Техниката за претставување на колото со едноставен цртеж, наречен а графикон, е доста моќен. Од Законите на Кирхоф не зависат од природата на компонентите, можете да ги занемарите бетонските компоненти и да ги замените едноставните сегменти на линијата, наречени гранки на графиконот. Претставувањето на кола по графикони ни овозможува да ги користиме техниките на математички теорија на графикони. Ова ни помага да ја истражиме тополошката природа на едно коло и да ги утврдиме независните јамки. Врати се подоцна на оваа страница за да прочитате повеќе за оваа тема.

Чекорите на тековната анализа на мрежи:

1. Доделете ја струјата на решетката на секоја мрежа. Иако насоката е произволна, вообичаено е да се користи правецот на стрелките на часовникот.
   

2. Применувајте го законот за напон на Кирхоф (KVL) околу секоја мрежа, во иста насока како и струите на решетката. Ако отпорник има две или повеќе струјни мрежи низ него, вкупната струја низ резисторот се пресметува како алгебарска сума на струите на решетката. Со други зборови, ако струја што тече низ резисторот има иста насока како струјата на решетката на јамката, таа има позитивен знак, инаку негативен знак во сумата. Изворите на напон се земаат во предвид како и обично, Ако нивната насока е иста како и струјата на решетката, нивниот напон се смета за позитивен, инаку негативен, во равенките на KVL. Обично, за тековните извори, само една струја од мрежа се влева низ изворот, и таа струја има иста насока како струјата на изворот. Ако тоа не е случај, користете го поопштиот метод на тековната јамка, опишан подоцна во овој став. Нема потреба да се напишат равенки KVL за петелки што содржат мрежни струи доделени на тековни извори.
   

3. Решавање на добиените јамки равенки за мрежните струи.
   

4. Одредете ја бараната струја или напон во колото со употреба на струјни мрежи.

Да илустрираме методот по следниот пример:

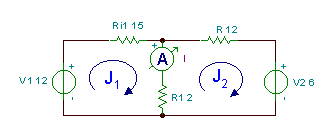
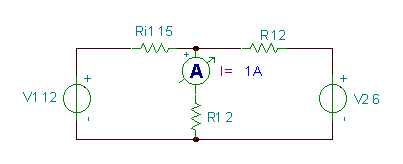
Најдете ја тековната јас во колото подолу.

Гледаме дека има две мрежи (или лев и десен прозорец) во ова коло. Ајде да ги назначиме струите на мрежната стрелка Ј₁ и Ј₂ до мрежите. Потоа ги пишуваме равенките на КВЛ, изразувајќи ги напоните преку отпорниците според законот на Ом:

-V₁ + Ј₁* (Р._i1+R₁) - Ј₂*R₁ = 0

V₂ - Џ₁*R₁ + Ј₂* (R + R₁) = 0

Нумерички:

-12 + J₁* 17 - J₂* 2 = 0

6 - Ј₁* 2 + J₂* 14 = 0

Експрес Ј₁ од првата равенка: J₁ = 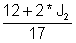и потоа заменете ја во втората равенка: 6 - 2 * + 14 * J₂ = 0

помножете се за 17: 102 - 24 + 4 * Ј₂ + 238 * Ј₂ = 0 оттука J₂ =

и Ј₁ =

Конечно, потребната струја:

Да ги провериме резултатите со ТИНА:

Следно, да го решиме претходниот пример повторно, но со поопшта метод на струјни јамки. Користејќи го овој метод, се повикуваат затворените тековни јамки јамки на јамка, се доделуваат не мора да на мрежите на колото, туку на произволни независни јамки. Може да се осигурате дека петелките се независни со тоа што имаат најмалку една компонента во секоја јамка што не е содржана во која било друга јамка. За рамни кола, бројот на независни јамки е ист како и бројот на мрежи, што е лесно да се види.

Поточен начин за одредување на бројот на независни јамки е како што следи.

Дадено коло со b гранки и N јазли Бројот на независните јамки l е:

l = b - N + 1

Ова произлегува од фактот дека бројот на независни равенки на Кирхоф мора да биде еднаков на гранките во колото и веќе знаеме дека има само N-1 независни јазол равенки. Затоа, вкупниот број на равенките на Кирхоф е

b = N-1 + l и оттаму l = b - N + 1

Оваа равенка, исто така, произлегува од основната теорема на теоријата на графикони, која ќе биде опишана подоцна на оваа страница.

Сега ајде да го решиме претходниот пример повторно, но поедноставно, со употреба на методот на тековната јамка. Со овој метод сме слободни да користиме јамки во мрежи или какви било други јамки, но ајде да ја задржиме јамката со J₁ во левата мрежа на колото. Сепак, за втората јамка ја избираме јамката со Ј_2, како што е прикажано на сликата подолу. Предноста на овој избор е тоа што Ј₁ ќе биде еднаква на бараната струја јас, бидејќи таа е единствената јамка на струја која минува низ R1. Ова значи дека не треба да го пресметуваме Ј2 воопшто. Забележете дека, за разлика од „вистинските“ струи, физичкото значење на јамките на јамката зависи од тоа како ги доделуваме на колото.

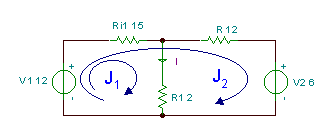
KVL равенките:

J1 * (Р.₁+R_i1) + J2 * R _i1 - V₁ = 0

-V₁+ J1 * R_i1+ J2 * (R + R_i) + V₂ = 0

и потребната струја: I = J₁

Numerically: J1*(15+2)+J2*15-12 = 0

-12 + J1 * 15 + J2 * (15 + 12) + 6 = 0

Експрес J2 од втората равенка:

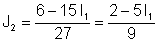
Замена во првата равенка:

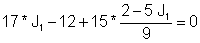
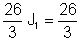
Оттука: J1 = I = 1 A

Дополнителни примери.

Пример 1

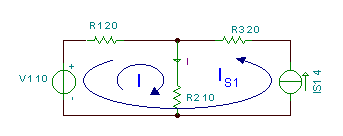
Најдете ја тековната јас во колото подолу.

Забележете дека насоката на оваа струјна јамка е не во насока на стрелките на часовникот, бидејќи нејзината насока е одредена од тековниот извор. Меѓутоа, бидејќи оваа струја во јамка е веќе позната, нема потреба да се напише равенката KVL за јамката каде I_S1 се зема.

Затоа, единствената равенка за решавање е:

-V₁ + I * R₂ + Р₁ * (Јас - јас_S1) = 0

оттука

I = (V₁ + Р₁ *I_S1) / (R₁ + Р₂)

Нумерички

I=(10+20*4)/(20+10)=3 A

Можете исто така да го генерирате овој резултат повикувајќи ја симболичката анализа на ТИНА од менито Резултати за анализа / симболичка анализа / ДЦ:

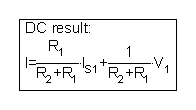
Или можете да ја решите равенката KVL од страна на толкувачот:

Следниот пример има 3 тековни извори и е многу лесен за решавање со методот на струја на јамка.

Пример 2

Пронајдете го напонот В.

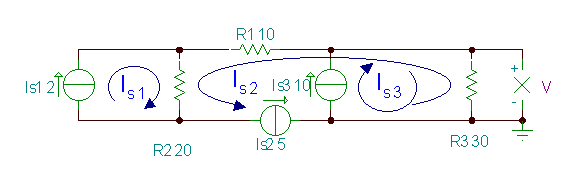
Во овој пример, можеме да избереме три струјни јамки, така што секој да помине низ само еден тековен извор. Затоа, сите три струја на јамка се познати, а ние треба само да го изразиме непознатиот напон, V, користејќи ги.

Изведба на алгебарската сума на струите преку Р.₃:

V = (I_S3 - Јас_S2) * Р₃= (10-5) * 30 = 150 V. Можете да го потврдите ова со ТИНА:.

Кликнете / допрете го горе наведеното коло за да ги анализирате on-line или кликнете на овој линк за да зачувате под Windows

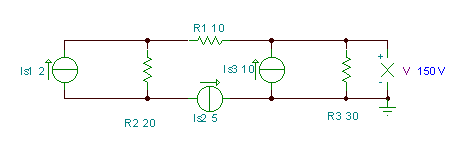
Следно, ајде повторно да решиме проблем што веќе го решивме во Кирхофските закони Јазол потенцијал метод поглавја.

Пример 3

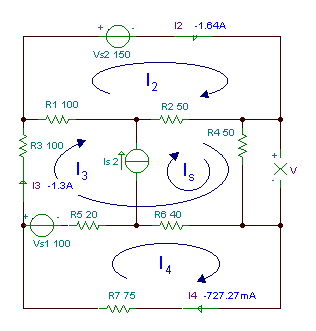
Пронајдете го напонот V на отпорот R₄.

Кликнете / допрете го горе наведеното коло за да ги анализирате on-line или кликнете на овој линк за да зачувате под Windows

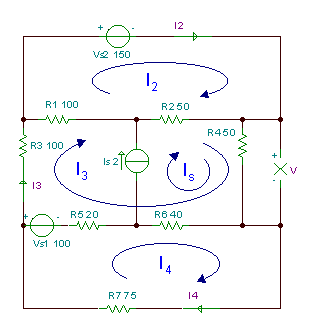
R₁ = Р₃ = 100 Ом, Р₂ = Р₄ = 50 Ом, Р₅ = 20 Ом, Р₆ = 40 Ом, Р₇ = 75 ohm.

За овој проблем се потребни најмалку 4 равенки за решавање во претходните поглавја.

Решавајќи го овој проблем со методот на струи на јамка, имаме четири независни јамки, но со правилен избор на струјни јамки, една од јамките на јамката ќе биде еднаква на струјата на изворот.

Врз основа на струите на јамката прикажани на сликата погоре, равенките на јамката се:

V_S1+I₄* (Р.₅+R₆+R₇) - Јас_S*R₆ -И₃* (Р.₅ + Р₆) = 0

V_S2 - Јас₃* (Р.₁+R₂) - Јас_S*R₂ + Јас₂* (Р.₁ + Р₂) = 0

-V_S1 + Јас₃* (Р.₁ + Р₂ + Р₃ + Р₄ + Р₅ + Р₆) + Јас_S* (Р.₂ +R₄ + Р₆) - Јас₄* (Р.₅ + Р₆) - Јас₂* (Р.₁ + Р₂) = 0

Непознатиот напон V може да се изрази со јачина на јамка:

V = R₄ * (I₂ + Јас₃)

Нумерички:

100 + I₄* 135-2 * 40-I₃* 60 = 0

150 + I₂* 150-2 * 50-I₃* 150 = 0

-100 + I₃* 360 + 2 * 140-I₄* 60-I₂* 150 = 0

V = 50 * (2 + I₃)

Можеме да го искористиме правилото на Крамер за да го решиме овој систем на равенки:

I₄ = D₃/D

каде што D е детерминанта на системот. D_4, детерминанта за јас_4, е формирана со замена на десната страна на системот е поставена за колоната на I₄коефициенти.

Систем на равенки во нарачана форма:

- 60 * јас₃ + 135 * I₄= -20

150 * I₂-150 * Јас₃ = - 50

-150 * Јас₂+ 360 * I₃ - 60 * I₄= - 180

Значи детерминанта D:

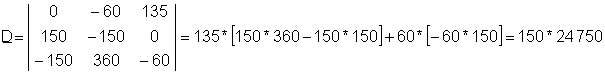
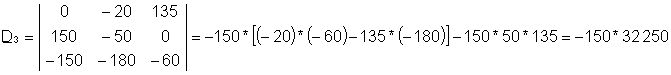
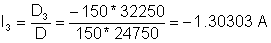
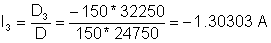
Решението на овој систем на равенки е:

V = R₄* (2 + I₃) = 34.8485 V

Одговорот можете да го потврдите преку резултатот пресметан од ТИНА.

Кликнете / допрете го горе наведеното коло за да ги анализирате on-line или кликнете на овој линк за да зачувате под Windows

Во овој пример, секоја непозната струја на јамка е струја на гранка (I1, I3 и I4); така што е лесно да се провери резултатот со споредба со резултатите од ДЦ анализата на ТИНА.