 Klõpsake või puudutage allpool asuvaid näidisahelaid, et kutsuda TINACloud ja valige interaktiivne alalisrežiim nende analüüsimiseks võrgus.
Klõpsake või puudutage allpool asuvaid näidisahelaid, et kutsuda TINACloud ja valige interaktiivne alalisrežiim nende analüüsimiseks võrgus. Saate madala hinnaga juurdepääsu TINACloud'ile, et muuta näiteid või luua oma ahelaid
Selles ja järgmistes peatükkides esitame väga olulise teema: vahelduvvoolu või vahelduvvoolu. Vahelduvvoolu nimetus ei ole väga täpne ja katab tavaliselt vooluahelaid, millel on sinusoidsed pinged ja voolud; aga võib vahelduvvool tähendada ka suvalist voolu lainekuju. Vahelduvvoolu pinge tähtsus on see, et seda tüüpi pinget kasutatakse peamiseks elektrienergia allikaks kodudes ja tööstuses kogu maailmas. See on ka aluseks paljudele elektroonika-, telekommunikatsiooni- ja tööstusrakendustele.
Sinusoidsete lainekujude ja nendega seotud ahelate käitlemiseks kasutame lihtsat ja elegantset meetodit, mida nimetatakse faasorite meetodiks. Fasorid põhinevad kompleksarvude omadustel, mis sobivad ideaalselt sinusoidsete koguste esindamiseks. Selles peatükis võtame kokku peamised faktid kompleksarvude ja nende toimingute kohta. Näitame ka, kuidas TINA tõlk tõlgendab keerukate numbritega arvutusi.
Keerulised numbrid koosnevad kahest osast, a tegelik osax), mis on tegelik arv ja nn kujuteldav osa (y), mis on reaalarv korrutatud 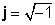
z = x + jy
kus 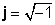
Keeruliste numbrite näited:
z 1 = 1 + j
z 2 = 4-2 j
z 3 = 3- 5j
Kompleksarvud toodi algselt kasutusele XVII sajandil, tähistamaks polünoomide juuri, mida ei olnud võimalik esindada ainuüksi reaalarvudega. Näiteks võrrandi x juured2 + 2x + 2 = 0i saab kirjeldada ainult kui 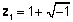
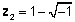
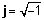
Keeruliste numbrite geomeetriline esitus
Ristkülikukujuline
Kuna keerulise arvu saab alati jagada selle tegelikeks ja keerulisteks osadeks, võime kompleksarvu esindada punktina kahemõõtmelisel tasapinnal. Kompleksse arvu tegelik osa on punkti projektsioon reaalteljele ja numbri kujutletav osa on projektsioon kujuteldavale teljele. Kui keerukas arv on esitatud tegelike ja kujuteldavate osade summana, siis öeldakse, et see on sees ristkülikukujuline or algebraline vorm.
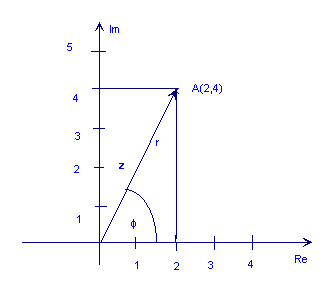
Järgnev joonis näitab kompleksi numbrit z = 2 + 4j
Polaarne ja eksponentsiaalne vorm
Nagu ülaltoodud jooniselt näete, võib punkti A tähistada ka noole pikkusega, r (nimetatakse ka absoluutväärtuseks, suuruseks või amplituudiks) ja selle nurk (või faas), φ positiivse horisontaaltelje suhtes vastupäeva. See on polaarne kompleksarvu kujul. Seda tähistatakse kui r ∠ φ.
Järgmine samm on väga oluline. Samuti võib sisestada polaarses vormis kompleksi numbri eksponentsiaalne vorm:
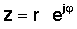
See lihtne väljend on eristatav selle poolest, et eksponendis on tavalise reaalarvu asemel kujuteldav arv. See keeruline eksponentsiaal käitub tõelise argumendiga väga erinevalt eksponentsiaalsest funktsioonist. Kuigi ex kasvab suurusjärgus x> 0 suurenedes kiiresti ja funktsiooni x <0 korral väheneb 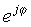
Euleri valem pakub ühtset seost ristkülikukujuliste, polaarsete ja eksponentsiaalsete kompleksarvude vormide vahel:
z = x + jy = re jφ = r (cos φ + j patt φ )
kus 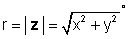
ja φ = tan-1 (y / x).
Ülaltoodud näite puhul z = 2 + 4j:
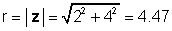
φ = tan-1 (4 / 2) = 63.4 °
seetõttu 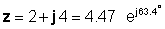
Või vastupidi:
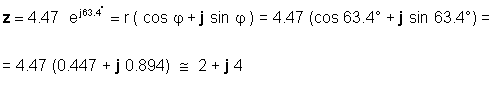
Sõltuvalt rakendusest peate mõlema vormi kasutamist oskama. Näiteks liitmist või lahutamist on ilmselgelt lihtsam teha, kui numbrid on ristkülikukujulised, samas kui korrutamist ja jagamist on lihtsam teha, kui numbrid on eksponentsiaalses vormis.
Toimingud keeruliste numbritega
Toimingud, mida saab teha keeruliste numbritega, on sarnased reaalarvudega. Allpool on kokku võetud eeskirjad ja mõned uued määratlused.
Toimingud j
Toimingud j lihtsalt järgige kujuteldava üksuse määratlust,


Kiireks ja täpseks töötamiseks peate need reeglid meelde jätma:
j 2 = -1
j 3 =-j
j 4 =1
1/j = -j
j2 = -1 lihtsalt järgneb 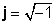
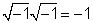
1i jaoks /j, korrutame 1 /jby j / j = 1 ja saada j/ (jj) = j / (- 1) = -j.
Kompleksne konjugaat
Kompleksse kompleksi keeruline konjugaat on kergesti tuletatav ja üsna oluline. Keerulise numbri keeruka konjugaadi saamiseks ristkülikukujulises vormis lihtsalt muutke kujuteldava osa märk. Selleks, et seda teha eksponentsiaalses vormis oleva numbri jaoks, muutke kompleksi numbri nurga märki, säilitades selle absoluutväärtuse sama.
Kompleksse kompleksi keeruline konjugaat z tähistatakse sageli z*.
Arvestades kompleksi numbrit z= a + jb on selle komplekskonjugaat z*= a– jb.
If z antakse eksponentsiaalses vormis, 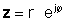
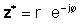
Ülaltoodud määratlusi kasutades on lihtne näha, et keeruline number, mis on korrutatud selle komplekskonjugaadiga, annab kompleksi numbri absoluutväärtuse ruudu:
zz* = r2 = a2 + b2
Samuti saame kompleksi numbri ja selle konjugaadi lisamise või lahutamise teel järgmised suhted:
z + z * = 2a
seetõttu
Re (z) = a = ( z + z * ) / 2
Sarnaselt:
z - z * =j2b
seetõttu
Im (z) = b = ( z -z * ) / 2j
Tõend:
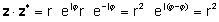
või tegelike ja kujuteldavate osade korrutamine ja kasutamine j2= -1
zz* = (a + jb) (a - jb) = a2+a jb - a jb - jbjb = a2j2 = a2 + b2
z + z* = a + jb + a - jb = 2a
z - z*= a + jb - a + jb =j2b
Numbrilised näited:
Ristkülikukujulises vormis:
z = 3 + j4
z* = 3– j4
zz * = 9 + 16 = 25
Polaarses vormis
z = 5 = 53.13 °
z * = 5 ~ 53.13 °
Eksponentsiaalses vormis:
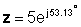
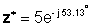
Liitmine ja lahutamine
Keeruliste arvude liitmine ja lahutamine on lihtne - me peame ainult reaalse ja kujuteldava osa eraldi lisama. Näiteks kui
z1 = 3 - 4j ja z2 = 2 + 3j
SIIS
z1 + z2 = 3 - 4j + 2 + 3j = 3 + 2 - 4j + 3j = 5 - j
z1 - z2 = 3 - 4j - 2 - 3j = 3 - 2 - 4j - 3j = 1 - j7
Ilmselt peaksime nende toimingute jaoks kasutama ristkülikukujulist vormi. Kui numbrid on antud eksponentsiaalses või polaarses vormis, peaksime need kõigepealt teisendama ristkülikukujuliseks, kasutades Euleri valemit, nagu on antud varem.
Korrutamine
Kompleksarvude korrutamiseks on kaks meetodit -
Keeruliste numbrite korrutamine ristkülikukujulisena
Operatsiooni teostamiseks korrutage lihtsalt ühe numbri tegelikud ja kujuteldavad osad teise numbri reaalsetest ja kujuteldavatest osadest ning kasutage identiteeti j2 = -1.
z1z2 = (a1 + jb1) (a2 + jb2) = a1 a2 + jb1a2+ jb2a1 - b1b2 = a1 a2- b1b2 + j(b1a2+ jb2a1)
Kui kompleksi numbrid on nummerdatud, ei ole ülaltoodud valemit vaja kasutada. Näiteks laske
z1 = 3 - 4j ja z2 = 2 + 3j
Komponentide otsese korrutamisega:
z1z2 = (3 - 4j) (2 + 3j) = 6-8j +9j + 12 = 18 + j
või kasutades valemit: z1z2 = a1 a2- b1b2 + j(b1a2+ b2a1)
z1z2 = 6 + 12 + j (-8 + 9) = 18 + j
Arvame, et kasutate valemit tõenäolisemalt, kui kasutate valemit kui siis, kui te korrutate komponendid otse.
z1: = 3-4 * j
z2: = 2 + 3 * j
z1 * z2 = [18 + 1 * j]
importida matemaatikat kui m
import cmath kui c
z1=kompleks('3-4j')
z2=kompleks('2+3j')
print(“z1*z2=”,z1*z2)
Polaarsetes või eksponentsiaalsetes vormides antud kompleksarvude korrutamine
Selle toimingu teostamiseks korrutage absoluutväärtused ja lisage kahe kompleksi numbri nurgad. Lase:
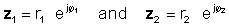
Seejärel kasutage eksponentsiaalsete funktsioonide korrutamise reeglit:
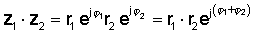
või polaarses vormis
z1 z2 = r1 r2 ∠ φ1 + φ2
Märkus: Me oleme seda reeglit juba kasutanud zz *ülalpool. Kuna konjugaadi nurgal on algsest kaldenurgast vastupidine märk, siis on tema enda konjugaadiga korrutatud kompleksarv alati reaalarv; nimelt selle absoluutväärtuse ruut: zz * = r2
Näiteks laske:
z1 = 5 ~ 30 ° ja z2 = 4 ∠ -60 °
SIIS
z1z2 = 20 ∠ -30 °
või eksponentsiaalses vormis
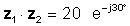
Korrutamine on ilmselgelt lihtsam, kui numbrid on polaarses või eksponentsiaalses vormis.
Kui keerulised numbrid on esitatud ristkülikukujuliselt, peaksite siiski kaaluma korrutamist otse, nagu ülal näidatud, sest kui arvud teisendatakse enne nende korrutamist polaarvormiks, on olemas ka täiendavad sammud. Teine tegur, mida tuleks kaaluda, on see, kas soovite, et vastused oleksid ristkülikukujulised või polaarsed / eksponentsiaalsed. Näiteks kui kaks numbrit on ristkülikukujulised, kuid soovite, et nende toode oleks polaarses vormis, on mõistlik need kohe teisendada ja seejärel korrutada.
jaotus
Kompleksarvude jagamiseks on kaks meetodit -
Keeruliste numbrite jagamine ristkülikukujulisena
Operatsiooni läbiviimiseks korrutage lugeja ja nimetaja nimetaja konjugaadiga. Nimetajast saab reaalarv ja jaotus taandatakse kahe keerulise arvu korrutamisele ning jagamine reaalarvuga, nimetaja absoluutväärtuse ruut.
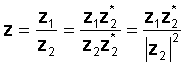
Näiteks laske:
z1 = 3 - 4j ja z2 = 2 + 3j
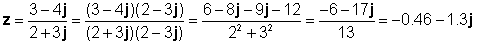
Vaatame selle tulemuse TINA tõlkega:
z1: = 3-4 * j
z2: = 2 + 3 * j
z1 / z2 = [- 461.5385m-1.3077 * j]
importida matemaatikat kui m
import cmath kui c
z1=kompleks('3-4j')
z2=kompleks('2+3j')
print(“z1/z2=”,z1/z2)
Polaarsetes või eksponentsiaalses vormis antud kompleksarvude jagamine
Operatsiooni läbiviimiseks jagage absoluutväärtused (suurused) ja lahutage nimetaja nurk lugeja nurga alt. Lase:
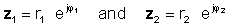
seejärel kasutatakse eksponentsiaalsete funktsioonide jagamise reeglit
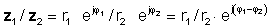
või polaarses vormis
z 1 / z2 = r1 / r2 ∠ φ 1- φ 2
Näiteks laske:
z 1 = 5 ∠ 30 ° ja z 2 = 2 ∠ -60 °
SIIS
z 1 / z2 = 2.5 = 90 °
või eksponentsiaalsetes ja ristkülikukujulistes vormides
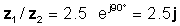
Vaatame selle tulemuse TINA tõlkega:
z1: = 5 * exp (j * degtorad (30))
z2: = 2 * exp (j * degtorad (-60))
z1 / z2 = [0 + 2.5 * j]
importida matemaatikat kui m
import cmath kui c
z1=5*(c.exp(kompleks(0,m.radiaanid(30))))
z2=2*(c.exp(kompleks(0,m.radiaanid(-60))))
print(“z1/z2=”,z1/z2)
Jagunemine on ilmselt lihtsam, kui numbrid on polaarses või eksponentsiaalses vormis.
Kui keerulised numbrid on esitatud ristkülikukujuliselt, peaksite siiski kaaluma jagamist otse komplekskonjugaatmeetodi abil, nagu ülal näidatud, kuna on veel täiendavaid samme, kui teisendate numbrid polaarseks vormiks enne nende jagamist. Teine tegur, mida tuleks kaaluda, on see, kas soovite, et vastused oleksid ristkülikukujulised või polaarsed / eksponentsiaalsed. Näiteks kui kaks numbrit on ristkülikukujulised, kuid soovite, et nende jagatis oleks polaarne, on mõistlik need kohe teisendada ja seejärel jagada.
Nüüd illustreerime keerukate numbrite kasutamist numbriliste probleemidega. Nagu tavaliselt, kontrollime meie lahendusi TINA tõlkega. Tõlk töötab radiaanidega, kuid tal on standardfunktsioonid radiaanide muutmiseks kraadideks või vastupidi.
Näiteks 1 Leidke polaarne esitus:
z = 12 - j 48
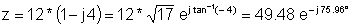
z: = 12-j * 48;
abs (z) = [49.4773]
kaar (z) = [- 1.3258]
radtodeg (kaar (z)) = [- 75.9638]
importida matemaatikat kui m
import cmath kui c
z=12-kompleks(48j)
print("abs(z)=",abs(z))
print("kaar(z)=",c.faas(z))
print(“degrees(arc(z))=”,m.degrees(c.phase(z)))
Näiteks 2 Leidke ristkülikukujuline kujutis:
z = 25 e j 125 °
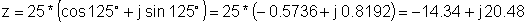
z: = 25 * exp (j * (degtorad (125)));
z = [- 14.3394 + 20.4788 * j]
Re (z) = [- 14.3394]
Im (z) = [20.4788]
importida matemaatikat kui m
import cmath kui c
z=25*c.exp(kompleks(0,m.radiaanid(125)))
print (“z=”,z)
print(“real(z)=”,z.real)
print(“imag(z)=”,z.imag)
Näiteks 3 Leidke järgmiste kompleksarvude polaarne esitus:
z 1 = 12 + j 48 z2 = 12 - j48 z3= -12 + j 48 z4= -12 - j 48
Kõigi nelja numbri absoluutväärtused on samad, kuna absoluutväärtus ei sõltu märkidest. Ainult nurgad on erinevad.
z1: = 12 + j * 48;
abs (z1) = [49.4773]
kaar (z1) = [1.3258]
radtodeg (kaar (z1)) = [75.9638]
z2: = 12-j * 48;
abs (z2) = [49.4773]
kaar (z2) = [- 1.3258]
radtodeg (kaar (z2)) = [- 75.9638]
z3: = - 12 + j * 48;
abs (z3) = [49.4773]
kaar (z3) = [1.8158]
radtodeg (kaar (z3)) = [104.0362]
z4: = - 12-j * 48:
abs (z4) = [49.4773]
kaar (z4) = [- 1.8158]
radtodeg (kaar (z4)) = [- 104.0362]
importida matemaatikat kui m
import cmath kui c
z1=kompleks('12+48j')
print("abs(z1)=",abs(z1))
print("kaar(z1)=",c.faas(z1))
print(“degrees(arc(z1))=”,m.degrees(c.phase(z1)))
z2=kompleks('12-48j')
print("abs(z2)=",abs(z2))
print("kaar(z2)=",c.faas(z2))
print(“degrees(arc(z2))=”,m.degrees(c.phase(z2)))
z3=kompleks('-12+48j')
print("abs(z3)=",abs(z3))
print("kaar(z3)=",c.faas(z3))
print(“degrees(arc(z3))=”,m.degrees(c.phase(z3)))
z4=kompleks('-12-48j')
print("abs(z4)=",abs(z4))
print("kaar(z4)=",c.faas(z4))
print(“degrees(arc(z4))=”,m.degrees(c.phase(z4)))
TINA kaare () funktsioon määrab mis tahes keeruka numbri nurga, paigutades selle automaatselt õigesti ühte neljast kvadrandist.
Olge ettevaatlik, aga kasutage tan-1 funktsioon nurga leidmiseks, kuna see piirdub tagasipöörduvate nurkadega ainult esimeses ja neljandas kvadrandis (–90 °φ<90 °).
Alates z1 asub koordinaatsüsteemi esimeses kvartalis, arvutatakse:
α 1 = tan-1(48 / 12) = tan-1(4) = 75.96 °
Alates z4 asub koordinaatsüsteemi kolmandas kvartalis, tan-1ei tagasta nurka õigesti. Nurkade arvutus on:
α 4 = 180 ° + 75.96 ° = 255.96 ° või -360 ° +255.96 ° = - 104.04 °, mis on sama, mis TINA arvutas.
z2 asub koordinaatsüsteemi neljandas kvartalis. Nurkarvutus on:
α 2 = tan-1(-48 / 12) = tan-1(-4) = -75.96 °
z3, aga on koordinaatide süsteemi 2nd kvartalis, nii tan-1 ei tagasta nurka õigesti. Nurkade arvutus on:
α 3 = 180 ° -75.96 ° = 104.04 °.
Näiteks 4 Meil on kaks keerulist numbrit: z1= 4 - j 6 ja z2 = 5 ej45 ° .
leidma z3 = z1 + z2; z4 = z1 - z2; z5 = z1 * z2; z6 = z1 / z2
Kõigepealt lahendame probleemi TINA tõlkega
{TINA tõlgi lahendus} |
Pange tähele, kuidas TINA käsitseb kahes erinevas vormis esitatud kompleksi numbrit.
Ilma tõlgita on lahendus keerulisem. Nii et saaksime võrrelda erinevaid korrutamis- ja jagamismeetodeid, määrame kõigepealt polaarse vormi z1 ja ristkülikukujuline vorm z2 .
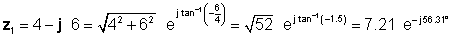
Järgmisena leiame neli lahendust, kasutades kõigepealt lihtsamaid vorme: ristkülikukujulised liitmiseks ja lahutamiseks ning eksponentsiaalsed korrutamisel ja jagamisel:
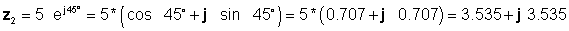
z 3 = z1 + z2 = 4 - j 6 + 3.535 + j 3.535 = 7.535 - j2.465
z 4 = z1 - z2 = 4 - j 6 - 3.535 - j 3.535 = 0.465 - j9.535
z 5 = z1 * z2 = 7.21 * 5 * ej(-56.31 ° + 45 °) = 36.05 e -j11.31 ° = 36.03 * (cos (-11.31 °) +)j* sin (-11.31 °))
z 5 = 35.33 - j 7.07
z 6 = z1/z2= (7.21 / 5) * e j (-56.31 ° -45 °) = 1.442 e - j 101.31 ° = 1.442 (cos (-101.31 °) +)j* sin (-101.31 °))
z 6 = -0.2828 - j 1.414
mis nõustuvad TINA tõlkega saadud tulemustega.
Ristkülikukujuline korrutamine:
z 5 =z1*z2 = (4-j6) * 3.535 * (1 +j) = 7.07 * (2-j3) * (1 +j) = 7.07 * (2-j3+j2 + 3) = 7.07 * (5-j) = 35.35-j7.07
Lõpuks jagunemine ristkülikukujulises vormis:
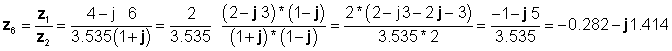
mis on eelnevate tulemustega nõus.
