 Կտտացրեք կամ Ստուգեք Ստորին օրինակելի սխեմաները, TINACloud- ին կանչելու համար եւ ընտրեք Interactive DC ռեժիմը `դրանք վերլուծելու համար:
Կտտացրեք կամ Ստուգեք Ստորին օրինակելի սխեմաները, TINACloud- ին կանչելու համար եւ ընտրեք Interactive DC ռեժիմը `դրանք վերլուծելու համար: Ստացեք ցածր գներով մուտք դեպի TINACloud, օրինակները խմբագրել կամ ստեղծել ձեր սեփական սխեմաները
Այս եւ հաջորդ գլուխներում մենք կներկայացնենք շատ կարեւոր թեման, AC կամ փոփոխվող ընթացիկ: Անունը փոխարինող հոսանքը շատ հստակ չէ եւ սովորաբար ծածկում է սինուսոիդային հոսանքների եւ հոսանքների սխեմաները. սակայն փոխարինող տերմինը կարող է նաեւ նշանակել ցանկացած կամայական ընթացիկ ալիքի ձեւ: AC լարման կարեւորությունը այն է, որ նման լարումը օգտագործվում է տների եւ արդյունաբերության հիմնական էլեկտրաէներգիայի աղբյուրի համար ամբողջ աշխարհում: Դա նաեւ հիմք է բազմաթիվ էլեկտրոնիկայի, հեռահաղորդակցության եւ արդյունաբերական ծրագրերի համար:
Սինուսոիդային ալիքի ձեւերի եւ դրանց հետ կապված սխեմաների գործածման համար մենք կօգտագործենք պարզ եւ էլեգանտ մեթոդ, որը կոչվում է ֆազորների մեթոդ: Ֆազերը հիմնված են բարդ թվերի հատկությունների վրա, որոնք իդեալական են սինուսոիդային քանակների ներկայացման համար: Այս գլխում մենք ամփոփում ենք բարդ թվերի եւ դրանց գործառնությունների մասին հիմնական փաստերը: Մենք նաեւ ցույց կտանք, թե ինչպես TINA- ի թարգմանիչը հեշտացնում է հաշվարկներ կատարել համալիր թվերով:
Համալիր համարները բաղկացած են երկու մասից, ա իրական մասը (x), որը իրական թիվ է եւ այսպես կոչված երեւակայական մասը (y), որը իսկական թիվ է բազմապատկած 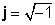
z = x + jy
որտեղ 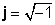
Բարդ թվերի օրինակներ.
z 1 = 1 + j
z 2 = 4-2 j
z 3 = 3- 5j
Բարդ թվերը սկզբնապես ներկայացվել են տասնյոթերորդ դարում ՝ բազմամոլների արմատները ներկայացնելու համար, որոնք միայն իրական թվերով չէին կարող ներկայացվել: Օրինակ ՝ x հավասարման արմատները2 + 2x + 2 = 0- ը կարող է նկարագրվել որպես միայն 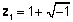
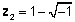
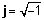
Բարդ թվերի երկրաչափական ներկայացում
Ուղղանկյուն ձեւ
Քանի որ բարդ թիվը միշտ կարող է տարանջատվել իր իրական և բարդ մասերի մեջ, մենք կարող ենք բարդ համարը ներկայացնել որպես կետ երկաչափ հարթության վրա: Բարդ համարի իրական մասը կետի պրոյեկտումն է իրական առանցքի վրա, իսկ համարի երևակայական մասը երևակայական առանցքի վրա պրոյեկտն է: Երբ բարդ թիվը ներկայացված է որպես իրական և երևակայական մասերի գումար, մենք ասում ենք, որ այն գտնվում է ուղղանկյուն or հանրահաշվական ձեւ.
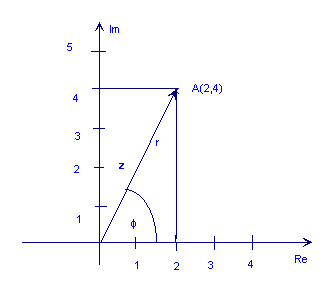
Հետեւյալ նկարը ցույց է տալիս համալիրի համարը z = 2 + 4j
Բեւեռային եւ արտապատկերային ձեւ
Ինչպես տեսնում եք վերը նկարից, A կետը կարող է ներկայացվել նաև սլաքի երկարությամբ, r (կոչվում է նաև բացարձակ արժեք, մեծություն կամ լայնություն) և դրա անկյունը (կամ փուլը), φ հարաբերական `հակառակ սլաքի ուղղությամբ դեպի դրական հորիզոնական առանցք: Սա է բեւեռ բարդ թվի ձև: Նշվում է որպես r φ.
Հաջորդ քայլը շատ կարեւոր է: Բեւեռային ձեւով համալիր թիվ կարելի է գրել նաեւ ցուցադրական ձեւ:
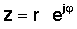
Այս պարզ արտահայտությունն առանձնահատուկ է նրանով, որ իր մեջ երևակայական թիվ ունի սովորական իրական համարի փոխարեն: Այս բարդ էքսպոնենցիալը շատ տարբերվում է էքսպոնենցիալ գործառույթից ՝ իրական փաստարկով: Մինչ եx աճում է արագությամբ մեծությամբ x> 0 մեծացնելու համար և նվազում x <0 ֆունկցիան 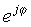
Euler- ի բանաձեւը ապահովում է միացնող կապ `համալիր թվերի ուղղանկյուն, բեւեռային եւ արտապատկերային ձեւերի միջեւ.
z = x + jy = կրկին jφ = r (cos φ + j առանց φ )
որտեղ 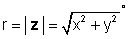
և φ = tan-1 (y / x):
Վերոնշյալ մեր օրինակին համար, z = 2 + 4j:
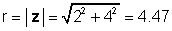
φ = tan-1 (4 / 2) = 63.4 °
հետեւաբար 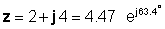
Կամ հակառակը.
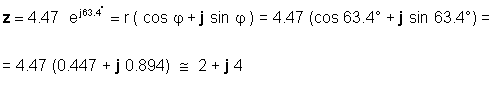
Անհրաժեշտ կլինի զգույշ լինել երկու ձևերի օգտագործման վրա ՝ կախված դիմումից: Օրինակ, հավելումն կամ հանումը ակնհայտորեն ավելի հեշտ է անել, երբ թվերը ուղղանկյուն ձևի մեջ են, մինչդեռ բազմապատկումը և բաժանումը ավելի հեշտ է անել, երբ թվերը գտնվում են էքսպոնենտալ վիճակում:
Գործառնություններ համալիր թվերով
Գործառույթները, որոնք կարելի է կատարել բարդ թվերով, նման են իրական թվերի: Կանոնները և որոշ նոր սահմանումներ ամփոփված են ստորև:
Գործարքներ j
Գործողություններ j պարզապես հետեւեք երեւակայական միավորի սահմանմանը,


Կարող են աշխատել արագ եւ ճշգրիտ, դուք պետք է անգիր այս կանոնները:
j 2 = -1
j 3 =-j
j 4 =1
1/j = -j
j2 = -1 պարզապես պարզվում է 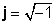
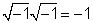
1 /j, մենք բազմապատկում ենք 1 /jby j / j = 1 եւ ստացեք j/ (ժժ) = j / (- 1) = -j.
Կոմբինացված համադրություն
Համալիր համալիրի բարդ կոնվուլտուրան հեշտությամբ բխում է եւ շատ կարեւոր է: Ուղղանկյուն ձեւով համալիրի համալիրի համադրություն ձեռք բերելու համար պարզապես փոխեք պատկերային մասի նշանը: Որպեսզի դա ցույց տա, որ մի շարք էքսպոնենցիալ ձեւով, փոխեք բարդի համարի անկյունը, իսկ բացարձակ արժեքը նույնը պահելով:
Համալիր բարդի համադրություն z հաճախ նշվում է z*.
Հաշվի առնելով համալիրը z= a + jբ, դրա բարդ կոնվիգատանն է z*= a- jb.
If z ներկայացվում է exponential ձեւով, 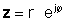
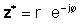
Օգտագործելով վերը նշված հասկացությունները, հեշտ է տեսնել, որ համալիրի բազմապատիկը իր բազմապատկված համատեքստով բազմապատկվում է `համալիրի բացարձակ արժեքի քառակուսին.
zz* = r2 = ա2 + b2
Բացի այդ, ավելացնելով կամ հանել ցանկացած բարդ թվաքանակի եւ դրա համադրությունը, մենք ստանում ենք հետեւյալ հարաբերությունները.
z + z * = 2a
հետեւաբար
Re (z) = a = ( z + z * ) / 2
Նմանապես `
z - z * =j2b
հետեւաբար
Ես(z) = b = ( z -z * ) / 2j
Ապացուցված է.
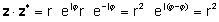
կամ բազմապատկելով իրական եւ երեւակայական մասերը եւ օգտագործելով j2= -1
zz* = (a + jբ) (ա - jբ) = ա2+a jբ - ա jբ - jbjb = a2j2 = ա2 + b2
z + z* = a + jb + a - jb = 2a
z - z*= a + jբ - ա + jբ =j2b
Թվային օրինակներ.
Ուղղանկյուն ձեւով.
z = 3 + j4
z* = 3- j4
zz * = 9 + 16 = 25
Բեւեռային ձեւով
z = 5 ∠ 53.13 °
z * = 5 ∠- 53.13 °
Արտոնագրային ձեւով.
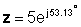
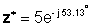
Լրացում և հանում
Բարդ թվերի լրումն ու հանումը պարզ է. Մեզ հարկավոր է միայն ավելացնել իրական և երևակայական մասերը: Օրինակ, եթե
z1 = 3 - 4j և z2 = 2 + 3j
ապա
z1 + z2 = 3 - 4j + 2 + 3j = 3 + 2 - 4j + 3j = 5 - j
z1 - z2 = 3 - 4j - 2 - 3j = 3 - 2 - 4j - 3j = 1 - j7
Ակնհայտ է, որ այս գործողությունների համար մենք պետք է օգտագործենք ուղղանկյուն ձև: Եթե համարները տրված են էքսպոզիցիոն կամ բևեռային տեսքով, ապա մենք դրանք առաջին հերթին պետք է վերածենք ուղղանկյուն ձևի ՝ օգտագործելով Euler's բանաձևը, ինչպես տրված է ավելի վաղ:
Բազմապատկում
Բարդ թվերի բազմապատկման երկու եղանակ կա.
Ուղղանկյուն ձեւով տրված բարդ թվերի բազմապատկում
Գործողությունը իրականացնելու համար պարզապես բազմապատկեք մեկ համարի իրական և երևակայական մասերը, իր հերթին, մյուս համարի իրական և երևակայական մասերով և օգտագործեք ինքնությունը j2 = -1:
z1z2 = (ա1 + jb1) (ա2 + jb2) = a1 a2 + jb1a2+ jb2a1 - բ1b2 = ա1 a2- բ1b2 + j(b1a2+ jb2a1)
Երբ բարդ թվերը տրվում են թվային, անհրաժեշտ չէ օգտագործել վերը նշված բանաձեւը: Օրինակ `թող
z1 = 3 - 4j և z2 = 2 + 3j
Ուղղակի բազմապատկելով բաղադրիչները `
z1z2 = (3 - 4j) (2 + 3j) = 6- 8j +9j + 12 = 18 + j
կամ օգտագործելով բանաձեւը. z1z2 = ա1 a2- բ1b2 + j(b1a2+ B2a1)
z1z2 = 6 + 12 + j (-8 + 9) = 18 + j
Մենք կարծում ենք, որ ավելի մեծ հավանականություն կունենաք, եթե դուք օգտագործում եք բանաձեւը, եթե դուք ուղղակիորեն բազմապատկեք բաղադրիչները:
z1: = 3-4 * ժ
z2: = 2 + 3 * ժ
z1 * z2 = [18 + 1 * ժ]
ներմուծել մաթեմատիկան որպես մ
ներմուծել cmath որպես c
z1=բարդ ('3-4j')
z2=բարդ ('2+3j')
տպել (“z1*z2=”,z1*z2)
Բեւեռային կամ ցուցադրական ձեւով տրված բարդ թվերի բազմապատկում
Այս գործողությունը իրականացնելու համար ավելացրեք բացարձակ արժեքները եւ ավելացրեք երկու բարդ թվերի անկյունները: Թողեք.
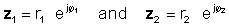
Այնուհետեւ օգտագործում էքսպոնենտալ գործառույթների բազմապատկման կանոն.
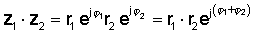
կամ բեւեռային ձեւով
z1 z2 = r1 r2 Φ1 + φ2
Նշում. Մենք հաշվարկել ենք այս կանոնը zz *վերևում: Քանի որ կոնյունգատի անկյունն ունի բնօրինակ անկյունի հակառակ նշան, ապա իր սեփական կոնյուկատներով բազմապատկված բարդ թիվը միշտ իսկական թիվ է. մասնավորապես ՝ դրա բացարձակ արժեքի քառակուսին. zz * = r2
Օրինակ, թույլ տվեք.
z1 = 5 ∠ 30 ° և z2 = 4 ∠ -60 °
ապա
z1z2 = 20 ∠ -30 °
կամ արտոնագրային ձեւով
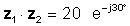
Բազմապատկումը ակնհայտորեն ավելի պարզ է, երբ թվերը բեւեռային կամ արտապատկերային ձեւով են:
Այնուամենայնիվ, եթե բարդ համարները տրված են ուղղանկյուն ձևով, ապա պետք է հաշվի առնեք բազմապատկումը ուղղակիորեն կատարելը, ինչպես ցույց է տրված վերևում, քանի որ կան լրացուցիչ քայլեր, եթե դրանք բազմապատկելուց առաջ փոխեք թվերը բևեռային ձևի: Քննարկման մեկ այլ գործոն նաև այն է, որ դուք ուզում եք, որ պատասխանները լինեն ուղղանկյուն տեսքով, կամ բևեռային / էքսպոզիցիոն ձևով: Օրինակ, եթե երկու համարները ուղղանկյուն տեսքով են, բայց կցանկանայիք, որ դրանց արտադրանքը բևեռային տեսքով, իմաստ ունի դրանք անմիջապես փոխարկել, ապա բազմապատկել:
բաժին
Բարդ թվերի բաժանման երկու եղանակ կա.
Ուղղանկյուն ձեւով տրված բարդ թվերի բաժին
Գործողությունը իրականացնելու համար բազմապատկեք համարիչը և նշանակիչը `նշողի կոնյուգատի միջոցով: Դիմորդը դառնում է իրական թիվ, իսկ բաժանումը կրճատվում է երկու բարդ թվերի բազմապատկման վրա և բաժանում իրական թվով ՝ նշանակողի բացարձակ արժեքի քառակուսի:
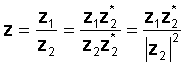
Օրինակ `
z1 = 3 - 4j և z2 = 2 + 3j
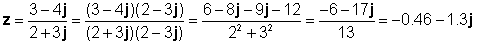
Այս արդյունքը ստուգենք TINA- ի թարգմանչի հետ.
z1: = 3-4 * ժ
z2: = 2 + 3 * ժ
z1 / z2 = [- 461.5385m-1.3077 * ժ]
ներմուծել մաթեմատիկան որպես մ
ներմուծել cmath որպես c
z1=բարդ ('3-4j')
z2=բարդ ('2+3j')
տպել (“z1/z2=”,z1/z2)
Բեւեռային կամ արտոնագրային ձեւով տրված բարդ թվերի բաժին
Գործողությունը իրականացնելու համար բաժանեք բացարձակ արժեքները (մագնիտուդներ) եւ վերցրեք դինոմինատորի անկյունը, նահանջի տեսանկյունից: Թողեք.
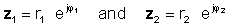
ապա օգտագործելով արտոնյալ գործառույթների բաժանման կանոնը
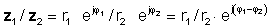
կամ բեւեռային ձեւով
z 1 / z2 = r1 / r2 ∠ φ 1- φ 2
Օրինակ, թույլ տվեք.
z 1 = 5 ∠ 30 ° և z 2 = 2 ∠ -60 °
ապա
z 1 / z2 = 2.5 ∠ 90 °
կամ երկրաչափական եւ ուղղանկյուն ձեւերով
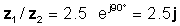
Այս արդյունքը ստուգենք TINA- ի թարգմանչի հետ.
z1: = 5 * exp (ժ * degtorad (30))
z2: = 2 * exp (ժ * degtorad (-60))
z1 / z2 = [0 + 2.5 * ժ]
ներմուծել մաթեմատիկան որպես մ
ներմուծել cmath որպես c
z1=5*(c.exp(complex(0,m.radians(30))))
z2=2*(c.exp(complex(0,m.radians(-60))))
տպել (“z1/z2=”,z1/z2)
Բաժանումը ակնհայտորեն ավելի պարզ է, երբ թվերը բևեռային կամ էքսպոզիցիոն ձևով են:
Այնուամենայնիվ, եթե բարդ համարները տրված են ուղղանկյուն ձևով, ապա դուք պետք է հաշվի առնեք բաժանումը ուղղակիորեն օգտագործելով բարդ կոնյուգատային մեթոդ, ինչպես ցույց է տրված վերևում, քանի որ կան լրացուցիչ քայլեր, եթե դրանք բաժանելուց առաջ թվերը փոխեք բևեռային ձևի: Քննարկման մեկ այլ գործոն նաև այն է, որ դուք ուզում եք, որ պատասխանները լինեն ուղղանկյուն տեսքով, կամ բևեռային / էքսպոզիցիոն ձևով: Օրինակ, եթե երկու համարները ուղղանկյուն վիճակում են, բայց կցանկանայիք, որ դրանց քամիչը բևեռային տեսքով լիներ, իմաստ ունի դրանք անմիջապես փոխարկել, ապա բաժանել:
Այժմ եկեք ցույց տանք, որ համալիր թվերի օգտագործումը ավելի շատ թվային խնդիրներ է: Ինչպես միշտ, մենք ստուգելու ենք մեր լուծումները TINA- ի թարգմանչի միջոցով: Թարգմանիչը աշխատում է ռադիացիների հետ, սակայն այն ունի ստանդարտ ֆունկցիան ռադիանցի փոխակերպման աստիճանին կամ հակառակը:
Օրինակ 1 Գտեք բեւեռային ներկայացուցչությունը.
z = 12 - j 48
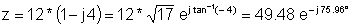
z: = 12-j * 48;
abs (z) = [49.4773]
arc (z) = [- 1.3258]
radtodeg (arc (z)) = [- 75.9638]
ներմուծել մաթեմատիկան որպես մ
ներմուծել cmath որպես c
z=12-բարդ (48j)
տպել («abs(z)=», abs(z))
տպել («arc(z)=», c.phase(z))
տպել («աստիճաններ (arc(z))=», m.degrees(c.phase(z)))
Օրինակ 2 Գտեք ուղղանկյուն ներկայացուցչությունը.
z = 25 էլ j 125 °
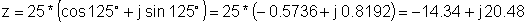
z: = 25 * exp (ժ * (degtorad (125)));
z = [- 14.3394 + 20.4788 * ժ]
Re (z) = [- 14.3394]
Իմ (z) = [20.4788]
ներմուծել մաթեմատիկան որպես մ
ներմուծել cmath որպես c
z=25*c.exp(complex(0,m.radians(125)))
տպել (“z=”, z)
տպել («իրական (z)=», z.real)
տպել («imag(z)=»,z.imag)
Օրինակ 3 Գտեք հետեւյալ բարդ թվերի բեւեռային ներկայացուցչությունը.
z 1 = 12 + j 48 z2 = 12 - j48 z3= -12 + j 48 z4= -12 - j 48
Բոլոր չորս համարների բացարձակ արժեքները նույնն են, քանի որ բացարձակ արժեքը անկախ է նշաններից: Միայն անկյունները տարբեր են:
z1: = 12 + j * 48;
abs (z1) = [49.4773]
arc (z1) = [1.3258]
radtodeg (arc (z1)) = [75.9638]
z2: = 12-j * 48;
abs (z2) = [49.4773]
arc (z2) = [- 1.3258]
radtodeg (arc (z2)) = [- 75.9638]
z3: = - 12 + j * 48;
abs (z3) = [49.4773]
arc (z3) = [1.8158]
radtodeg (arc (z3)) = [104.0362]
z4: = - 12-j * 48:
abs (z4) = [49.4773]
arc (z4) = [- 1.8158]
radtodeg (arc (z4)) = [- 104.0362]
ներմուծել մաթեմատիկան որպես մ
ներմուծել cmath որպես c
z1=բարդ ('12+48j')
տպել ("abs(z1)=",abs(z1))
տպել ("arc(z1)=",c.phase(z1))
տպել («աստիճաններ (arc(z1))=», m.degrees(c.phase(z1)))
z2=բարդ ('12-48j')
տպել ("abs(z2)=",abs(z2))
տպել ("arc(z2)=",c.phase(z2))
տպել («աստիճաններ (arc(z2))=», m.degrees(c.phase(z2)))
z3=բարդ ('-12+48j')
տպել ("abs(z3)=",abs(z3))
տպել ("arc(z3)=",c.phase(z3))
տպել («աստիճաններ (arc(z3))=», m.degrees(c.phase(z3)))
z4=բարդ ('-12-48j')
տպել ("abs(z4)=",abs(z4))
տպել ("arc(z4)=",c.phase(z4))
տպել («աստիճաններ (arc(z4))=», m.degrees(c.phase(z4)))
TINA- ի կամարի () գործառույթը որոշում է ցանկացած բարդ համարի անկյունը ՝ ավտոմատ կերպով այն ճիշտ տեղադրելով չորս քառանկյուններից մեկում:
Ուշադիր եղեք, սակայն օգտագործելով tan- ը-1 անկյունը գտնելու գործառույթ, քանի որ այն սահմանափակվում է միայն առաջին և չորրորդ քառորդներում (–90 °φ<90 °)
Հետո z1 գտնվում է կոորդինատային համակարգի առաջին քառադանում, հաշվարկը հետեւյալն է.
α 1 = tan-1(48 / 12) = տան-1(4) = 75.96 °
Հետո z4 գտնվում է կոորդինատների համակարգի երրորդ կադաստրում, tan-1չի վերադարձնում անկյունը ճիշտ: Անկյունի հաշվարկը հետեւյալն է.
α 4 = 180 ° + 75.96 ° = 255.96 ° կամ -360 ° + 255.96 ° = - 104.04 °, ինչը նույնն է, ինչ հաշվարկված է TINA- ի կողմից:
z2 գտնվում է կոորդինատային համակարգի չորրորդ կադաստրում: Անկյունի հաշվարկը հետեւյալն է.
α 2 = tan-1(-48 / 12) = տան-1(-4) = -75.96 °
z3, սակայն, գտնվում է համակարգային համակարգի 2nd քառակուսի մեջ, այսինքն, tan-1 անկյունը ճիշտ չի վերադարձնում: Անկյունի հաշվարկը հետեւյալն է.
α 3 = 180 ° -75.96 ° = 104.04 °.
Օրինակ 4 Մենք ունենք երկու բարդ թվեր. z1= 4 - j 6 եւ z2 = 5 էլj45 ° .
Գտնել z3 = z1 + z2; z4 = z1 - z2; z5 = z1 * z2; z6 = z1 / z2
Նախ, մենք լուծում ենք խնդիրը, օգտագործելով TINA- ի թարգմանիչը
{TINA- ի թարգմանչի լուծում} |
Ուշադրություն դարձրեք, թե ինչպես TINA- ն հեշտորեն գործադրում է տարբեր ձեւերով տրված երկու բարդ թվերը:
Լուծումը ավելի բարդ է առանց թարգմանչի: Որպեսզի մենք կարողանանք համեմատել բազմապատկման և բաժանման տարբեր մեթոդներ, նախ որոշելու ենք բևեռային ձևը z1 եւ ուղղանկյուն ձեւը z2 .
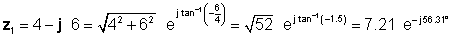
Հաջորդը, մենք գտնում ենք չորս լուծումները `առաջին հերթին օգտագործելով ամենահեշտ ձևերը` ուղղանկյուն հավելման և հանման համար, և բազմացման և բաժանման էքսպոնենտալ:
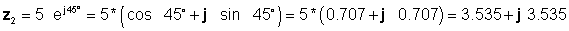
z 3 = z1 + z2 = 4 - j 6 + 3.535 + j 3.535 = 7.535 - j2.465
z 4 = z1 - z2 = 4 - j 6 - 3.535 - j 3.535 = 0.465 - j9.535
z 5 = z1 * z2 = 7.21 * 5 * ej(-56.31 ° + 45 °) = 36.05 էլ -j11.31 ° = 36.03 * (cos (-11.31 °) +)j* մեղ (-11.31 °))
z 5 = 35.33 - j 7.07
z 6 = z1/z2= (7.21 / 5) * e j (-56.31 ° -45 °) = 1.442 էլ - j 101.31 ° = 1.442 (cos (-101.31 °) +)j* մեղ (-101.31 °))
z 6 = -0.2828 - j 1.414
որոնք համամիտ են TINA թարգմանչի հետ ձեռք բերված արդյունքների հետ:
Ուղղանկյուն ձեւով կատարված բազմապատկումը.
z 5 =z1*z2 = (4-j6) * 3.535 * (1 +j) = 7.07 * (2-j3) * (1 +j) = 7.07 * (2-j3+j2 + 3) = 7.07 * (5-j) = 35.35-j7.07
Վերջապես բաժանումը ուղղանկյուն ձեւով կատարվեց.
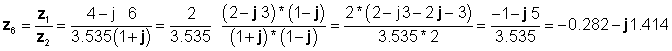
որոնք համամիտ են նախորդ արդյունքների հետ:

