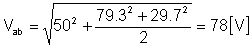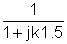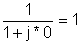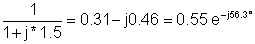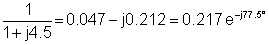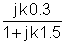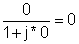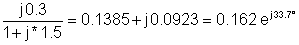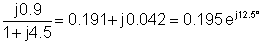Klik of Tik op de onderstaande Voorbeeldcircuits om TINACloud op te roepen en selecteer de interactieve DC-modus om ze online te analyseren. Krijg een goedkope toegang tot TINACloud om de voorbeelden te bewerken of om uw eigen circuits te maken
De Fourier-stelling stelt dat elke periodieke golfvorm kan worden gesynthetiseerd door de juiste gewogen sinus- en cosinustermen van verschillende frequenties toe te voegen. De stelling wordt goed behandeld in andere leerboeken, dus we zullen alleen de resultaten samenvatten en enkele voorbeelden laten zien.
Laat onze periodieke functie f (t) = f (t zijn ±nT) waarbij T de tijd van één periode is en n een geheel getal is.
w0= 2p/ T de fundamentele hoekfrequentie.
Door de Fourier stelling, de periodieke functie kan worden geschreven als de volgende som:
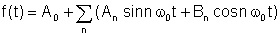
WAAR 
An en Bn de Fourier-coëfficiënten en de som is de Fourier serie.
Een andere vorm, waarschijnlijk iets praktischer:
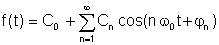
WAAR
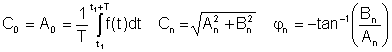
A0 = C0 is de DC of gemiddelde waarde, A1, B1 en C1 zijn de fundamentele componenten en de andere zijn de harmonische termen.
Hoewel er misschien maar een paar termen nodig zijn om sommige golfvormen te benaderen, hebben andere veel termen nodig.
Over het algemeen geldt dat hoe meer termen worden opgenomen, hoe beter de benadering is, maar voor golfvormen die stappen bevatten, zoals rechthoekige impulsen, Gibbs-fenomeen komt in het spel. Naarmate het aantal termen toeneemt, wordt de overschrijding in een steeds kleinere periode geconcentreerd.
An zelfs functie f (t) = f (-t) (symmetrie van de as) vereist alleen cosinustermen.
An rare functie f (t) = - f (-t) (puntsymmetrie) vereist alleen sinusvoorwaarden.
Een golfvorm met spiegel- of halve golfsymmetrie heeft alleen oneven harmonischen in zijn Fourier-weergave.
Hier zullen we niet ingaan op de uitbreiding van de Fourier-serie, maar alleen een gegeven som van sines en cosines gebruiken als excitatie voor een circuit.
In de eerdere hoofdstukken van dit boek hebben we het gehad over sinusoïdale excitatie. Als het circuit lineair is, is de superpositiestelling is geldig. Voor een netwerk met niet-sinusoïdale periodieke excitatie, stelt superpositie ons in staat om bereken de stromen en spanningen van elke Fourier-sinusoïde term één voor één. Wanneer ze allemaal zijn berekend, vatten we tenslotte de harmonische componenten van de respons samen.
Het is een beetje ingewikkeld om de verschillende termen van de periodieke spanningen en stromen te bepalen en in feite kan het een overload aan informatie opleveren. In de praktijk willen we eenvoudig metingen uitvoeren. We kunnen de verschillende harmonische termen meten met a harmonische analyser, spectrumanalysator, golfanalysator of Fourier-analysator. Dit zijn allemaal ingewikkeld en levert waarschijnlijk meer gegevens op dan nodig is. Soms is het voldoende om een periodiek signaal alleen te beschrijven aan de hand van de gemiddelde waarden. Maar er zijn verschillende soorten gemiddelde metingen.
GEMIDDELDE WAARDEN
Eenvoudig gemiddeld or DC term werd in de Fourier-representatie gezien als A0
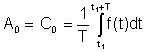
Dit gemiddelde kan gemeten worden met instrumenten zoals de Deprez DC-instrumenten.
Effectieve waarde or rms (root mean square) heeft de volgende definitie:
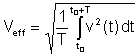
Dit is de belangrijkste gemiddelde waarde omdat de warmteafvoer in weerstanden evenredig is met de effectieve waarde. Veel digitale en sommige analoge voltmeters kunnen de effectieve waarde van spanningen en stromen meten.
Absoluut gemiddelde
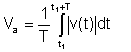
Dit gemiddelde is niet langer belangrijk; eerdere instrumenten maten deze vorm van gemiddelde.
Als we de Fourier-representatie van een spanning of stroomgolfvorm kennen, kunnen we de gemiddelde waarden ook als volgt berekenen:
Eenvoudig gemiddeld or DC term werd in de Fourier-representatie gezien als A0 = C0
Effectieve waarde or rms (root mean square) is, na het integreren van de Fourier-reeks van de spanning:
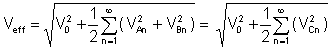
De klirr factor is een zeer belangrijke verhouding van de gemiddelde waarden:
Het is de verhouding van de effectieve waarde van de hogere harmonische termen voor de effectieve waarde van de fundamentele harmonische:
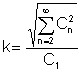
Er lijkt hier een tegenstrijdigheid te zijn: we lossen het netwerk op in termen van harmonische componenten, maar we meten gemiddelde grootheden.
Laten we de methode illustreren aan de hand van eenvoudige voorbeelden:
Voorbeeld 1
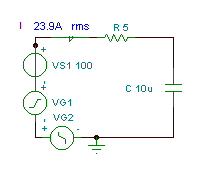
Vind de tijdfunctie en de effectieve (rms) waarde van de spanning vC(T)
als R = 5 ohm, C = 10 mF en v (t) = (100 + 200 cos (w0t) + 30 cos (3 w0t - 90 °)) V, waar de fundamentele hoekfrequentie is w0= 30 krad / s.
Probeer de superpositiestelling te gebruiken om het probleem op te lossen.
De eerste stap is het vinden van de overdrachtsfunctie als functie van de frequentie. Gebruik voor de eenvoud de vervanging: s = j w
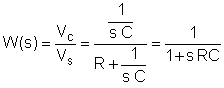
Vervang nu de componentwaarden en s = jk w0waar k = 0; 1; 3 in dit voorbeeld en w0= 30 krad / s. In V, A, ohm, mF en Mrad / s eenheden:
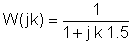
Het is handig om een tabel te gebruiken om de stappen van de numerieke oplossing te ordenen:
k | W (jk) = |
0 |
|
1 |
|
3 |
|
We kunnen de stappen van de superpositie-oplossing samenvatten in een andere tabel. Zoals we al hebben gezien, moeten we, om de complexe piekwaarde van een component te vinden, de complexe piekwaarde van de component van de excitatie vermenigvuldigen met de waarde van de complexe overdrachtsfunctie:
k | V | W | VCk |
0 | 100 | 1 | 100 |
1 | 200 | 0.55e-j56.3° | 110e-j56.3° |
3 | 30e-j90° | 0.217e-j77.5° | 6.51e-j167.5° |
En tot slot kunnen we de tijdfunctie geven met kennis van de complexe piekwaarden van de componenten:
vC(t) = 100 + 110 cos (w0t - 56.3°) + 6.51 cos (3w0t - 167.5°) V
De effectieve waarde van de spanning is:
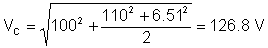
Zoals u kunt zien, meet het meetinstrument van TINA deze effectieve waarde.
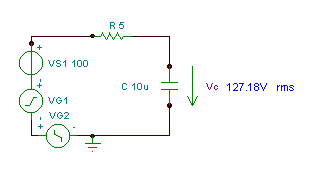
Voorbeeld 2
Zoek de tijdfunctie en de effectieve (rms) waarde van de huidige i (t)
als R = 5 ohm, C = 10 mF en v (t) = (100 + 200 cos (w0t) + 30 cos (3w0t - 90 °)) V waar de fundamentele hoekfrequentie is w0= 30 krad / s.
Probeer het probleem op te lossen met behulp van de superpositiestelling.
 |
De stappen van de oplossing zijn vergelijkbaar met voorbeeld 1, maar de overdrachtsfunctie is anders.
Vervang nu de numerieke waarden en s = jk w0,waar k = 0; 1; 3 in dit voorbeeld.
In V, A, ohm, mF en Mrad / s eenheden:
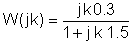
Het is handig om een tabel te gebruiken tijdens de numerieke oplossing:
k | W (jk) = |
0 | |
1 | |
3 | |
We kunnen de stappen van de superpositie in een andere tabel samenvatten. Zoals we al hebben gezien, moeten we, om de piekwaarde van een component te vinden, de complexe piekwaarde van die component van de excitatie vermenigvuldigen met de waarde van de complexe overdrachtsfunctie. Gebruik de complexe piekwaarden van de componenten van de excitatie:
k | VSk | W(Jk) | Ik |
0 | 100 | 0 | 0 |
1 | 200 | 0.162 enj33.7° | 32.4 enj33.7° |
3 | 30 en-j90° | 0.195 enj12.5° | 5.85 en-j77.5° |
En tot slot, als we de complexe piekwaarden van de componenten kennen, kunnen we de tijdfunctie vermelden:
i (t) = 32.4 cos (w0t + 33.7°) + 5.85 cos (3w0t - 77.5°) [EEN]
Tde rms-waarde van de stroom:
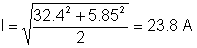
U kunt vaak een gezondheidsonderzoek doen voor een deel van de oplossing. Een condensator kan bijvoorbeeld een gelijkspanning hebben, maar geen gelijkstroom.
Voorbeeld 3
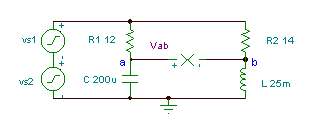
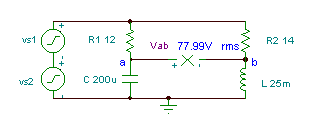
Verkrijg de tijdfunctie van de spanning Vab if R1= 12 ohm, R2 = 14 ohm, L = 25 mH, en
C = 200 mF. De generatorspanning is v (t) = (50 + 80 cos (w0t) + 30 cos (2 w0t + 60 °)) V, waar de grondfrequentie f is0 = 50Hz.
De eerste stap is het vinden van de overdrachtsfunctie:
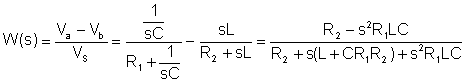
Vervanging van numerieke waarden in V, A, ohm, mH, mF, kHz-eenheden:
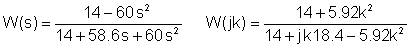
De twee tabellen samenvoegen:
| k V Sk |  | V abk |
|---|---|---|
| 0 50 |  | 50 |
| 1 80 |  | 79.3 en-j66.3 |
| 2 30 ej60 |  | 29.7 en-j44.7 |
Eindelijk de tijdfunctie:
vab(t) = 50 + 79.3 cos (w1t - 66.3°) + 29.7 cos (2w1t - 44.7°) [V]
en de rms-waarde:
English
English
German
French
Spanish
Portuguese
Russian
Chinese (Simplified)
Chinese (Traditional)
Japanese
Korean
Hungarian