Klik of Tik op de onderstaande Voorbeeldcircuits om TINACloud op te roepen en selecteer de interactieve DC-modus om ze online te analyseren.
Klik of Tik op de onderstaande Voorbeeldcircuits om TINACloud op te roepen en selecteer de interactieve DC-modus om ze online te analyseren. Krijg een goedkope toegang tot TINACloud om de voorbeelden te bewerken of om uw eigen circuits te maken
Een sinusvormige spanning kan worden beschreven door de vergelijking:
v (t) = VM sin (ωt + Φ) of v (t) = VM cos (ωt + Φ)
| WAAR | v (t) | Momentele waarde van de spanning, in volt (V). |
| VM | Maximale of piekwaarde van de spanning, in volt (V) | |
| T | Periode: de tijd die nodig is voor één cyclus, in seconden | |
| f | Frequentie - het aantal perioden in 1 seconde, in Hz (Hertz) of 1 / s. f = 1 / T | |
| ω | Hoekfrequentie, uitgedrukt in radialen / s ω = 2 * π * f of ω = 2 * π / T. | |
| Φ | Initiële fase gegeven in radialen of graden. Deze hoeveelheid bepaalt de waarde van de sinus- of cosinusgolf att = 0. | |
| Opmerking: de amplitude van een sinusvormige spanning wordt soms uitgedrukt als VEff, de effectieve of RMS-waarde. Dit heeft te maken met VM volgens de relatie VM= √2VEff, of ongeveer VEff = 0.707 VM |
Hier zijn een paar voorbeelden om de bovenstaande termen te illustreren.
De eigenschappen van de 220 V AC-spanning in huishoudelijke stopcontacten in Europa:
Effectieve waarde: VEff = 220 V
Piekwaarde: VM= √2 * 220 V = 311 V
Frequentie: f = 50 1 / s = 50 Hz
Hoekfrequentie: ω = 2 * π * f = 314 1 / s = 314 rad / s
Periode: T = 1 / f = 20 ms
Tijdfunctie: v (t) = 311 sin (314 t)
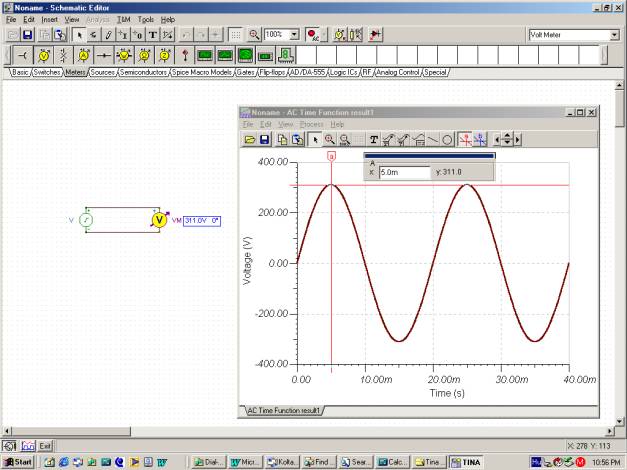
Laten we de tijdfunctie bekijken met behulp van TINA's analyse / AC analyse / tijdfunctie-commando.
U kunt controleren of de periode T = 20m is en die VM = 311 V.
De eigenschappen van de 120 V AC-spanning in het stopcontact in de VS:
Effectieve waarde: VEff = 120 V
Piekwaarde: VM= √2 120 V = 169.68 V ≈ 170 V
Frequentie: f = 60 1 / s = 60 Hz
Hoekfrequentie: ω = 2 * π * f = 376.8 rad / s ≈ 377 rad / s
Periode: T = 1 / f = 16.7 ms
Tijdfunctie: v (t) = 170 sin (377 t)
Merk op dat in dit geval de tijdfunctie kan worden gegeven als v (t) = 311 sin (314 t + Φ) of v (t) = 311 cos (314 t + Φ), omdat in het geval van de uitgangsspanning we weet niet de beginfase.
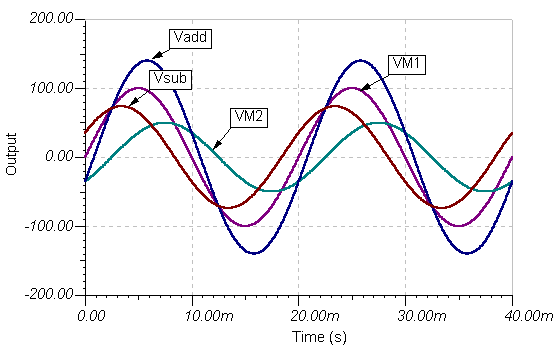
De beginfase speelt een belangrijke rol wanneer meerdere spanningen tegelijkertijd aanwezig zijn. Een goed praktisch voorbeeld is het driefasensysteem, waarbij drie spanningen van dezelfde piekwaarde, vorm en frequentie aanwezig zijn, die elk een 120 ° faseverschuiving ten opzichte van de andere hebben. In een 60 Hz-netwerk zijn de tijdfuncties:
vA(t) = 170 sin (377 t)
vB(t) = 170 zonde (377 t - 120 °)
vC(t) = 170 sin (377 t + 120 °)
De volgende afbeelding gemaakt met TINA toont het circuit met deze tijdfuncties als de spanningsgeneratoren van TINA.
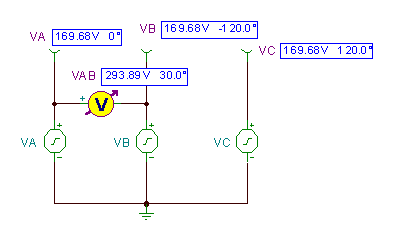

Het spanningsverschil vAB= vA(t) - vB(t) wordt getoond als opgelost door TINA's analyse / AC analyse / tijdfunctie-commando.
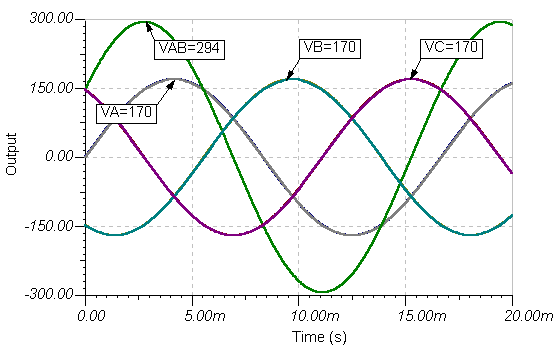

Merk op dat de top van vAB (t) is ongeveer 294 V, groter dan de 170 V-pieken van de vA(t) of vB(t) spanningen, maar ook niet eenvoudigweg de som van hun piekspanningen. Dit komt door het faseverschil. We zullen bespreken hoe de resulterende spanning (dat is Ö3 * 170 @ 294 in dit geval) later in dit hoofdstuk en ook in het afzonderlijke hoofdstuk Driefasige systemen hoofdstuk.
Kenmerkende waarden van sinusoïdale signalen
Hoewel een wisselstroomsignaal continu varieert tijdens zijn periode, is het eenvoudig om enkele kenmerkende waarden te definiëren voor het vergelijken van de ene golf met een andere: dit zijn de piek-, gemiddelde- en roermiddelkwadraten (rms).
We hebben de piekwaarde al bereikt VM , dat is gewoon de maximale waarde van de tijdfunctie, de amplitude van de sinusoïdale golf.
Soms wordt de piek-tot-piek (pp) -waarde gebruikt. Voor sinusvormige spanningen en stromen is de piek-tot-piekwaarde het dubbele van de piekwaarde.
De gemiddelde waarde van de sinusgolf is het rekenkundig gemiddelde van de waarden voor de positieve halve cyclus. Het wordt ook genoemd absoluut gemiddelde omdat het hetzelfde is als het gemiddelde van de absolute waarde van de golfvorm. In de praktijk komen we deze golfvorm tegen rectificeren de sinusgolf met een circuit dat een volledige golfgelijkrichter wordt genoemd.
Er kan worden aangetoond dat het absolute gemiddelde van een sinusoïdale golf is:
VAV= 2 / π VM ≅ 0.637 VM
Merk op dat het gemiddelde van een hele cyclus nul is.
De rms of effectieve waarde van een sinusvormige spanning of stroom komt overeen met de equivalente DC-waarde die hetzelfde verwarmingsvermogen produceert. Een spanning met een effectieve waarde van 120 V produceert bijvoorbeeld hetzelfde verwarmings- en verlichtingsvermogen in een lamp als 120 V van een gelijkstroomspanningsbron. Er kan worden aangetoond dat de rms of effectieve waarde van een sinusoïdale golf is:

Vrms = VM / √2 ≅ 0.707 VM
Deze waarden kunnen op dezelfde manier worden berekend voor zowel spanningen als stroom.
De effectieve waarde is in de praktijk erg belangrijk. Tenzij anders aangegeven, worden wisselstroomspanningen (bijv. 110V of 220V) gegeven in rms-waarden. De meeste AC-meters zijn gekalibreerd in rms en geven het rms-niveau aan.
Voorbeeld 1 Zoek de piekwaarde van de sinusvormige spanning in een elektrisch netwerk met 220 V rms-waarde.
VM = 220 / 0.707 = 311.17 V
Voorbeeld 2 Zoek de piekwaarde van de sinusvormige spanning in een elektrisch netwerk met 110 V rms-waarde.
VM = 110 / 0.707 = 155.58 V
Voorbeeld 3 Zoek het (absolute) gemiddelde van de sinusoïdale spanning als de rms-waarde 220 V is.
Va = 0.637 * VM = 0.637 * 311.17 = 198.26 V
Voorbeeld 4 Zoek het absolute gemiddelde van de sinusvormige spanning als de rms-waarde 110 V is.
De piek van de spanning van Voorbeeld 2 is155.58 V en daarom:
Va = 0.637 * VM = 0.637 * 155.58 = 99.13 V
Voorbeeld 5 Zoek de verhouding tussen het absolute gemiddelde (Va) en rms (V) -waarden voor de sinusoïdale golfvorm.
V / Va = 0.707 / 0.637 = 1.11
Merk op dat u geen gemiddelde waarden in een AC-circuit kunt toevoegen omdat dit tot onjuiste resultaten leidt.
phasors
Zoals we in de vorige paragraaf al hebben gezien, is het vaak nodig om in AC-circuits sinusvormige spanningen en stromen met dezelfde frequentie toe te voegen. Hoewel het mogelijk is om de signalen numeriek toe te voegen met TINA, of door trigonometrische relaties te gebruiken, is het handiger om de zogenaamde trigonometrische relaties te gebruiken. fasor methode. Een fasor is een complex getal dat de amplitude en fase van een sinusvormig signaal vertegenwoordigt. Het is belangrijk op te merken dat de phasor niet de frequentie vertegenwoordigt, die voor alle fasers hetzelfde moet zijn.
Een fasor kan worden behandeld als een complex getal of grafisch worden weergegeven als een vlakke pijl in het complexe vlak. De grafische weergave wordt een fasordiagram genoemd. Met behulp van phasordiagrammen kunt u fasors in een complex vlak optellen of aftrekken met de driehoek- of parallellogramregel.
Er zijn twee vormen van complexe getallen: rechthoekig en polair.
De rechthoekige weergave bevindt zich in de forma + jb, waar j = Ö-1 is de denkbeeldige eenheid.
De polaire weergave heeft de vorm Aej j , waarbij A de absolute waarde (amplitude) en f is de hoek van de phasor van de positieve reële as, in de richting tegen de wijzers van de klok in.
We zullen gebruiken pin letters voor complexe hoeveelheden.
Laten we nu eens kijken hoe de corresponderende fasor afgeleid kan worden van een tijdfunctie.
Stel eerst dat alle spanningen in het circuit worden uitgedrukt in de vorm van cosinusfuncties. (Alle voltages kunnen naar dat formulier worden geconverteerd.) Vervolgens de fasor overeenkomend met de spanning van v (t) = VM cos ( w t+f) is: VM = VMe jf , die ook de complexe piekwaarde wordt genoemd.
Beschouw bijvoorbeeld de spanning: v (t) = 10 cos ( w t + 30°)
De bijbehorende phasor is: 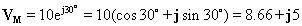
We kunnen de tijdfunctie van een phasor op dezelfde manier berekenen. Eerst schrijven we de phasor in polaire vorm, bijvoorbeeld VM = VMe jr en dan is de bijbehorende tijdfunctie
v (t) = VM (Cos (wt+r).
Bekijk bijvoorbeeld de phasor VM = 10 - j20 V
Breng het in polaire vorm:
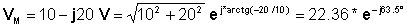
En daarom is de tijdfunctie: v (t) = 22.36 cos (wt - 63.5°) V
Phasors worden vaak gebruikt om de complexe effectieve of effectieve waarde van de spanningen en stromen in wisselstroomcircuits te definiëren. Gegeven v (t) = VMcos (wt+r) = 10cos (wt + 30°)
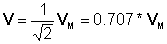
Numeriek:
v (t) = 10 * cos (wt-30°)
De complexe effectieve (rms) waarde: V = 0.707 * 10 * e- j30° = 7.07 e- j30° = 6.13 - j 3.535
Vice versa: als de complexe effectieve waarde van een spanning is:
V = - 10 + j 20 = 22.36 e j 116.5°
dan de complexe piekwaarde: 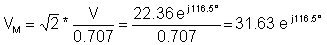
en de tijdfunctie: v (t) = 31.63 cos ( wt + 116.5° ) V
Een korte rechtvaardiging van de bovenstaande technieken is als volgt. Gegeven een tijdfunctie
VM (Cos ( w t+r), laten we het definiëren complexe tijdfunctie als:
v (t) = VM e jr e jwt = VMe jwt = VM (Cos (r) + j zonde(r)) E jwt
WAAR VM =VM e j r t = VM (Cos (r) + j zonde(r)) is alleen de hierboven geïntroduceerde phasor.
Bijvoorbeeld, de complexe tijdfunctie van v (t) = 10 cos (wt + 30°)
v (t) = VMe jwt = 10 e j30 e jwt = 10e jwt (cos (30) + j sin (30)) = e jwt (8.66 +j5)
Door de complexe tijdfunctie in te voeren, hebben we een representatie met zowel een reëel deel als een imaginair deel. We kunnen altijd de oorspronkelijke echte functie van tijd herstellen door het echte deel van ons resultaat te nemen: v (t) = Re {v(T)}
De complexe tijdfunctie heeft echter het grote voordeel dat, aangezien alle complexe tijdfuncties in de beschouwde wisselstroomschakelingen dezelfde e hebbenjwt vermenigvuldiger, kunnen we dit uitrekenen en gewoon met de fasers werken. Bovendien gebruiken we in de praktijk de ejwt helemaal geen deel - alleen de transformaties van de tijdfuncties naar de fasors en terug.
Laten we het volgende voorbeeld bekijken om het voordeel van het gebruik van phasors te demonstreren.
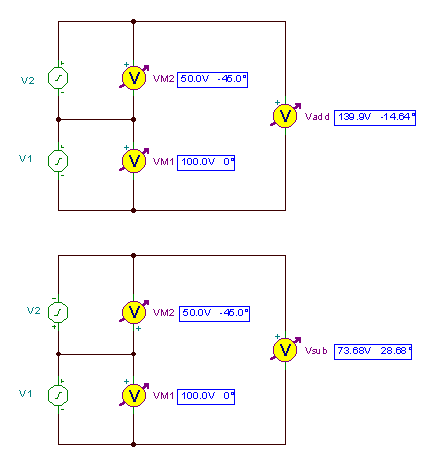
Voorbeeld 6 Zoek de som en het verschil van de spanningen:
v1 = 100 cos (314 * t) en v2 = 50 cos (314 * t-45°)
Noteer eerst de fasors van beide spanningen:
V1M = 100 V2M= 50 e - j 45° = 35.53 - j 35.35
Vandaar:
Vtoevoegen = V1M + V2M = 135.35 - j 35.35 = 139.89 e- j 14.63°
Vbeneden = V1M - V2M = 64.65 + j35.35 = 73.68 en j 28.67°
en dan de tijdfuncties:
vtoevoegen(t) = 139.89 * cos (wt - 14.63°)
vbeneden(t) = 73.68 * cos (wt + 28.67°)
Zoals dit eenvoudige voorbeeld laat zien, is de methode van phasors.is een extreem krachtige tool voor het oplossen van AC-problemen.
Laten we het probleem oplossen met de tools in de interpreter van TINA.
{berekening van v1 + v2}
v1: = 100
v2: = 50 * exp (-pi / 4 * j)
v2 = [-35.3553 35.3553 * j]
v1add: = v1 + v2
v1add = [-135.3553 35.3553 * j]
abs (v1add) = [139.8966]
radtodeg (arc (v1add)) = [- 14.6388]
{berekening van v1-v2}
v1sub: = v1-v2
v1sub = [64.6447 35.3553 * + j]
abs (v1sub) = [73.6813]
radtodeg (arc (v1sub)) = [28.6751]
#berekening van v1+v2
importeer wiskunde als m
importeer cmath als c
v1=100
v2=50*c.exp(complex(0,-c.pi/4))
afdrukken(“v2=”,v2)
vadd=v1+v2
print(“vadd=”,vadd)
print(“abs(vadd)=”,abs(vadd))
print(“graden(boog(vadd))=”,m.graden(c.fase(vadd)))
#berekening van v1-v2
vsub=v1-v2
print(“vsub=”,vsub)
print(“abs(vsub)=”,abs(vsub))
print(“graden(boog(vsub))=”,m.graden(c.fase(vsub)))
De amplitude- en fase-resultaten bevestigen de handberekeningen.
Laten we nu het resultaat controleren met behulp van de AC-analyse van TINA.
Voordat we de analyse uitvoeren, zorgen we ervoor dat de Basisfunctie voor AC ik ben ingesteld op cosinus in de Editor-opties dialoogvenster in het menu Beeld / Optie. We zullen de rol van deze parameter uitleggen op Voorbeeld 8.
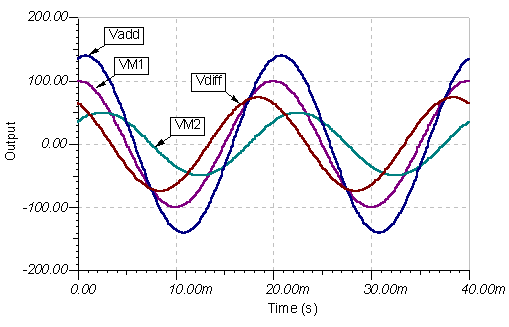
De circuits en de resultaten:
Nogmaals, het resultaat is hetzelfde. Dit zijn de tijdfunctie grafieken:
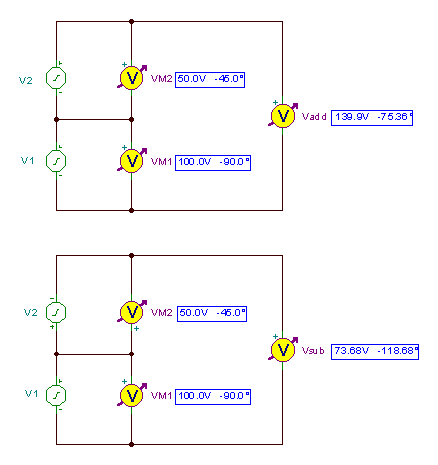
Voorbeeld 7 Zoek de som en het verschil van de spanningen:
v1 = 100 sin (314 * t) en v2 = 50 cos (314 * t-45°)
Dit voorbeeld roept een nieuwe vraag op. Tot nu toe hebben we vereist dat alle tijdfuncties worden gegeven als cosinusfuncties. Wat zullen we doen met een tijdfunctie gegeven als een sinus? De oplossing is om de sinusfunctie te transformeren naar een cosinusfunctie. Gebruik de trigonometrische relatie sin (x) = cos (x-p/ 2) = cos (x-90°), ons voorbeeld kan als volgt worden geherformuleerd:
v1 = 100 cos (314t - 90°) en v2 = 50 cos (314 * t - 45°)
Nu zijn de fasors van de spanningen:
V1M = 100 e - j 90° = -100 j V2M= 50 e - j 45° = 35.53 - j 35.35
Vandaar:
V toevoegen = V1M + V2M = 35.53 - j 135.35
V beneden = V1M - V2M = - 35.53 - j 64.47
en dan de tijdfuncties:
vtoevoegen(t) = 139.8966 cos (wt-75.36°)
vbeneden(t) = 73.68 cos (wt-118.68°)
Laten we het probleem oplossen met de tools in de interpreter van TINA.
{berekening van v1 + v2}
v1: = - * j 100
v2: = 50 * exp (-pi / 4 * j)
v2 = [35.3553 - 35.3553 * j]
v1add: = v1 + v2
v1add = [-35.3553 135.3553 * j]
abs (v1add) = [139.8966]
radtodeg (arc (v1add)) = [- 75.3612]
{berekening van v1-v2}
v1sub: = v1-v2
v1sub = [- 35.3553 - 64.6447 * j]
abs (v1sub) = [73.6813]
radtodeg (arc (v1sub)) = [- 118.6751]
#berekening van v1+v2
importeer wiskunde als m
importeer cmath als c
v1=100
v2=50*c.exp(complex(0,-c.pi/4))
afdrukken(“v2=”,v2)
vadd=v1+v2
print(“vadd=”,vadd)
print(“abs(vadd)=”,abs(vadd))
print(“graden(boog(vadd))=”,m.graden(c.fase(vadd)))
#berekening van v1-v2
vsub=v1-v2
print(“vsub=”,vsub)
print(“abs(vsub)=”,abs(vsub))
print(“graden(boog(vsub))=”,m.graden(c.fase(vsub)))
Laten we het resultaat controleren met de AC-analyse van TINA
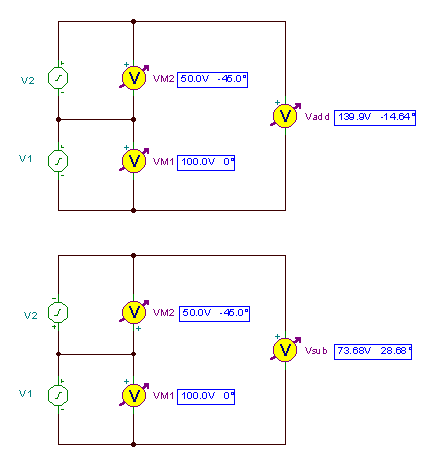
Voorbeeld 8
Zoek de som en het verschil van de spanningen:v1 = 100 sin (314 * t) en v2 = 50 sin (314 * t-45°)
Dit voorbeeld roept nog een probleem op. Wat als alle voltages worden gegeven als sinusgolven en we willen ook het resultaat zien als een sinusgolf ?. We zouden natuurlijk beide spanningen kunnen omzetten naar cosinusfuncties, het antwoord kunnen berekenen en dan het resultaat terug kunnen converteren naar een sinusfunctie - maar dit is niet nodig. We kunnen fasoren creëren uit de sinusgolven op dezelfde manier als we deden uit cosinusgolven en dan gewoon hun amplitude en fasen gebruiken als amplitude en fase van sinusgolven in het resultaat.
Dit zal uiteraard hetzelfde resultaat geven als het transformeren van de sinusgolven naar cosinusgolven. Zoals we in het vorige voorbeeld zagen, is dit gelijk aan vermenigvuldigen met -j en dan cos (x) = sin (x-90°) relatie om het terug te transformeren naar een sinusgolf. Dit komt overeen met vermenigvuldigen met j. Met andere woorden, omdat -j × j = 1, we kunnen de fasors gebruiken die rechtstreeks zijn afgeleid van de amplituden en fasen van sinusgolven om de functie weer te geven en er vervolgens rechtstreeks naar terugkeren. Ook op dezelfde manier redenerend over de complexe tijdfuncties kunnen we sinusgolven beschouwen als de imaginaire delen van de complexe tijdfuncties en ze aanvullen met de cosinusfunctie om de volledige complexe tijdfunctie te creëren.
Laten we de oplossing voor dit voorbeeld bekijken met behulp van de sinusfuncties als de basis van de fasors (transformeren van sin ( w t) naar de echte eenheidfasor (1)).
V1M = 100 V2M= 50 e - j 45° = 35.53 - j 35.35
Vandaar:
V toevoegen = V1M + V2M = 135.53 - j 35.35
V beneden = V1M - V2M = 64.47+ j 35.35
Merk op dat de phasors exact hetzelfde zijn als in Voorbeeld 6 maar niet de tijdfuncties:
v3(t) = 139.9sin (wt - 14.64°)
v4(t) = 73.68sin (wt + 28.68°)
Zoals u kunt zien, is het heel gemakkelijk om het resultaat te verkrijgen met behulp van sinusfuncties, vooral wanneer onze initiële gegevens sinusgolven zijn. Veel studieboeken geven er de voorkeur aan om de sinusgolf te gebruiken als de basisfunctie van fasoren. In de praktijk kunt u beide methoden gebruiken, maar verwar ze niet.
Wanneer u de phasors maakt, is het erg belangrijk dat alle tijdfuncties eerst worden geconverteerd naar sinus of cosinus. Als u vanuit sinusfuncties bent begonnen, moeten uw oplossingen worden weergegeven met sinusfuncties wanneer fasers terugkeren naar tijdfuncties. Hetzelfde geldt als u begint met cosinusfuncties.
Laten we hetzelfde probleem oplossen met de interactieve modus van TINA. Omdat we sinusfuncties als basis voor het maken van de phasors willen gebruiken, moet u ervoor zorgen dat de Basisfunctie voor AC is ingesteld op hun in de Editor-opties dialoogvenster in het menu Beeld / Optie.

De circuits voor het maken van de som en het verschil van de golfvormen en het resultaat:
en de tijdfuncties: