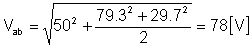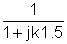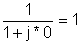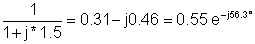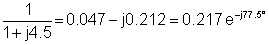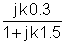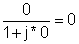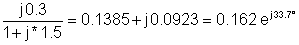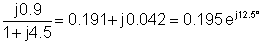Faceți clic sau atingeți exemplele de mai jos pentru a invoca TINACloud și selectați modul Interactiv DC pentru a le analiza online. Obțineți acces la un cost redus la TINACloud pentru a edita exemplele sau pentru a crea propriile circuite
Teorema Fourier afirmă că orice formă de undă periodică poate fi sintetizată adăugând termeni sinusoidali și cosinici ponderați corespunzător de diferite frecvențe. Teorema este bine acoperită în alte manuale, așa că vom rezuma doar rezultatele și vom arăta câteva exemple.
Fie funcția noastră periodică să fie f (t) = f (t ±nT) unde T este timpul unei perioade și n este un număr întreg.
w0= 2p/ T frecvența unghiulară fundamentală.
Langa Teorema lui Fourier, funcția periodică poate fi scrisă ca următoarea sumă:
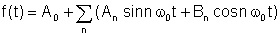
Unde 
An și Bn sunt Coeficienții Fourier iar suma este Seria Fourier.
O altă formă, probabil un pic mai practică:
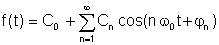
Unde
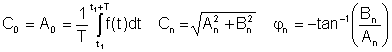
A0 = C0 este valoarea DC sau media, A1, B1 și C1 sunt componentele fundamentale, iar ceilalți sunt termenii armonici.
În timp ce doar câțiva termeni pot fi necesari pentru a aproxima unele forme de undă, alții vor necesita mulți termeni.
În general, cu cât sunt incluși mai mulți termeni, cu atât este mai bună aproximarea, dar pentru formele de undă care conțin pași, cum ar fi impulsurile dreptunghiulare, Fenomenul Gibbs intră în joc. Pe măsură ce numărul de termeni crește, depășirea excesivă devine concentrată într-o perioadă de timp tot mai mică.
An chiar și funcția f (t) = f (-t) (simetria axei) necesită doar termeni cosinici.
An ciudat f (t) = - f (-t) (simetrie punctuală) necesită numai termeni sinusoidali.
O formă de undă cu oglindă sau simetrie de jumătate de undă are doar ciudat armonice în reprezentarea sa Fourier.
Aici nu ne vom ocupa de expansiunea seriei Fourier, ci vom folosi doar o sumă dată de sinusuri și cosinus ca o excitație pentru un circuit.
În capitolele anterioare ale acestei cărți, am tratat excitația sinusoidală. Dacă circuitul este liniar, teorema superpozitiei este valabil. Pentru o rețea cu excitație periodică nonsonoidală, suprapunerea ne permite calculați curenții și tensiunile datorate fiecărui termen sinusoid Fourier unul câte unul. Când toate sunt calculate, vom rezuma în cele din urmă la componentele armonice ale răspunsului.
Este un pic complicat să determinăm diferiții termeni ai tensiunilor și curenților periodici și, de fapt, poate genera o suprasarcină de informații. În practică, am dori să facem pur și simplu măsurători. Putem măsura diferiții termeni armonici folosind a analizor armonic, analizor de spectru, analizor de unde sau analizor Fourier. Toate astea sunt complicat și, probabil, obține mai multe date decât este necesar. Uneori este suficient să descriem un semnal periodic numai prin valorile sale medii. Există însă mai multe tipuri de măsurători medii.
IN MEDIE VALORI
Media simplă or DC termenul a fost văzut în reprezentarea Fourier ca A0
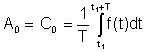
Această medie poate fi măsurată cu instrumente precum Deprez Instrumente cu curent continuu
Valoare efectivă or rms (rădăcina medie pătrată) are următoarea definiție:
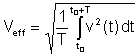
Aceasta este cea mai importantă valoare medie, deoarece căldura disipată în rezistențe este proporțională cu valoarea efectivă. Multe voltmetre digitale și unele analogice pot măsura valoarea efectivă a tensiunilor și a curenților.
Media absolută
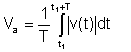
Această medie nu mai este importantă; instrumentele anterioare au măsurat această formă de medie.
Dacă cunoaștem reprezentarea Fourier a unei tensiuni sau a unei forme de undă de curent, putem calcula, de asemenea, valorile medii după cum urmează:
Media simplă or DC termenul a fost văzut în reprezentarea Fourier ca A0 = C0
Valoare efectivă or rms (media pătrat rădăcină) este, după integrarea seriei Fourier a tensiunii:
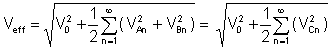
factorul klirr este un raport foarte important dintre valorile medii:
Este raportul dintre valoarea efectivă a termenilor armonici superiori la valoarea efectivă a armonicii fundamentale:
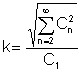
Se pare că există o contradicție aici - rezolvăm rețeaua în termeni de componente armonice, dar măsurăm cantități medii.
Să ilustrăm metoda prin exemple simple:
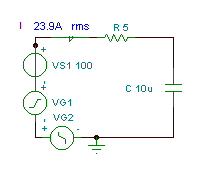
Exemplu 1
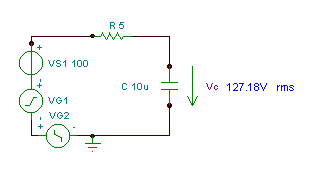
Găsiți funcția timp și valoarea efectivă (rms) a tensiunii vC(T)
dacă R = 5 ohm, C = 10 mF și v (t) = (100 + 200 cos (w0t) + 30 cos (3 w0t - 90 °)) V, unde este frecvența unghiulară fundamentală w0= 30 krad / s.
Încercați să utilizați teorema superpoziției pentru a rezolva problema.
Primul pas este găsirea funcției de transfer în funcție de frecvență. Pentru simplitate, utilizați substituția: s = j w
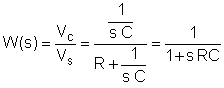
Acum înlocuiți valorile componente și s = jk w0unde k = 0; 1; 3 în acest exemplu și w0= 30 krad / s. În V, A, ohm, mF și Mrad:
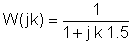
Este util să folosiți un tabel pentru a organiza pașii soluției numerice:
k | W (jk) = |
0 |
|
1 |
|
3 |
|
Putem rezuma pașii soluției de superpoziție într-un alt tabel. Așa cum am văzut deja, pentru a găsi valoarea maximă complexă a unei componente, ar trebui să înmulțim valoarea de vârf complexă a componentei excitației cu valoarea funcției de transfer complex:
k | V | W | VCk |
0 | 100 | 1 | 100 |
1 | 200 | 0.55e-j56.3° | 110e-j56.3° |
3 | 30e-j90° | 0.217e-j77.5° | 6.51e-j167.5° |
Și, în sfârșit, putem oferi funcției timp cunoscând valorile de vârf complexe ale componentelor:
vC(t) = 100 + 110 cos (w0t - 56.3°) + 6.51 cos (3w0t - 167.5°) V
Valoarea rms (efectivă) a tensiunii este:
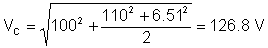
După cum puteți vedea, instrumentul de măsurare TINA măsoară această valoare RMS.
Exemplu 2
Găsiți funcția timp și valoarea efectivă (rms) a curentului i (t)
dacă R = 5 ohm, C = 10 mF și v (t) = (100 + 200 cos (w0t) + 30 cos (3w0t - 90 °)) V unde este frecvența unghiulară fundamentală w0= 30 krad / s.
Încercați să rezolvați problema folosind teorema superpoziției.
 |
Etapele soluției sunt similare cu exemplul 1, dar funcția de transfer este diferită.
Acum înlocuiți valorile numerice și s = jk w0,unde k = 0; 1; 3 în acest exemplu.
În V, A, ohm, mF și Mrad:
Este util să utilizați un tabel în timpul soluției numerice:
k | W (jk) = |
0 | |
1 | |
3 | |
Putem rezuma pașii superpoziției într-un alt tabel. După cum am văzut deja, pentru a găsi valoarea de vârf a unei componente, ar trebui să înmulțim valoarea de vârf complexă a acelei componente a excitației cu valoarea funcției de transfer complex. Utilizați valorile de vârf complexe ale componentelor excitației:
k | VSk | W(Jk) | Ik |
0 | 100 | 0 | 0 |
1 | 200 | 0.162 ej33.7° | 32.4 ej33.7° |
3 | 30 e-j90° | 0.195 ej12.5° | 5.85 e-j77.5° |
Și în final, cunoscând valorile de vârf complexe ale componentelor, putem afirma funcția de timp:
i (t) = 32.4 cos (w0t + 33.7°) + 5.85 cos (3w0t - 77.5°) [A]
Tel valorează valoarea curentului:
Adesea puteți face o verificare a sănătății pentru o parte din soluție. De exemplu, un condensator poate avea o tensiune continuă, dar nu un curent continuu.
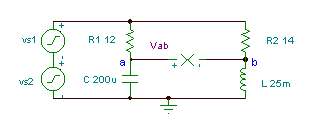
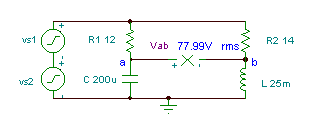
Exemplu 3
Obțineți funcția de timp a tensiunii Vab if R1= 12 ohm, R2 = 14 ohmi, L = 25 mH și
C = 200 mF. Tensiunea generatorului este v (t) = (50 + 80 cos (w0t) + 30 cos (2 w0t + 60 °)) V, unde frecvența fundamentală este f0 = 50 Hz.
Primul pas este să găsiți funcția de transfer:
Înlocuirea valorilor numerice în unitățile V, A, ohm, mH, mF, kHz:
Îmbinarea celor două mese:
| k V Sk |  | V ABK |
|---|---|---|
| 0 50 |  | 50 |
| 1 80 |  | 79.3 e-j66.3 |
| 2 30 ej60 |  | 29.7 e-j44.7 |
În cele din urmă funcția de timp:
vab(t) = 50 + 79.3 cos (w1t - 66.3°) + 29.7 cos (2w1t - 44.7°) [V]
și valoarea rms:
English
English
German
French
Spanish
Portuguese
Russian
Chinese (Simplified)
Chinese (Traditional)
Japanese
Korean
Hungarian