 Lai izmantotu TINACloud un atlasītu interaktīvo līdzstrāvas režīmu, lai analizētu tos tiešsaistē, noklikšķiniet uz zemāk esošās piemēru shēmas vai pieskarieties tam.
Lai izmantotu TINACloud un atlasītu interaktīvo līdzstrāvas režīmu, lai analizētu tos tiešsaistē, noklikšķiniet uz zemāk esošās piemēru shēmas vai pieskarieties tam. Iegūstiet zemu izmaksu piekļuvi TINACloud, lai rediģētu piemērus vai izveidotu savas shēmas
Šajā un turpmākajās nodaļās mēs iepazīstināsim ar ļoti svarīgu tēmu: AC vai maiņstrāvu. Mainīgās strāvas nosaukums nav ļoti precīzs un parasti aptver ķēdes ar sinusoidāliem spriegumiem un strāvām; tomēr mainīgā strāva var nozīmēt arī jebkuru patvaļīgu strāvas viļņu formu. AC sprieguma nozīme ir tāda, ka šāda veida spriegums tiek izmantots galvenajam elektroenerģijas avotam mājās un rūpniecībā visā pasaulē. Tas ir arī pamats daudziem elektronikas, telekomunikāciju un rūpniecības lietojumiem.
Lai apstrādātu sinusoidālās viļņu formas un ar tām saistītās shēmas, mēs izmantosim vienkāršu un elegantu metodi, ko sauc par fāzoru metodi. Fasori balstās uz komplekso numuru īpašībām, kas ir ideāli piemērotas sinusoidālu daudzumu attēlošanai. Šajā nodaļā mēs apkoposim galvenos faktus par sarežģītiem numuriem un to darbību. Mēs arī parādīsim, kā TINA tulks ļauj viegli veikt aprēķinus ar sarežģītiem numuriem.
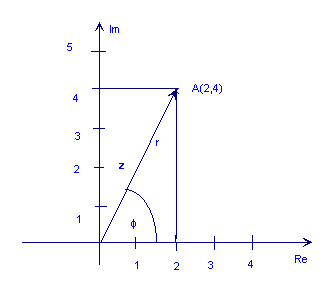
Sarežģītie numuri sastāv no divām daļām: a īsta daļa (x), kas ir reāls skaitlis, un tā saucamais iedomātā daļa (y), kas ir reālais skaitlis, kas reizināts ar 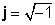
z = x + jy
kur 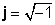
Sarežģītu numuru piemēri:
z 1 = 1 + j
z 2 = 4-2 j
z 3 = 3- 5j
Kompleksie skaitļi sākotnēji tika ieviesti septiņpadsmitajā gadsimtā, lai attēlotu polinomu saknes, kuras nevarēja attēlot tikai ar reāliem skaitļiem. Piemēram, vienādojuma x saknes2 + 2x + 2 = 0 var raksturot tikai kā 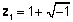
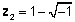
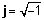
Komplekso numuru ģeometriskais attēlojums
Taisnstūra forma
Tā kā sarežģītu skaitli vienmēr var iedalīt tā reālajās un sarežģītajās daļās, mēs komplekso skaitli varam attēlot kā punktu divdimensiju plaknē. Kompleksa skaitļa reālā daļa ir punkta projekcija uz reālo asi, un skaitļa iedomātā daļa ir projekcija uz iedomāto asi. Kad sarežģīts skaitlis tiek attēlots kā reālo un iedomāto daļu summa, mēs sakām, ka tas ir iekšā taisnstūra or algebriskā forma.
Nākamajā attēlā redzams kompleksā numurs z = 2 + 4j
Polārā un eksponenciālā forma
Kā redzams no attēla iepriekš, punktu A varētu attēlot arī ar bultiņas garumu, r (ko sauc arī par absolūto vērtību, lielumu vai amplitūdu) un tā leņķi (vai fāzi), φ attiecībā pret pozitīvo horizontālo asi pretēji pulksteņrādītāja virzienam. Tas ir polārs kompleksa skaitļa forma. To apzīmē kā r ∠ φ.
Nākamais solis ir ļoti svarīgs. Var ierakstīt arī kompleksa numuru polārajā formā eksponenciāli forma:
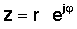
Šis vienkāršais izteiciens ir atšķirīgs ar to, ka eksponendā tam ir iedomāts skaitlis, nevis parastais reālais skaitlis. Šis sarežģītais eksponenciālais uzvedība atšķiras no eksponenciālās funkcijas ar reālu argumentu. Kamēr ex strauji pieaug, palielinoties x> 0, un samazinās, ja funkcija x <0, funkcija 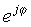
Eulera formula nodrošina vienotu saikni starp komplekso numuru taisnstūra, polārajiem un eksponenciālajiem veidiem:
z = x + jy = re jφ = r (cos φ + j grēks φ )
kur 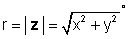
un φ = iedegums-1 (y / x).
Mūsu iepriekš minētais piemērs z = 2 + 4j:
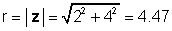
φ = iedegums-1 (4 / 2) = 63.4 °
tāpēc 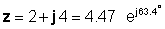
Vai otrādi:
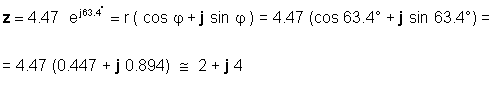
Jums būs jābūt prasmīgam abās veidlapās, atkarībā no lietojuma. Piemēram, saskaitīšanu vai atņemšanu acīmredzami ir vieglāk izdarīt, ja skaitļi ir taisnstūra formā, savukārt reizināšanu un dalīšanu ir vieglāk izdarīt, ja skaitļi ir eksponenciālā formā.
Darbības ar sarežģītiem numuriem
Darbības, kuras var veikt ar sarežģītiem skaitļiem, ir līdzīgas reālajiem skaitļiem. Noteikumi un dažas jaunas definīcijas ir apkopotas turpmāk.
Darbības ar j
Operācijas ar j vienkārši sekojiet iedomātās vienības definīcijai,


Lai varētu strādāt ātri un precīzi, šie noteikumi ir jāatceras:
j 2 = -1
j 3 =-j
j 4 =1
1/j = -j
j2 = -1 vienkārši izriet no definīcijas 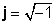
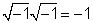
1 /j, mēs reizinām 1 /jby j / j = 1 un saņemiet j/ (jj) = j / (- 1) = -j.
Komplekss konjugāts
Kompleksā kompleksa konjugāts ir viegli iegūstams un ir diezgan svarīgs. Lai iegūtu kompleksā skaitļa komplekso konjugātu taisnstūra formā, vienkārši nomainiet iedomātās daļas zīmi. Lai to izdarītu skaitam eksponenciālā formā, mainiet kompleksā numura leņķa zīmi, saglabājot tā absolūtu vērtību.
Kompleksā kompleksa konjugāts z bieži apzīmē ar z*.
Ņemot vērā kompleksa numuru z= a + jb, tā komplekss konjugāts ir z*= a– jb.
If z tiek dota eksponenciālā formā, 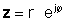
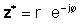
Izmantojot iepriekš minētās definīcijas, ir viegli redzēt, ka komplekss skaitlis, kas reizināts ar tās komplekso konjugātu, dod kompleksā numura absolūtās vērtības kvadrātu:
zz* = r2 = a2 + b2
Turklāt, pievienojot vai atņemot jebkuru komplekso numuru un tā konjugātu, mēs iegūstam šādas attiecības:
z + z * = 2a
tāpēc
Re (z) = a = ( z + z * ) / 2
Līdzīgi:
z - z * =j2b
tāpēc
ES esmu(z) = b = ( z -z * ) / 2j
Pierādījums:
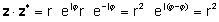
reālās un iedomātās daļas reizināšana un izmantošana j2= -1
zz* = (a + jba - jb) = a2+a jba jb - jbjb = a2j2 = a2 + b2
z + z* = a + jb + a - jb = 2a
z - z*= a + jb - a + jb =j2b
Skaitliskie piemēri:
Taisnstūra formā:
z = 3 + j4
z* = 3– j4
zz * = 9 + 16 = 25
Polārā formā
z = 5 = 53.13 °
z * = 5 ~ 53.13 °
Eksponenciālā veidā:
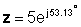
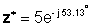
Saskaitīšana un atņemšana
Kompleksu skaitļu saskaitīšana un atņemšana ir vienkārša - mums reālā un iedomātā daļa jāpievieno tikai atsevišķi. Piemēram, ja
z1 = 3 - 4j un z2 = 2 + 3j
tAD
z1 + z2 = 3 - 4j + 2 + 3j = 3 + 2 - 4j + 3j = 5 - j
z1 - z2 = 3 - 4j - 2 - 3j = 3 - 2 - 4j - 3j = 1 - j7
Acīmredzot šīm operācijām mums vajadzētu izmantot taisnstūra formu. Ja skaitļi tiek doti eksponenciālā vai polārā formā, mums tie vispirms jāpārveido taisnstūra formā, izmantojot Eulera formulu, kā norādīts iepriekš.
Reizināšana
Komplekso skaitļu reizināšanai ir divas metodes -
Sarežģītu skaitļu reizinājums, kas dots taisnstūra formā
Lai veiktu operāciju, vienkārši reiziniet viena numura reālo un iedomāto daļu ar otra numura reālo un iedomāto daļu un izmantojiet identitāti j2 = -1.
z1z2 = (a1 + jb1) (a2 + jb2) = a1 a2 + jb1a2+ jb2a1 - b1b2 = a1 a2- b1b2 + j(b1a2+ jb2a1)
Ja kompleksa numuri ir norādīti skaitliski, iepriekšminētā formula nav jāizmanto. Piemēram, ļaujiet
z1 = 3 - 4j un z2 = 2 + 3j
Ar tiešo komponentu reizināšanu:
z1z2 = (3 - 4j) (2 + 3j) = 6-8j +9j + 12 = 18 + j
vai izmantojot formulu: z1z2 = a1 a2- b1b2 + j(b1a2+ b2a1)
z1z2 = 6 + 12 + j (-8 + 9) = 18 + j
Mēs domājam, ka, ja izmantojat šo formulu, visticamāk, veicat kļūdu, nekā tad, ja sastāvdaļas reizināt tieši.
z1: = 3-4 * j
z2: = 2 + 3 * j
z1 * z2 = [18 + 1 * j]
importēt matemātiku kā m
importēt cmath kā c
z1=komplekss('3-4j')
z2=komplekss('2+3j')
drukāt (“z1*z2=”,z1*z2)
Polāro vai eksponenciālo formu kompleksu skaitļu reizināšana
Lai veiktu šo darbību, reiziniet absolūtās vērtības un pievienojiet abu kompleksu skaitļu leņķus. Ļaujiet:
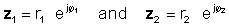
Tad izmantojiet eksponenciālo funkciju reizināšanas noteikumu:
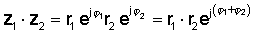
vai polārā formā
z1 z2 = r1 r2 ∠ φ1 + φ2
Piezīme. Mēs jau esam izmantojuši šo noteikumu, kad mēs aprēķinājām zz *virs. Tā kā konjugāta leņķim ir pretēja sākotnējā leņķa zīme, kompleksais skaitlis, kas reizināts ar paša konjugātu, vienmēr ir reāls skaitlis; proti, tās absolūtās vērtības kvadrāts: zz * = r2
Piemēram, ļaujiet:
z1 = 5 ∠ 30 ° un z2 = 4 ∠ -60 °
tAD
z1z2 = 20 ∠ -30 °
vai eksponenciālā veidā
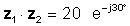
Reizināšana ir acīmredzami vienkāršāka, ja skaitļi ir polārā vai eksponenciālā formā.
Tomēr, ja sarežģītie skaitļi ir doti taisnstūra formā, jums jāapsver tieša reizināšanas veikšana, kā parādīts iepriekš, jo, ja skaitļus konvertējat pirms to reizināšanas, ir jāveic papildu darbības. Vēl viens faktors, kas jāapsver, ir tas, vai vēlaties, lai atbildes būtu taisnstūra vai polārā / eksponenciālā formā. Piemēram, ja divi skaitļi ir taisnstūra formā, bet jūs vēlaties, lai to produkts būtu polārs, ir jēga tos nekavējoties pārveidot un pēc tam reizināt.
Dalīšana
Komplekso skaitļu sadalīšanai ir divas metodes -
Sarežģītu numuru sadalījums taisnstūra formā
Lai veiktu operāciju, reiziniet skaitītāju un saucēju ar saucēja konjugātu. Saucējs kļūst par reālu skaitli, un dalījums tiek reducēts līdz divu sarežģītu skaitļu reizinājumam un dalīšanai ar reālu skaitli, saucēja absolūtās vērtības kvadrātu.
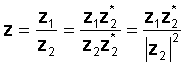
Piemēram, ļaujiet:
z1 = 3 - 4j un z2 = 2 + 3j
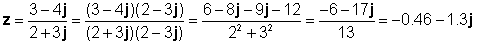
Pārbaudīsim šo rezultātu ar TINA tulku:
z1: = 3-4 * j
z2: = 2 + 3 * j
z1 / z2 = [- 461.5385m-1.3077 * j]
importēt matemātiku kā m
importēt cmath kā c
z1=komplekss('3-4j')
z2=komplekss('2+3j')
drukāt (“z1/z2=”,z1/z2)
Sarežģītu skaitļu sadalījums, kas dots polārā vai eksponenciālā veidā
Lai veiktu operāciju, sadaliet absolūtās vērtības (lielumus) un atņemiet saucēja leņķi no skaitītāja leņķa. Ļaujiet:
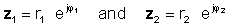
tad izmantojot eksponenciālo funkciju dalīšanas noteikumu
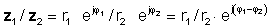
vai polārā formā
z 1 / z2 = r1 / r2 ∠ φ 1- φ 2
Piemēram, ļaujiet:
z 1 = 5 ∠ 30 ° un z 2 = 2 ∠ -60 °
tAD
z 1 / z2 = 2.5 = 90 °
vai eksponenciālās un taisnstūra formas
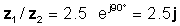
Pārbaudīsim šo rezultātu ar TINA tulku:
z1: = 5 * exp (j * degtorad (30))
z2: = 2 * exp (j * degtorad (-60))
z1 / z2 = [0 + 2.5 * j]
importēt matemātiku kā m
importēt cmath kā c
z1=5*(c.exp(komplekss(0,m.radiāni(30))))
z2=2*(c.exp(komplekss(0,m.radiāni(-60))))
drukāt (“z1/z2=”,z1/z2)
Sadalīšana acīmredzami ir vienkāršāka, ja skaitļi ir polāri vai eksponenciāli.
Tomēr, ja sarežģītie skaitļi ir norādīti taisnstūra formā, jums jāapsver dalīšanas iespēja tieši izmantojot sarežģīto konjugēto metodi, kā parādīts iepriekš, jo, ja skaitļi tiek pārveidoti pirms sadalīšanas, ir jāveic papildu darbības. Vēl viens faktors, kas jāapsver, ir tas, vai vēlaties, lai atbildes būtu taisnstūra vai polārā / eksponenciālā formā. Piemēram, ja divi skaitļi ir taisnstūra formā, bet jūs vēlaties, lai to koeficients būtu polārs, ir jēga tos nekavējoties pārveidot un pēc tam sadalīt.
Tagad ilustrēsim sarežģītus skaitļus, izmantojot vairāk skaitlisku problēmu. Kā parasti, mēs pārbaudīsim mūsu risinājumus, izmantojot TINA tulku. Tulks strādā ar radiāniem, bet tam ir standarta funkcijas radianu pārvēršanai grādos vai otrādi.
piemērs 1 Atrodiet polāro attēlojumu:
z = 12 - j 48
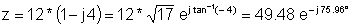
z: = 12-j * 48;
abs (z) = [49.4773]
loka (z) = [- 1.3258]
radtodeg (loka (z)) = [- 75.9638]
importēt matemātiku kā m
importēt cmath kā c
z=12-komplekss(48j)
drukāt (“abs(z)=”,abs(z))
drukāt(“loka(z)=”,c.fāze(z))
print(“grādi(loka(z))=”,m.grādi(c.fāze(z)))
piemērs 2 Atrodiet taisnstūra attēlojumu:
z = 25 e j 125 °
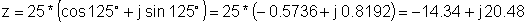
z: = 25 * exp (j * (degtorad (125)));
z = [- 14.3394 + 20.4788 * j]
Re (z) = [- 14.3394]
Im (z) = [20.4788]
importēt matemātiku kā m
importēt cmath kā c
z=25*c.exp(komplekss(0,m.radiāni(125)))
drukāt (“z=”,z)
drukāt (“real(z)=”,z.real)
drukāt (“imag(z)=”,z.imag)
piemērs 3 Atrodiet šādu komplekso numuru polāro attēlojumu:
z 1 = 12 + j 48 z2 = 12 - j48 z3= -12 + j 48 z4= -12 - j 48
Visu četru skaitļu absolūtās vērtības ir vienādas, jo absolūtā vērtība nav atkarīga no zīmēm. Tikai leņķi ir atšķirīgi.
z1: = 12 + j * 48;
abs (z1) = [49.4773]
loka (z1) = [1.3258]
radtodeg (loka (z1)) = [75.9638]
z2: = 12-j * 48;
abs (z2) = [49.4773]
loka (z2) = [- 1.3258]
radtodeg (loka (z2)) = [- 75.9638]
z3: = - 12 + j * 48;
abs (z3) = [49.4773]
loka (z3) = [1.8158]
radtodeg (loka (z3)) = [104.0362]
z4: = - 12-j * 48:
abs (z4) = [49.4773]
loka (z4) = [- 1.8158]
radtodeg (loka (z4)) = [- 104.0362]
importēt matemātiku kā m
importēt cmath kā c
z1=komplekss('12+48j')
drukāt (“abs(z1)=”,abs(z1))
drukāt(“loka(z1)=”,c.fāze(z1))
print(“grādi(loka(z1))=”,m.degrees(c.phase(z1)))
z2=komplekss('12-48j')
drukāt (“abs(z2)=”,abs(z2))
drukāt(“loka(z2)=”,c.fāze(z2))
print(“grādi(loka(z2))=”,m.degrees(c.phase(z2)))
z3=komplekss('-12+48j')
drukāt (“abs(z3)=”,abs(z3))
drukāt(“loka(z3)=”,c.fāze(z3))
print(“grādi(loka(z3))=”,m.degrees(c.phase(z3)))
z4=komplekss('-12-48j')
drukāt (“abs(z4)=”,abs(z4))
drukāt(“loka(z4)=”,c.fāze(z4))
print(“grādi(loka(z4))=”,m.degrees(c.phase(z4)))
TINA loka () funkcija nosaka jebkura kompleksa skaitļa leņķi, automātiski pareizi ievietojot to vienā no četriem kvadrantiem.
Esiet uzmanīgi, izmantojot iedegumu-1 funkcija leņķa atrašanai, jo tā ir ierobežota ar atgriešanās leņķiem tikai pirmajā un ceturtajā kvadrantā (–90 °φ<90 °).
Kopš z1 atrodas koordinātu sistēmas pirmajā kvadrantā, aprēķins ir:
α 1 = iedegums-1(48 / 12) = iedegums-1(4) = 75.96 °
Kopš z4 atrodas koordinātu sistēmas trešajā kvadrantā, iedegums-1neatgriež pareizo leņķi. Leņķa aprēķins ir:
α 4 = 180 ° + 75.96 ° = 255.96 ° vai -360 ° + 255.96 ° = - 104.04 °, kas ir tāds pats kā aprēķināts TINA.
z2 atrodas koordinātu sistēmas ceturtajā kvadrantā. Leņķa aprēķins ir:
α 2 = iedegums-1(-48 / 12) = iedegums-1(-4) = -75.96 °
z3, tomēr ir koordinātu sistēmas 2nd kvadrantā, tā iedegums-1 neatgriež pareizo leņķi. Leņķa aprēķins ir:
α 3 = 180 ° -75.96 ° = 104.04 °.
piemērs 4 Mums ir divi sarežģīti numuri: z1= 4 - j 6 un z2 = 5 ej45 ° .
atrast z3 = z1 + z2; z4 = z1 - z2; z5 = z1 * z2; z6 = z1 / z2
Vispirms mēs risinām problēmu, izmantojot TINA tulku
{TINA tulka risinājums} |
Ievērojiet, kā TINA bez grūtībām apstrādā divus dažādos veidos norādītos sarežģītos numurus.
Bez tulka risinājums ir sarežģītāks. Lai varētu salīdzināt dažādas reizināšanas un dalīšanas metodes, vispirms noteiksim polāro formu z1 un taisnstūra forma z2 .
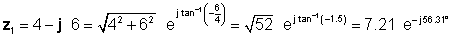
Tālāk mēs atrodam četrus risinājumus, izmantojot vispirms vienkāršākās formas: taisnstūrveida saskaitīšanai un atņemšanai un eksponenciālu reizināšanai un dalīšanai:
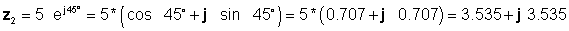
z 3 = z1 + z2 = 4 - j 6 + 3.535 + j 3.535 = 7.535 - j2.465
z 4 = z1 - z2 = 4 - j 6 - 3.535 - j 3.535 = 0.465 - j9.535
z 5 = z1 * z2 = 7.21 * 5 * ej(-56.31 ° + 45 °) = 36.05 e -j11.31 ° = 36.03 * (cos (-11.31 °) +)j* grēks (-11.31 °))
z 5 = 35.33 - j 7.07
z 6 = z1/z2= (7.21 / 5) * e j (-56.31 ° -45 °) = 1.442 e - j 101.31 ° = 1.442 (cos (-101.31 °) +)j* grēks (-101.31 °))
z 6 = -0.2828 - j 1.414
kas piekrīt TINA tulka rezultātiem.
Reizinājums, kas veikts taisnstūra formā:
z 5 =z1*z2 = (4-j6) * 3.535 * (1 +j) = 7.07 * (2-j3) * (1 +j) = 7.07 * (2-j3+j2 + 3) = 7.07 * (5-j) = 35.35-j7.07
Visbeidzot, sadalīšana veikta taisnstūra formā:
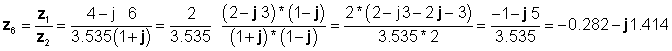
kas piekrīt iepriekšējiem rezultātiem.

