Lai izmantotu TINACloud un atlasītu interaktīvo līdzstrāvas režīmu, lai analizētu tos tiešsaistē, noklikšķiniet uz zemāk esošās piemēru shēmas vai pieskarieties tam.
Lai izmantotu TINACloud un atlasītu interaktīvo līdzstrāvas režīmu, lai analizētu tos tiešsaistē, noklikšķiniet uz zemāk esošās piemēru shēmas vai pieskarieties tam. Iegūstiet zemu izmaksu piekļuvi TINACloud, lai rediģētu piemērus vai izveidotu savas shēmas
Vēl viens veids, kā vienkāršot visu Kiršhofa vienādojumu komplektu, ir acs vai cilpas strāvas metode. Izmantojot šo metodi, Kiršhofa pašreizējie likumi tiek izpildīti automātiski, un cilpu vienādojumi, kurus mēs rakstām, atbilst arī Kiršhofa sprieguma likumiem. Kiršhofa pašreizējā likuma apmierināšana tiek panākta, katrai shēmas neatkarīgajai cilpai piešķirot slēgtas strāvas cilpas, ko sauc par acu vai cilpu strāvām, un izmantojot šīs strāvas, lai izteiktu visus pārējos ķēdes lielumus. Tā kā cilpas strāvas ir slēgtas, no mezgla jāizplūst arī strāvai, kas ieplūst mezglā; tāpēc mezglu vienādojumu rakstīšana ar šīm straumēm noved pie identitātes.
Vispirms apskatīsim acu strāvu metodi.
Vispirms mēs atzīmējam, ka acs strāvas metode ir piemērojama tikai “plakanām” shēmām. Plakanajām shēmām, šķērsojot plakni, nav šķērsojuma vadu. Bieži vien, pārzīmējot shēmu, kas šķietami nav plāna, jūs varat noteikt, ka tā faktiski ir plakana. Plānajām shēmām izmantojiet cilpas strāvas metode aprakstīts šajā nodaļā.
Lai izskaidrotu acu straumju ideju, iedomājieties ķēdes zarus kā “zvejas tīklu” un katram tīkla acim piešķiriet tīkla strāvu. (Dažreiz mēdz arī teikt, ka katrā ķēdes “logā” tiek piešķirta slēgta strāvas cilpa.)
  Shematiskā diagramma   “Zvejas tīkls” vai shēmas diagramma |
Ķēdes attēlošanas metode ar vienkāršu zīmējumu, ko sauc par a diagramma, ir diezgan spēcīgs. Kopš Kiršhofa likumi nav atkarīgi no sastāvdaļu rakstura, jūs varat neņemt vērā betona komponentus un aizstāt tos ar vienkāršiem līnijas segmentiem, Nozares grafika. Ķēžu attēlošana ar grafikiem ļauj izmantot matemātiskās metodes diagrammas teorija. Tas palīdz mums izpētīt shēmas topoloģisko raksturu un noteikt neatkarīgās cilpas. Atgriezieties vēlāk šajā vietnē, lai uzzinātu vairāk par šo tēmu.
Tīkla acu analīzes soļi:
Katrai acij piešķiriet strāvas stiprumu. Lai arī virziens ir patvaļīgs, parasti tiek izmantots virziens pulksteņrādītāja virzienā.
Ap katru acu piemēro Kiršhofa sprieguma likumu (KVL) tajā pašā virzienā kā acs strāvas. Ja rezistoram caur to ir divas vai vairāk acu strāvas, kopējo strāvu caur rezistoru aprēķina kā acu strāvu algebrisko summu. Citiem vārdiem sakot, ja strāvai, kas plūst caur rezistoru, ir tāds pats virziens kā cilpas acs strāvai, tai ir pozitīva zīme, pretējā gadījumā negatīva zīme summā. Sprieguma avotus ņem vērā kā parasti. Ja to virziens ir vienāds ar acs strāvu, to spriegumu KVL vienādojumos uzskata par pozitīvu, pretējā gadījumā negatīvu. Parasti strāvas avotiem caur avotu plūst tikai viena acs strāva, un šai strāvai ir tāds pats virziens kā avota strāvai. Ja tas tā nav, izmantojiet vispārīgāku cilpas strāvas metodi, kas aprakstīta vēlāk šajā punktā. Nav nepieciešams rakstīt KVL vienādojumus cilpām, kurās ir acu strāvas, kas piešķirtas pašreizējiem avotiem.
Atrisiniet radušos cilpas vienādojumus acu strāvām.
Izmantojot acs strāvas, nosakiet nepieciešamo strāvu vai spriegumu ķēdē.
Ļaujiet mums ilustrēt metodi ar šādu piemēru:
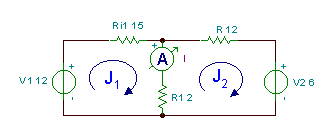
Atrodiet strāvu zemāk esošajā ķēdē.
Mēs redzam, ka šajā shēmā ir divas acis (vai kreisais un labais logs). Piešķirsim acs pulksteņrādītāja virzienā J1 un Dž2 uz acīm. Tad mēs rakstām KVL vienādojumus, pēc Ohma likuma izsakot spriegumus visā rezistoros:
-V1 + J1* (Ri1+R1) - J2*R1 = 0
V2 - J1*R1 + J2* (R + R1) = 0
Skaitliski:
-12 + J1* 17 - J2* 2 = 0
6 - Dž1* 2 + J2* 14 = 0
Izteikt J1 no pirmā vienādojuma: J1 = 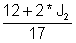

reiziniet ar 17: 102 - 24 + 4 * Dž2 + 238 * J2 = 0 līdz ar to J2 = 
un Dž1 = 
Visbeidzot, vajadzīgā strāva:
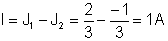
{Acu pašreizējā metode}
Sys J1, J2
J1*(Ri1+R1)-J2*R1-V1=0
J1*R1+J2*(R1+R)+V2=0
beigās;
J1 = [666.6667m]
J2 = [- 333.3333m]
I: = J1-J2;
I = [1]
importēt numpy kā n
#Izmantojiet tīkla strāvas metodi!
#Mums ir lineāra vienādojumu sistēma, kuru vēlamies atrisināt
#for I1,I2:
#I1*(Ri1+R1)+I2*Ri1-V1=0
#-V1+I1*Ri1+I2*(Ri1+R)+V2=0
#Uzrakstiet koeficientu matricu:
A=n.array([[Ri1+R1,Ri1],[Ri1,Ri1+R]])
#Uzrakstiet konstantu matricu:
b=n.masīvs([V1,V1-V2])
x=n.linalg.solve(A,b)
I1=x[0]
I2=x[1]
drukāt(“I1= %.3f”%I1)
drukāt(“I2= %.3f”%I2)
I=I1
drukāt(“I= %.3f”%I)
Pārbaudīsim rezultātus ar TINA:
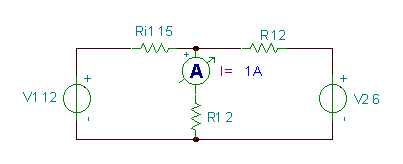

Tālāk atkal atrisināsim iepriekšējo piemēru, bet ar vispārīgāku cilpas straumju metode. Izmantojot šo metodi, tiek slēgtas slēgtās strāvas cilpas cilpas strāvas, tiek piešķirti ne vienmēr ķēdes acīm, bet gan patvaļīgiem neatkarīgas cilpas. Jūs varat pārliecināties, ka cilpas ir neatkarīgas, katrā cilpā ir vismaz viens komponents, kas nav ietverts nevienā citā cilpā. Plakanām shēmām neatkarīgo cilpu skaits ir tāds pats kā acu skaitam, ko ir viegli redzēt.
Precīzāks neatkarīgo cilpu skaita noteikšanas veids ir šāds.
Dota ķēde ar b filiāles un N mezgli. Neatkarīgo cilpu skaits l ir:
l = b - N + 1
Tas izriet no fakta, ka neatkarīgo Kirchhoff vienādojumu skaitam jābūt vienādam ar atzariem ķēdē, un mēs jau zinām, ka ir tikai N-1 neatkarīgi mezglu vienādojumi. Tāpēc kopējais Kiršhofa vienādojumu skaits ir
b = N-1 + l un līdz ar to l = b - N + 1
Šis vienādojums izriet arī no grafa teorijas pamatteormas, kas tiks aprakstīta vēlāk šajā vietā.
Tagad atkal atrisināsim iepriekšējo piemēru, bet vienkāršāk - izmantojot cilpas strāvas metodi. Izmantojot šo metodi, mēs varam brīvi izmantot cilpas acīs vai jebkuras citas cilpas, bet turēsim cilpu ar J1 ķēdes kreisajā acī. Tomēr otrajai cilpai mēs izvēlamies cilpu ar J2, kā parādīts attēlā zemāk. Šīs izvēles priekšrocība ir tā, ka J1 būs vienāda ar pieprasīto strāvu I, jo tā ir vienīgā cilpas strāva, kas iet caur R1. Tas nozīmē, ka mums nav jāaprēķina J2 vispār. Ņemiet vērā, ka atšķirībā no “īstajām” straumēm, cilpas strāvu fiziskā nozīme ir atkarīga no tā, kā mēs tās piešķiram shēmai.
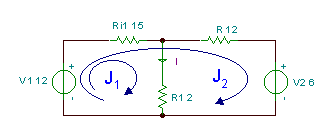

KVL vienādojumi:
J1 * (R1+Ri1) + J2 * R i1 - V1 = 0
-V1+ J1 * Ri1+ J2 * (R + R)i) + V2 = 0
un vajadzīgā strāva: I = J1
Numerically: J1*(15+2)+J2*15-12 = 0
-12 + J1 * 15 + J2 * (15 + 12) + 6 = 0
Izteikt J2 no otrā vienādojuma:
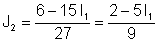
Aizstājiet pirmo vienādojumu:
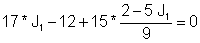
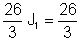
Tādējādi: J1 = I = 1 A
Citi piemēri.
piemērs 1
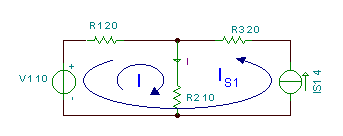
Atrodiet strāvu zemāk esošajā ķēdē.
Šajā shēmā mēs izmantojam cilpu straumju metodi. Ķēdes kreisajā logā mēs ņemam cilpas strāvu, kuru mēs apzīmējam I jo tas ir vienāds ar pieprasīto strāvu. Otra cilpas strāva ir vienāda ar Is1 avota strāvu, tāpēc mēs to apzīmējam tieši kā IS1.
Ņemiet vērā, ka šīs cilpas strāvas virziens ir nav pulksteņrādītāja virzienā, jo tā virzienu nosaka pašreizējais avots. Tā kā šī cilpas strāva jau ir zināma, nav nepieciešams rakstīt KVL vienādojumu cilpai, kur IS1 tiek pieņemts.
Tāpēc vienīgais atrisināmais vienādojums ir:
-V1 + I * R2 + R1 * (Es - esS1) = 0
līdz ar to
I = (V1 + R1 *IS1) / (R1 + R2)
Skaitliski
I=(10+20*4)/(20+10)=3 A
Varat arī ģenerēt šo rezultātu, izsaucot TINA simbolisko analīzi, no izvēlnes Analīze / Simboliskā analīze / DC Rezultāts:
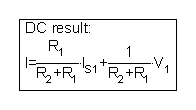
Vai arī tulks var atrisināt KVL vienādojumu:
| {TINA tulka risinājums} {Izmantot acu strāvas metodi} Sys I -V1 + I * R2 + R1 * (I - IS1) = 0 beigās; I = [3] |
Šajā piemērā ir 3 pašreizējie avoti, un to ir ļoti viegli atrisināt ar cilpas strāvas metodi.
piemērs 2
Atrast spriegumu V.
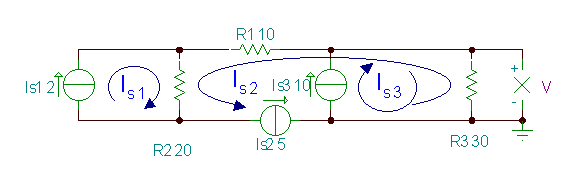

Šajā piemērā mēs varam izvēlēties trīs cilpas strāvas, lai katra caur tām šķērsotu tikai vienu strāvas avotu. Tāpēc ir zināmas visas trīs cilpas strāvas, un, izmantojot tās, mums jāizsaka tikai nezināmais spriegums V.
Padarīt strāvu algebrisko summu caur R3:
V = (IS3 - esS2) * R3= (10-5) * 30 = 150 V. To var pārbaudīt, izmantojot TINA :.
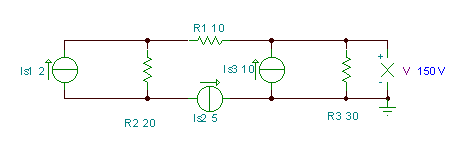

Tālāk atkal pievērsīsimies problēmai, kuru mēs jau esam atrisinājuši Kirchhoff likumi un Mezglu potenciāla metode nodaļās.
piemērs 3
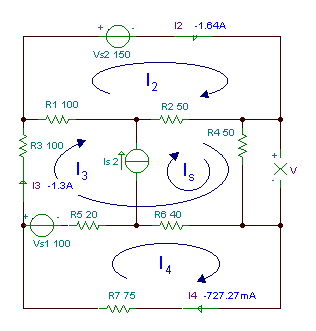
Atrodiet rezistora R spriegumu V4.
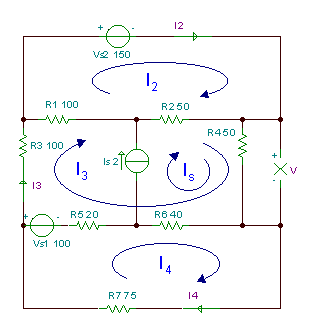

R1 = R3 = 100 omi, R2 = R4 = 50 omi, R5 = 20 omi, R6 = 40 omi, R7 = 75 omi.
Lai atrisinātu šo problēmu, iepriekšējās nodaļās bija nepieciešami vismaz 4 vienādojumi.
Atrisinot šo problēmu ar cilpas straumju metodi, mums ir četras neatkarīgas cilpas, bet, pareizi izvēloties cilpas straumes, viena no cilpas strāvām būs vienāda ar avota strāvu Is.
Balstoties uz cilpas straumēm, kas parādītas attēlā iepriekš, cilpu vienādojumi ir:
VS1+I4* (R5+R6+R7) - IS*R6 –I3* (R5 + R6) = 0
VS2 - es3* (R1+R2) - IS*R2 + I2* (R1 + R2) = 0
-VS1 + I3* (R1 + R2 + R3 + R4 + R5 + R6) + IS* (R2 +R4 + R6) - I4* (R5 + R6) - es2* (R1 + R2) = 0
Nezināms spriegums V var izteikt ar cilpas straumēm:
V = R4 * (I2 + I3)
Skaitliski:
100 + I4* 135-2 * 40-I3* 60 = 0
150 + I2* 150-2 * 50-I3* 150 = 0
–100 + I3* 360 + 2 * 140-I4* 60-I2* 150 = 0
V = 50 * (2 + I3)
Mēs varam izmantot Krāmera likumu, lai atrisinātu šo vienādojumu sistēmu:
I4 = D3/D
kur D ir sistēmas noteicošais faktors. D4, noteicējs I4, tiek veidots, aizstājot sistēmas labo pusi ar I kolonnu4koeficienti.
Vienādojumu sistēma pēc pasūtījuma:
- 60 * es3 + 135 * I4= -20
150 * I2-150 * I3 = - 50
-150 * I2+ 360 * I3 - 60 * I4= - 180
Tātad noteicošais D:
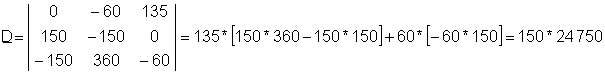
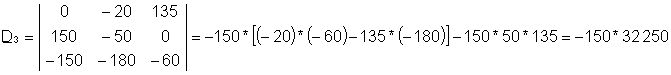
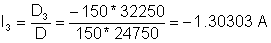
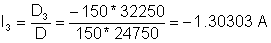
Šīs vienādojumu sistēmas risinājums ir:
V = R4* (2 + I3) = 34.8485 V
Jūs varat apstiprināt atbildi, izmantojot TINA aprēķināto rezultātu.
Sys I2, I3, I4
Vs2+I2*(R1+R2)-R2*Is-I3*(R1+R2)=0
-Vs1+I3*(R1+R2+R3+R4+R5+R6)+Is*(R2+R4+R6)-I2*(R1+R2)-I4*(R5+R6)=0
Vs1+I4*(R5+R6+R7)-Is*R6-I3*(R5+R6)=0
beigās;
I2 = [- 1.6364]
I3 = [- 1.303]
I4 = [- 727.2727m]
V: = R4 * (Is + I3);
V = [34.8485]
importēt numpy kā n
#Mums ir lineāra vienādojumu sistēma, kuru vēlamies atrisināt
#for I1,I2,I3,I4:
#I1=Ir
#Vs2+I2*(R1+R2)-R2*I1-I3*(R1+R2)=0
#-Vs1+I3*(R1+R2+R3+R4+R5+R6)+I1*(R2+R4+R6)-I2*(R1+R2)-I4*(R5+R6)=0
#Vs1+I4*(R5+R6+R7)-I1*R6-I3*(R5+R6)=0
#Uzrakstiet koeficientu matricu:
A=n.array([[1,0,0,0],[-R2,R1+R2,-(R1+R2),0],[R2+R4+R6,-(R1+R2),R1+R2+R3+R4+R5+R6,-(R5+R6)],[-R6,0,-(R5+R6),R5+R6+R7]])
#Uzrakstiet konstantu matricu:
b=n.masīvs([Is,-Vs2,Vs1,-Vs1])
x=n.linalg.solve(A,b)
I1,I2,I3,I4=x[0],x[1],x[2],x[3]
print(“I1= %.5f”%I1) #x[0]=I1
print(“I2= %.5f”%I2) #x[1]=I2
print(“I3= %.5f”%I3) #x[2]=I1
print(“I4= %.5f”%I4) #x[3]=I2
V=R4*(I1+I3)
drukāt (“V= %.5f”%V)
Šajā piemērā katra nezināmā cilpas strāva ir atzara strāva (I1, I3 un I4); tāpēc rezultātu ir viegli pārbaudīt, salīdzinot ar TINA DC analīzes rezultātiem.