Lai izmantotu TINACloud un atlasītu interaktīvo līdzstrāvas režīmu, lai analizētu tos tiešsaistē, noklikšķiniet uz zemāk esošās piemēru shēmas vai pieskarieties tam.
Lai izmantotu TINACloud un atlasītu interaktīvo līdzstrāvas režīmu, lai analizētu tos tiešsaistē, noklikšķiniet uz zemāk esošās piemēru shēmas vai pieskarieties tam. Iegūstiet zemu izmaksu piekļuvi TINACloud, lai rediģētu piemērus vai izveidotu savas shēmas
Sinusoidālo spriegumu var raksturot ar vienādojumu:
v (t) = VM sin (ωt + Φ) vai v (t) = VM cos (ωt + Φ)
| kur | v (t) | Sprieguma momentālā vērtība voltos (V). |
| VM | Sprieguma maksimālā vai maksimālā vērtība voltos (V) | |
| T | Periods: laiks, kas nepieciešams vienam ciklam sekundēs | |
| f | Biežums - periodu skaits 1 sekundē, Hz (Hertz) vai 1 / s. f = 1 / T | |
| ω | Leņķa frekvence, izteikta radiānos / s ω = 2 * π * f vai ω = 2 * π / T. | |
| Φ | Sākotnējā fāze, kas dota radiānos vai grādos. Šis daudzums nosaka sinusa vai kosīna viļņa att = 0 vērtību. | |
| Piezīme: sinusoidālā sprieguma amplitūdu dažreiz izsaka kā VEff, efektīvā vai RMS vērtība. Tas ir saistīts ar VM saskaņā ar attiecībām VM= N2VEff, vai aptuveni VEff = 0.707 VM |
Šeit ir daži piemēri, kas ilustrē iepriekš minētos terminus.
220 V maiņstrāvas sprieguma īpašības mājsaimniecības elektrotīklos Eiropā:
Efektīvā vērtība: VEff = 220 V
Maksimālā vērtība: VM= √2 * 220 V = 311 V
Frekvence: f = 50 1 / s = 50 Hz
Leņķa frekvence: ω = 2 * π * f = 314 1 / s = 314 rad / s
Periods: T = 1 / f = 20 ms
Laika funkcija: v (t) = 311 sin (314 t)
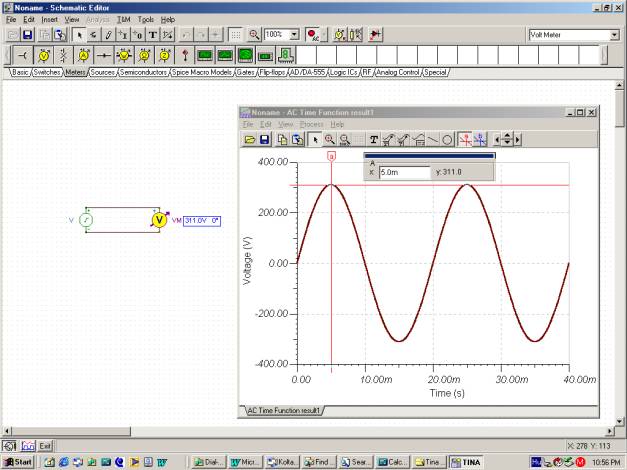
Apskatīsim laika funkciju, izmantojot komandu TINA's Analysis / AC Analysis / Time Function.
Jūs varat pārbaudīt, vai periods ir T = 20m un ka VM = 311 V.
120 V maiņstrāvas sprieguma īpašības mājsaimniecības elektrības kontaktligzdā ASV:
Efektīvā vērtība: VEff = 120 V
Maksimālā vērtība: VM= N2 120 V = 169.68 V ≈ 170 V
Frekvence: f = 60 1 / s = 60 Hz
Leņķa frekvence: ω = 2 * π * f = 376.8 rad / s ≈ 377 rad / s
Periods: T = 1 / f = 16.7 ms
Laika funkcija: v (t) = 170 sin (377 t)
Ņemiet vērā, ka šajā gadījumā laika funkciju var norādīt kā v (t) = 311 sin (314 t + Φ) vai v (t) = 311 cos (314 t + +), jo izejas sprieguma gadījumā mēs nezinu sākotnējo fāzi.
Sākotnējai fāzei ir svarīga loma, ja vienlaicīgi ir vairāki spriegumi. Labs praktisks piemērs ir trīsfāžu sistēma, kurā ir trīs spriegumi ar tādu pašu maksimālo vērtību, formu un frekvenci, un katrai no tām ir 120 ° fāzes nobīde attiecībā pret citiem. 60 Hz tīklā laika funkcijas ir:
vA(t) = 170 sin (377 t)
vB(t) = 170 grēks (377 t - 120 °)
vC(t) = 170 sin (377 t + 120 °)
Nākamajā attēlā, kas izgatavots ar TINA, redzams, ka ķēde ar šiem laikiem darbojas kā TINA sprieguma ģeneratori.
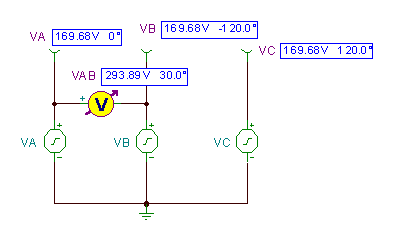

Sprieguma starpība vAB= vA(t) - vB(t) tiek parādīts kā atrisināts ar TINA analīzes / maiņas analīzes / laika funkcijas komandu.
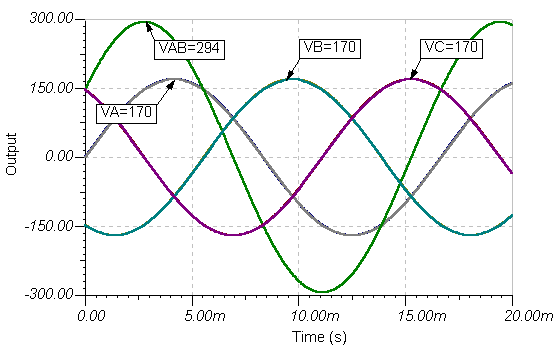

Ņemiet vērā, ka vAB (t) ir aptuveni 294 V, lielāks par 170 V virsotnēm vA(t) vai vB(t) spriegumi, bet ne tikai to maksimālo spriegumu summa. Tas ir saistīts ar fāzes atšķirībām. Mēs apspriedīsim, kā aprēķināt iegūto spriegumu (kas ir Ö3 * 170 @ 294 šajā gadījumā) vēlāk šajā nodaļā un arī atsevišķos Trīsfāžu sistēmas nodaļa.
Sinusoidālo signālu raksturīgās vērtības
Lai gan AC signāls nepārtraukti mainās laikā, ir viegli definēt dažas raksturīgās vērtības, lai salīdzinātu vienu viļņu ar citu: tās ir maksimālās, vidējās un vidējās kvadrātveida (rms) vērtības.
Mēs jau esam sasnieguši maksimālo vērtību VM , kas ir vienkārši laika funkcijas maksimālā vērtība, sinusoidālā viļņa amplitūda.
Dažreiz tiek izmantota maksimālā (pp) vērtība. Sinusoidālo spriegumu un strāvu gadījumā maksimālā vērtība ir maksimālā vērtība.
Jūsu darbs IR Klientu apkalpošana vidējā vērtība sinusa vilnis ir pozitīvā pusi cikla vērtību vidējais aritmētiskais. To sauc arī absolūtais vidējais tas ir tāds pats kā viļņa formas absolūtās vērtības vidējais lielums. Praksē mēs saskaramies ar šo vilnim rektifikācija sinusa vilnis ar ķēdi, ko sauc par pilnu viļņu taisngriezi.
Var pierādīt, ka sinusoidālā viļņa absolūtais vidējais rādītājs ir:
VAV= 2 / π VM N 0.637 VM
Ņemiet vērā, ka vidējā cikla vērtība ir nulle.
Sinusoidālā sprieguma vai strāvas vidējā vērtība vai efektīvā vērtība atbilst ekvivalentai līdzstrāvas vērtībai, kas rada tādu pašu sildīšanas jaudu. Piemēram, spriegums ar efektīvu 120 V vērtību rada tādu pašu apsildes un apgaismojuma jaudu spuldzē, kā tas ir 120 V no līdzstrāvas sprieguma avota. Var pierādīt, ka sinusoidālā viļņa vidējā vērtība vai efektīvā vērtība ir:

Vrms = VM / √2 ≅ 0.707 VM
Šīs vērtības var aprēķināt vienādi gan spriegumiem, gan strāvām.
RMS vērtība praksē ir ļoti svarīga. Ja vien nav norādīts citādi, strāvas līnijas maiņstrāvas spriegumi (piemēram, 110V vai 220V) ir norādīti vidējās vērtības vērtībās. Lielākā daļa maiņstrāvas mērītāju ir kalibrēti vidējā vērtībā un norāda vidējo robežu.
piemērs 1 Atrodiet sinusoidālā sprieguma maksimālo vērtību elektriskajā tīklā ar 220 V rms vērtību.
VM = 220 / 0.707 = 311.17 V
piemērs 2 Atrodiet sinusoidālā sprieguma maksimālo vērtību elektriskajā tīklā ar 110 V rms vērtību.
VM = 110 / 0.707 = 155.58 V
piemērs 3 Atrast sinusoidālā sprieguma (absolūtā) vidējo vērtību, ja tā vidējā vērtība ir 220 V.
Va = 0.637 * VM = 0.637 * 311.17 = 198.26 V
piemērs 4 Atrast sinusoidālā sprieguma absolūto vidējo vērtību, ja tā vidējā vērtība ir 110 V.
2 parauga sprieguma maksimums ir 155.58 V un tādējādi:
Va = 0.637 * VM = 0.637 * 155.58 = 99.13 V
piemērs 5 Atrast attiecību starp absolūto vidējo vērtību (Va) un sinusoidālās viļņu formas vidējās vērtības (V).
V / Va = 0.707 / 0.637 = 1.11
Ņemiet vērā, ka maiņstrāvas ķēdē nevar pievienot vidējās vērtības, jo tas rada nepareizus rezultātus.
FASORI
Kā jau iepriekš redzējām, maiņstrāvas ķēdēs bieži vien ir nepieciešams pievienot sinusoidālus spriegumus un vienādas frekvences strāvas. Lai gan signālus var pievienot skaitliski, izmantojot TINA, vai izmantojot trigonometriskās attiecības, ir ērtāk izmantot tā saukto fazors metode. Fasors ir komplekss skaitlis, kas attēlo sinusoidālā signāla amplitūdu un fāzi. Ir svarīgi atzīmēt, ka fazors neatspoguļo frekvenci, kam jābūt vienādam visiem fazoriem.
Fasoru var apstrādāt kā kompleksu numuru vai grafiski attēlot kā plakanu bultiņu kompleksā plaknē. Grafisko attēlojumu sauc par fazora diagrammu. Izmantojot phasor diagrammas, varat pievienot vai atņemt fazorus kompleksā plaknē ar trīsstūra vai paralelogrammas noteikumu.
Ir divi sarežģītu numuru veidi: taisnstūra un polārs.
Taisnstūra attēlojums ir formā + jb, kur j = Ö-1 ir iedomātā vienība.
Polārais attēlojums ir Ae formāj j , kur A ir absolūtā vērtība (amplitūda) un. \ t f ir fasora leņķis no pozitīvās ass, pretēji pulksteņrādītāja virzienam.
Mēs izmantosim tapa burtus sarežģītiem daudzumiem.
Tagad aplūkosim, kā iegūt atbilstošo fazoru no laika funkcijas.
Pirmkārt, pieņemsim, ka visi ķēdes spriegumi ir izteikti kosinitātes funkciju veidā. (Visi spriegumi var tikt pārvērsti šajā formā.) Tad fazors atbilst spriegumam v (t) = VM cos ( w t+f) ir: VM = VMe jf , ko sauc arī par sarežģīto maksimālo vērtību.
Piemēram, apsveriet spriegumu: v (t) = 10 cos ( w t + 30°)
Atbilstošais fazors ir: 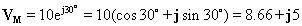
Tādā pašā veidā mēs varam aprēķināt laika funkciju no fasora. Vispirms mēs rakstām fazoru polārā formā, piem VM = VMe jr un tad atbilstošā laika funkcija ir
v (t) = VM (cos (wt+r).
Piemēram, apsveriet fasoru VM = 10 - j20 V
Liekot to polārajā formā:
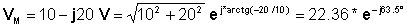
Un tāpēc laika funkcija ir: v (t) = 22.36 cos (wt - 63.5°) V
Fasori bieži tiek izmantoti, lai noteiktu spriegumu un strāvu komplekso efektīvo vai rms vērtību maiņstrāvas ķēdēs. Ņemot vērā v (t) = VMcos (wt+r) = 10cos (wt + 30°)
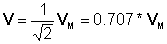
Skaitliski:
v (t) = 10 * cos (wt-30°)
Sarežģītā efektīvā (rms) vērtība: V = 0.707 * 10 * e- j30° = 7.07 e- j30° = 6.13 - j 3.535
Pretēji: ja sprieguma kompleksā efektīvā vērtība ir:
V = - 10 + j 20 = 22.36 e j 116.5°
tad sarežģītā maksimālā vērtība: 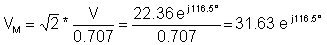
un laika funkcija: v (t) = 31.63 cos ( wt + 116.5° ) V
Īss iepriekš minēto paņēmienu pamatojums ir šāds. Ņemot vērā laika funkciju
VM (cos ( w t+r), definēsim sarežģīta laika funkcija kā:
v (t) = VM e jr e jwt = VMe jwt = VM (cos (r) + j grēks (r)) e jwt
kur VM =VM e j r t = VM (cos (r) + j grēks (r)) ir tikai iepriekš minētais fazors.
Piemēram, v (t) = 10 cos sarežģītā laika funkcija (wt + 30°)
v (t) = VMe jwt = 10 e j30 e jwt = 10e jwt (cos (30) +) j sin (30)) = e jwt (8.66 +j5)
Ieviešot sarežģītu laika funkciju, mums ir pārstāvība gan ar reālu, gan iedomātu daļu. Mēs vienmēr varam atgūt sākotnējo reālo laika funkciju, ņemot vērā mūsu rezultāta patieso daļu: v (t) = Re {v(t)}
Tomēr sarežģītajai laika funkcijai ir liela priekšrocība, ka, tā kā visām sarežģītajām laika funkcijām apskatāmajās maiņstrāvas ķēdēs ir vienāds ejwt reizinātājs, mēs varam to izdarīt un strādāt tikai ar fazoriem. Turklāt praksē mēs neizmantojam ejwt daļa vispār - tikai transformācijas no laika funkcijām uz fāzēm un atpakaļ.
Lai parādītu fasoru izmantošanas priekšrocības, aplūkosim šādu piemēru.
piemērs 6 Atrodiet spriegumu summu un starpību:
v1 = 100 cos (314 * t) un v2 = 50 cos (314 * t-45°)
Vispirms uzrakstiet abu spriegumu fāzes:
V1M = 100 V2M= 50 e - j 45° = 35.53 - j 35.35
Tādējādi:
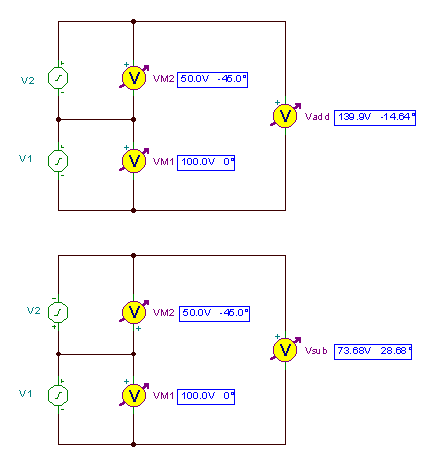
Vpievienot = V1M + V2M = 135.35 - j 35.35 = 139.89 e- j 14.63°
Vzemāk = V1M - V2M = 64.65 + j35.35 = 73.68 un j 28.67°
un pēc tam laika funkcijas:
vpievienot(t) = 139.89 * cos (wt - 14.63°)
vzemāk(t) = 73.68 * cos (wt + 28.67°)
Kā redzams šajā vienkāršajā piemērā, metode, ko izmanto phasors.is, ir ārkārtīgi spēcīgs instruments AC problēmu risināšanai.
Atrisinīsim problēmu, izmantojot TINA tulka rīkus.
{v1 + v2} aprēķināšana
v1: = 100
v2: = 50 * exp (-pi / 4 * j)
v2 = [35.3553-35.3553 * j]
v1add: = v1 + v2
v1add = [135.3553-35.3553 * j]
abs (v1add) = [139.8966]
radtodeg (loka (v1add)) = [- 14.6388]
{v1-v2} aprēķināšana
v1sub: = v1-v2
v1sub = [64.6447 + 35.3553 * j]
abs (v1sub) = [73.6813]
radtodeg (loka (v1sub)) = [28.6751]
#v1+v2 aprēķins
importēt matemātiku kā m
importēt cmath kā c
v1=100
v2=50*c.exp(komplekss(0,-c.pi/4))
drukāt (“v2=”, v2)
vadd=v1+v2
drukāt (“vadd=”,vadd)
drukāt (“abs(vadd)=”,abs(vadd))
print(“grādi(loka(vadd))=”,m.degrees(c.phase(vadd)))
#v1-v2 aprēķins
vsub=v1-v2
drukāt (“vsub=”,vsub)
drukāt (“abs(vsub)=”,abs(vsub))
print(“grādi(loka(vsub))=”,m.degrees(c.phase(vsub)))
Amplitūdas un fāzes rezultāti apstiprina roku aprēķinus.
Tagad ļauj pārbaudīt rezultātu, izmantojot TINA AC analīzi.
Pirms analīzes veikšanas pārliecinieties, ka AC pamatfunkcija ia ir iestatīts kosinuss iekš Redaktora opcijas dialoglodziņš izvēlnē Skats / opcija. Mēs izskaidrosim šī parametra lomu vietnē piemērs 8.
Ķēdes un rezultāti:
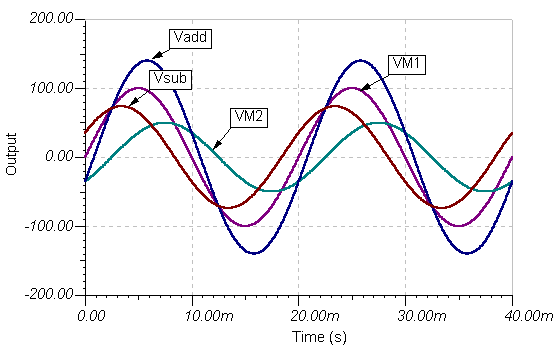
Atkal rezultāts ir vienāds. Šeit ir laika funkciju diagrammas:
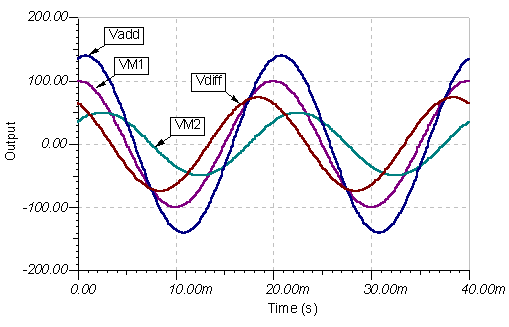
piemērs 7 Atrodiet spriegumu summu un starpību:
v1 = 100 sin (314 * t) un v2 = 50 cos (314 * t-45°)
Šis piemērs rada jaunu jautājumu. Līdz šim mēs esam pieprasījuši, lai visas laika funkcijas tiktu piešķirtas kā kosinitātes funkcijas. Ko mēs darām ar laika funkciju, kas tiek dota kā sinusa? Risinājums ir sinuso funkciju pārveidot par kosinitātes funkciju. Izmantojot trigonometrisko attiecību sin (x) = cos (x-p/ 2) = cos (x-90°), mūsu piemēru var pārformulēt šādi:
v1 = 100 cos (314t - 90°) un v2 = 50 cos (314 * t - 45°)
Tagad sprieguma fāzes ir:
V1M = 100 e - j 90° = -100 j V2M= 50 e - j 45° = 35.53 - j 35.35
Tādējādi:
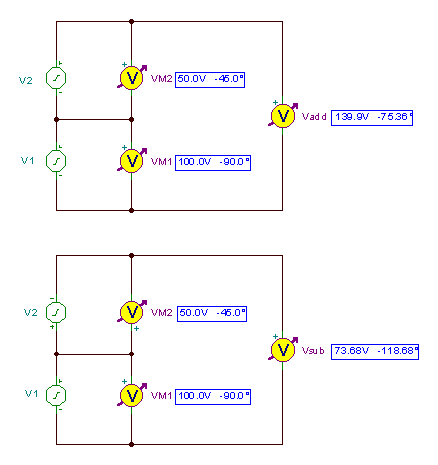
V pievienot = V1M + V2M = 35.53 - j 135.35
V zemāk = V1M - V2M = - 35.53 - j 64.47
un pēc tam laika funkcijas:
vpievienot(t) = 139.8966 cos (wt-75.36°)
vzemāk(t) = 73.68 cos (wt-118.68°)
Atrisinīsim problēmu, izmantojot TINA tulka rīkus.
{v1 + v2} aprēķināšana
v1: = - 100 * j
v2: = 50 * exp (-pi / 4 * j)
v2 = [35.3553 - 35.3553 * j]
v1add: = v1 + v2
v1add = [35.3553-135.3553 * j]
abs (v1add) = [139.8966]
radtodeg (loka (v1add)) = [- 75.3612]
{v1-v2} aprēķināšana
v1sub: = v1-v2
v1sub = [- 35.3553 - 64.6447 * j]
abs (v1sub) = [73.6813]
radtodeg (loka (v1sub)) = [- 118.6751]
#v1+v2 aprēķins
importēt matemātiku kā m
importēt cmath kā c
v1=100
v2=50*c.exp(komplekss(0,-c.pi/4))
drukāt (“v2=”, v2)
vadd=v1+v2
drukāt (“vadd=”,vadd)
drukāt (“abs(vadd)=”,abs(vadd))
print(“grādi(loka(vadd))=”,m.degrees(c.phase(vadd)))
#v1-v2 aprēķins
vsub=v1-v2
drukāt (“vsub=”,vsub)
drukāt (“abs(vsub)=”,abs(vsub))
print(“grādi(loka(vsub))=”,m.degrees(c.phase(vsub)))
Pārbaudīsim rezultātu ar TINA AC analīzi
piemērs 8
Atrodiet spriegumu summu un starpību:v1 = 100 sin (314 * t) un v2 = 50 sin (314 * t-45°)
Šis piemērs rada vēl vienu problēmu. Ko darīt, ja visi spriegumi tiek doti kā sinusviļņi, un mēs vēlamies redzēt rezultātu kā sinusa vilni ?. Mēs, protams, varētu pārvērst abus spriegumus par kosinusa funkcijām, aprēķināt atbildi un pārvērst rezultātu atpakaļ sinusa funkcijā, taču tas nav nepieciešams. Mēs varam izveidot fāzes no sinusa viļņiem tādā pašā veidā, kā mēs to darījām no kosinusa viļņiem, un pēc tam vienkārši izmantojam to amplitūdu un fāzes kā sinusa viļņu amplitūdu un fāzi.
Tas, protams, sniegs tādu pašu rezultātu kā sinuso viļņu pārveidošana par kosīna viļņiem. Kā mēs varējām redzēt iepriekšējā piemērā, tas ir vienāds ar reizināšanu ar -j un pēc tam, izmantojot cos (x) = sin (x-90°) saistība ar to pārveidošanu atpakaļ uz sinusoidālo vilni. Tas ir vienāds ar reizināšanu ar j. Citiem vārdiem sakot, kopš -j × j = 1, mēs varētu izmantot fasorus, kas iegūti tieši no sinuso viļņu amplitūdām un fāzēm, lai attēlotu funkciju un pēc tam atgrieztos pie viņiem tieši. Tāpat, saprotot tādā pašā veidā par sarežģītajām laika funkcijām, mēs varētu uzskatīt sine viļņus kā sarežģītu laika funkciju iedomātas daļas un papildināt tās ar kosinitātes funkciju, lai radītu pilnīgu komplekso laika funkciju.
Apskatīsim šī piemēra risinājumu, izmantojot sinusa funkcijas kā fāzes pamatu (pārveidojot grēku ( w t) uz reālās vienības fāzu (1)).
V1M = 100 V2M= 50 e - j 45° = 35.53 - j 35.35
Tādējādi:
V pievienot = V1M + V2M = 135.53 - j 35.35
V zemāk = V1M - V2M = 64.47+ j 35.35
Ņemiet vērā, ka fasori ir tieši tādi paši kā 6, bet ne laika funkcijas:
v3(t) = 139.9sin (wt - 14.64°)
v4(t) = 73.68sin (wt + 28.68°)
Kā redzat, rezultātu ir ļoti viegli iegūt, izmantojot sinusa funkcijas, it īpaši, ja mūsu sākotnējie dati ir sinusa viļņi. Daudzas mācību grāmatas dod priekšroku sinusoidāla viļņa izmantošanai kā fazoru pamatfunkcijai. Praksē jūs varat izmantot jebkuru no metodēm, taču nejauciet tās.
Izveidojot fasorus, ir ļoti svarīgi, lai visas laika funkcijas vispirms tiktu konvertētas vai nu sinuso, vai kosinē. Ja jūs sākāt no sinusiskajām funkcijām, tad, atgriežoties no fasoriem uz laika funkcijām, jūsu risinājumiem jābūt ar sinusiskām funkcijām. Tas pats sakāms, ja sākat ar kosinēšanas funkcijām.
Atrisinīsim to pašu problēmu, izmantojot TINA interaktīvo režīmu. Tā kā mēs vēlamies izmantot sinuso funkcijas kā pamatu fasoru izveidei, pārliecinieties, ka AC pamatfunkcija ir iestatīts uz sine iekš Redaktora opcijas dialoglodziņš no izvēlnesView / Option.
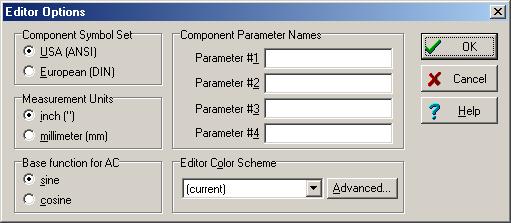

Ķēdes viļņu formu summai un atšķirībai un rezultātam:
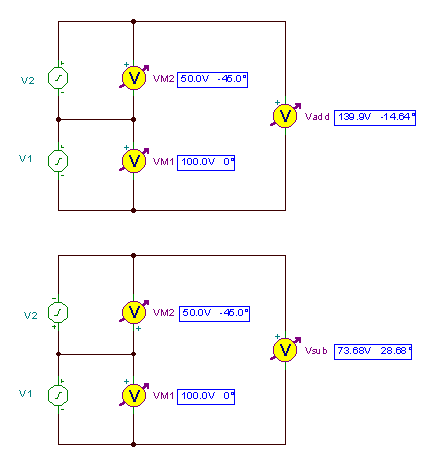
un laika funkcijas: