KIRCHHOFF likumi

Lai izmantotu TINACloud un atlasītu interaktīvo līdzstrāvas režīmu, lai analizētu tos tiešsaistē, noklikšķiniet uz zemāk esošās piemēru shēmas vai pieskarieties tam.
Iegūstiet zemu izmaksu piekļuvi TINACloud, lai rediģētu piemērus vai izveidotu savas shēmas

SUPERPOSITION THEOREM

NODE POTENCIĀLĀ METODE

Daudzas shēmas ir pārāk sarežģītas, lai tās varētu atrisināt, izmantojot virkņu vai paralēlu shēmu noteikumus vai metodes, kas paredzētas pārejai uz vienkāršākām shēmām, kas aprakstītas iepriekšējās nodaļās. Šīm shēmām mums ir vajadzīgas vispārīgākas risinājumu metodes. Vispārīgāko metodi dod Kiršofa likumi, kas ļauj aprēķināt visus ķēžu spriegumus un ķēžu strāvas, izmantojot lineāro vienādojumu sistēmas risinājumu.

Ir divi Kirhhofa likumi, sprieguma likums Un pašreizējais likumu. Šos divus likumus var izmantot, lai noteiktu visus ķēžu spriegumus un strāvas.

Kiršhofa sprieguma likums (KVL) nosaka, ka sprieguma algebriskajai summai paaugstinās un sprieguma kritumam ap cilpu jābūt nullei.

Cilpa iepriekšminētajā definīcijā nozīmē slēgtu ceļu ķēdē; tas ir, ceļš, kas atstāj mezglu vienā virzienā un atgriežas tajā pašā mezglā no cita virziena.

Mūsu piemēros cilpām izmantosim pulksteņa rādītāja virzienu; tomēr tādus pašus rezultātus iegūs, ja tiek izmantots pretēji pulksteņrādītāja virzienam.

Lai KVL piemērotu bez kļūdām, mums jādefinē tā saucamais atsauces virziens. Nezināmo spriegumu atskaites virziens norāda no pieļaujamo spriegumu līdz + - zīmei. Iedomājieties, vai izmantojat voltmetru. Jūs novietosit voltmetra pozitīvo zondi (parasti sarkanu) pie komponenta atsauces + spailes. Ja reālais spriegums ir pozitīvs, tas atrodas tajā pašā virzienā, kurā mēs pieņēmām, un gan mūsu risinājums, gan voltmetrs parādīs pozitīvu vērtību.

Atvasinot algebrisko spriegumu summu, tiem spriegumiem, kuriem atskaites virziens sakrīt ar cilpas virzienu, jāpiešķir pluszīme, bet pretējā gadījumā - negatīvas zīmes.

Vēl viens veids, kā noteikt Kiršhofa sprieguma likumu, ir: virknes ķēdes pielietotais spriegums ir vienāds ar sprieguma kritumu summu pa virknes elementiem.

Šis īsais piemērs parāda Kirhhofa sprieguma likuma izmantošanu.

Atrodiet spriegumu visā rezistorā R_2, ņemot vērā, ka avota spriegums V_S = 100 V un ka spriegums visā rezistorā R₁ir V₁ = 40 V.

Zemāk redzamo attēlu var izveidot, izmantojot TINA Pro 6. un jaunāku versiju, kurā shematiskajā redaktorā ir pieejami zīmēšanas rīki.

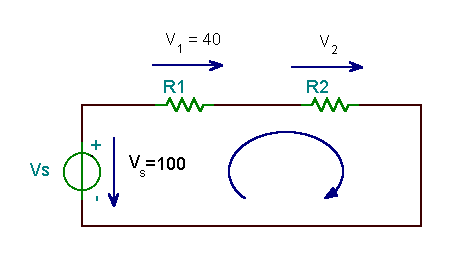
Risinājums, izmantojot Kiršhofa sprieguma likumu: -V_S + V₁ + V₂= 0 vai V_S = V₁ + V₂

līdz ar to: V₂ = V_S - V₁ = 100-40 = 60V

Ņemiet vērā, ka parasti mēs nezinām rezistoru spriegumus (ja vien mēs tos neizmērām), un risinājumam mums jāizmanto abi Kiršhofa likumi.

Kiršhofa pašreizējie likumi (KCL) nosaka, ka visu to strāvu algebriskā summa, kas ienāk un iziet no jebkura ķēdes mezgla, ir nulle.

Turpmāk mēs piešķiram + zīmi strāvām, kas atstāj mezglu, un - zīmi strāvām, kas ienāk mezglā.

Šeit ir pamata piemērs, kas parāda Kiršhofa pašreizējos likumus.

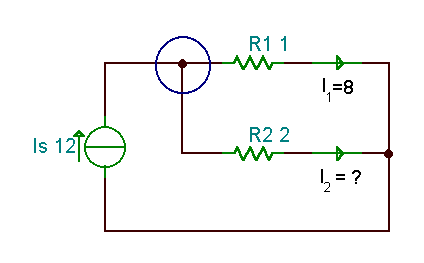
Atrodiet pašreizējo I₂ ja avota strāva I_S = 12 A, un es₁ = 8 A.

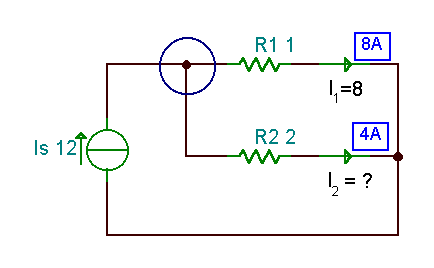
Izmantojot Kirchhoff pašreizējo likumu pie apļa mezgla: -I_S + I₁ + I₂ = 0, tātad: I₂= I_S - es₁ = 12 - 8 = 4 A, kā jūs varat pārbaudīt, izmantojot TINA (nākamais attēls).

Nākamajā piemērā mēs izmantosim gan Kiršhofa likumus, gan Ohma likumu, lai aprēķinātu strāvu un spriegumu pāri rezistoriem.

Zemāk redzamajā attēlā jūs atzīmēsit Sprieguma bultiņa virs rezistoriem. Šī ir jauna sastāvdaļa, kas pieejama TINA 6. versija un darbojas kā voltmetrs. Ja to savienojat pāri komponentam, bultiņa nosaka atskaites virzienu (lai salīdzinātu ar voltmetru, iedomājieties sarkano zondi novietot bultiņas galā un melno zondi galā). Veicot DC analīzi, uz bultiņas tiks parādīts faktiskais komponenta spriegums.

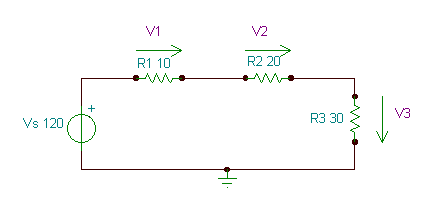
Noklikšķiniet / pieskarieties iepriekš minētajai ķēdei, lai analizētu on-line, vai noklikšķiniet uz šīs saites, lai saglabātu sistēmā Windows

Lai sāktu izmantot Kiršhofa pašreizējos likumus, mēs redzam, ka strāvas caur visām sastāvdaļām ir vienādas, tāpēc apzīmēsim šo strāvu ar I.

Saskaņā ar Kiršhofa sprieguma likumu: V_S = V₁+V₂+V₃

Tagad tiek izmantots Ohmas likums: V_S= I * R₁+ I * R₂+ I * R₃

Un no šejienes ķēdes strāva:

I = V_S/ (R₁+R₂+R₃) = 120 / (10 + 20 + 30) = 2 A

Visbeidzot, rezistoru spriegumi:

V₁= I * R₁ = 2 * 10 = 20 V; V₂ = I * R₂ = 2 * 20 = 40 V; V₃ = I * R₃ = 2 * 30 = 60 V

Tādi paši rezultāti būs redzami sprieguma bultiņās, vienkārši palaižot TINA interaktīvo līdzstrāvas analīzi.

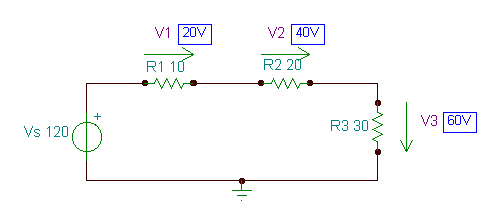
Šajā nākamajā, sarežģītākajā shēmā mēs arī izmantojam gan Kiršofa likumus, gan Ohma likumus, taču mēs secinām, ka visvairāk mēs risinām lineāru vienādojumu sistēmu.

Kopējais Kiršhofa likumu neatkarīgo pielietojumu skaits ķēdē ir ķēdes atzaru skaits, savukārt nezināmo kopskaits (katras atzares strāva un spriegums) ir divreiz lielāks. Tomēr, izmantojot arī Ohma likumu pie katra rezistora un vienkāršos vienādojumus, kas definē pielietotos spriegumus un strāvas, iegūstam vienādojumu sistēmu, kurā nezināmo skaits ir vienāds ar vienādojumu skaitu.

Atrodiet zaru strāvas I1, I2, I3 zemāk esošajā ķēdē.

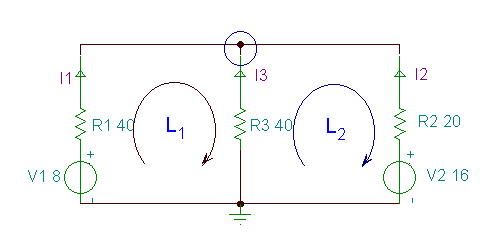
Noklikšķiniet / pieskarieties iepriekš minētajai ķēdei, lai analizētu on-line, vai noklikšķiniet uz šīs saites, lai saglabātu sistēmā Windows

Vienādojumu kopa ir šāda:

Apgrieztā mezgla mezgla vienādojums:

- I₁- I₂- es₃ = 0

vai reizinot ar -1

I₁+ I₂+ I₃ = 0

Cilpas vienādojumi (izmantojot pulksteņa rādītāja virzienā) cilpai L1, kas satur V₁, R₁ un R₃

-V₁+I₁*R₁-I₃*R₃ = 0

un cilpai L2, kas satur V₂, R₂ un R₃

I₃*R₃ - es₂*R₂ +V₂ = 0

Komponentu vērtību aizstāšana:

I₁+ I₂+ I₃ = 0 -8 + 40 * I₁ - 40 * I₃ = 0 40 * I₃ –20 * I₂ + 16 = 0

Izteikt I₁ izmantojot mezgla vienādojumu: I₁ = -I₂ - es₃

pēc tam to aizstāt ar otro vienādojumu:

-V₁- (es₂ + I₃) * R₁ –I₃*R₃ = 0 or –8- (I₂ + I₃) * 40 - I₃* 40 = 0

Izteikt I₂ un aizstāt to ar trešo vienādojumu, no kura jūs jau varat aprēķināt I₃:

I₂ = - (V₁ + I₃* (R₁+R₃)) / R₁ or I₂ = - (8 + I₃* 80) / 40

I₃*R₃ + R₂* (V₁ + I₃* (R₁+R₃)) / R₁ +V₂ = 0 or I₃* 40 + 20 * (8 + I₃* 80) / 40 + 16 = 0

Un: I₃ = - (V₂ + V₁*R₂/R₁) / (R₃+ (R₁+R₃) * R₂/R₁) or I₃ = -(16+8*20/40)/(40 + 80*20/40)

Tāpēc I₃ = - 0.25 A; I₂ = - (8-0.25 * 80) / 40 = 0.3 A un I₁ = - (0.3-0.25) = - 0.05 A

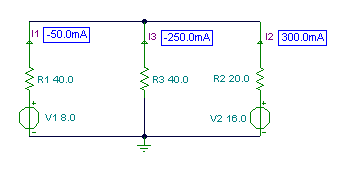
Vai: I₁ = -50 mA; I₂ = 300 mA; I₃ = -250 mA.

Tagad atrisināsim tos pašus vienādojumus ar TINA tulku:

{TINA tulka risinājums}
Sys I1, I2, I3
I1 + I2 + I3 = 0
-V1+I1*R1-I3*R3=0
I3*R3-I2*R2+V2=0
beigās;
I1 = [- 50m]
I2 = [300m]
I3 = [- 250m]

#Python risinājums
importēt numpy kā np,sympy kā s
#Mums ir lineāra sistēma
#vienādojumi, kurus vēlamies atrisināt:
#I1+I2+I3=0
#-V1+I1*R1-I3*R3=0
#I3*R3-I2*R2+V2=0

I1,I2,I3=s.symbols([‘I1′,’I2′,’I3’])
sol = s.solve([
I1+I2+I3,
-V1+I1*R1-I3*R3,
I3*R3-I2*R2+V2], [I1, I2, I3])
drukāt (sol)

A= np.array([[1,1,1],[R1,0,-R3],[0,-R2,R3]])

b= np.masīvs([0,V1,-V2])

x=np.linalg.solve(A,b)
#I1=x[0]
#I2=x[1]
#I3=x[2]
#I1
drukāt (“I1= %.3f”%x[0])
#I2
drukāt (“I2= %.3f”%x[1])
#I3
drukāt (“I3= %.3f”%x[2])

Beidzot pārbaudīsim rezultāti, izmantojot TINA:

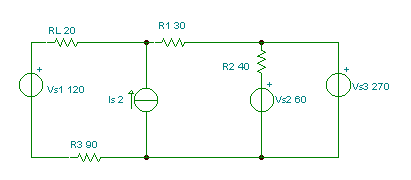
Tālāk analizēsim sekojošo vēl sarežģītāko shēmu un noteiksim tās atzarojuma strāvas un spriegumus.

Noklikšķiniet / pieskarieties iepriekš minētajai ķēdei, lai analizētu on-line, vai noklikšķiniet uz šīs saites, lai saglabātu sistēmā Windows

Apzīmēsim nezināmos spriegumus un strāvas, pievienojot komponentiem sprieguma un strāvas bultiņas, kā arī parādīsim cilpas (L1, L2, L3) un mezglus (N1, N2), kur izmantosim Kiršhofa vienādojumus.

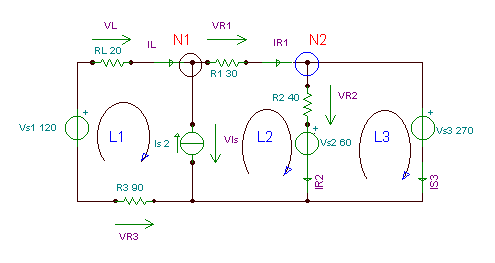Noklikšķiniet / pieskarieties iepriekš minētajai ķēdei, lai analizētu on-line, vai noklikšķiniet uz šīs saites, lai saglabātu sistēmā Windows

Šeit ir Kirhhofa vienādojumi cilpām (izmantojot pulksteņa rādītāja virzienā) un mezgliem.

-I_L+ I_R1- es_s= 0(N1)

- es_R1+ I_R2+ I_s3 = 0 (N2)

-V_s1- V_R3+ V_Is+ V_L = 0 (L1)

-V_Is+ V_s2 +V_R2+V_R1 = 0 (L2)

-V_R2- V_s2+ V_s3 = 0 (L3)

Piemērojot Ohmas likumu:

V_L= I_L*R_L

V_R1=I_R1*R₁

V_R2 = I_R2*R₂

V_R3 = - Es_L*R₃

Tas ir 9 nezināmi un 9 vienādojumi. Vienkāršākais veids, kā to atrisināt, ir izmantot TINA

tulks. Tomēr, ja mēs esam spiesti izmantot rokas aprēķinus, mēs atzīmējam, ka šo vienādojumu kopumu var viegli reducēt uz 5 nezināmu sistēmu, aizstājot pēdējos 4 vienādojumus ar L1, L2, L3 cilpu vienādojumiem. Turklāt, pievienojot vienādojumus (L1) un (L2), mēs varam novērst V_Is, samazinot problēmu uz 4 vienādojumu sistēmu 4 nezināmiem (I_L,I_R1 I_R2I_s3). Kad esam atraduši šīs straumes, mēs varam viegli noteikt V_L, V_R1, V_R2 un V_R3 izmantojot pēdējos četrus vienādojumus (Oma likumu).

Aizstājot V_L,V_R1V_R2 ,V_R3 :

-I_L+ I_R1- es_s= 0(N1)

- es_R1+ I_R2+ I_s3 = 0 (N2)

-V_s1+ I_L*R₃+ V_Is+ I_L*R_L = 0 (L1)

-V_Is+ V_s2 + I_R2*R₂+ I_R1*R₁ = 0 (Attiecībā L2)

- es_R2*R₂- V_s2+ V_s3 = 0 (L3)

Mēs pievienojam (L1) un (L2)

-I_L+ I_R1- es_s= 0(N1)

- es_R1+ I_R2+ I_s3 = 0 (N2)

-V_s1+ I_L*R₃+ I_L*R_L + V_s2 + I_R2*R₂+ I_R1*R₁ = 0 (L1) + (L2)

- es_R2*R₂- V_s2+ V_s3 = 0 (L3)

Pēc komponentu vērtību aizstāšanas viegli rodas šo vienādojumu risinājums.

-I_L+I_R1- 2 = 0 (N1)

-I_R1 + I_R2 + I_S3 = 0 (N2)

-120 - + I_L* 90 + I_L* 20 + 60 + I_R2* 40 + I_R1* 30 = 0 (L₁) + (L.₂)

-I_R2* 40 - 60 + 270 = 0 (L₃)

no L₃ I_R2 = 210 / 40 = 5.25 A (I)

no N₂ I_S3 - es_R1 = - 5.25 (II)

no L₁+L₂ 110 I_L + 30 I_R1 = -150 (III)

un N₁ I_R1 - es_L = 2 (IV)

Reiziniet (IV) ar –30 un pievienojiet (III) 140 I_L = -210 līdz ar to I_L = - 1.5 A

Aizstājējs I_L (IV) I_R1 = 2 + (-1.5) = 0.5 A

un es_R1 uz (II) I_S3 = -5.25 + I_R1 = -4,75 A

Un spriegumi: V_R1 = I_R1*R₁ = 15 V; V_R2 = I_R2*R₂ = 210 V;

V_R3 = - Es_L*R₃= 135 V; V_L = I_L*R_L = - 30 V; V_Is = V_S1+V_R3-V_L = 285 V

{TINA tulka sākotnējo vienādojumu risinājums}
Sys IL,IR1,IR2,Is3,VIs,VL,VR1,VR3,VR2
-IL-Is + IR1 = 0
-IR1 + IR2 + Is3 = 0
-Vs1 + VR3 + Vis-VL = 0
-Vis + VR1 + VR2 + Vs2 = 0
-Vs3 + VR2 + Vs2 = 0
VR1 = IR1 * R1
VR2 = IR2 * R2
VR3 = -IL * R3
VL = IL * RL
beigās;
IL = [- 1.5]
IR1 = [500m]
IR2 = [5.25]
Is3 = [- 4.75]
VIs = [285]
VL = [- 30]
VR1 = [15]
VR2 = [210]
VR3 = [135]

#Python risinājums
#Ax=b
importēt numpy kā np,sympy kā s
#Simbolisks risinājums, izmantojot numpy.solve
#Vienādojumi:
#IL=-Is+IR1
#IR1=IR2+Is3
#Vs1+VR3-Vis-VL=0
#Vis=VR1+VR2+Vs2
#Vs3=VR2+Vs2
#VR1=IR1*R1
#VR2=IR2*R2
#VR3=-IL*R3
#VL=IL*RL
#Atrisiniet:
#IL,IR1,IR2,
#Is3,Vis,VL,
#VR1,VR3,VR2

IL,IR1,IR2,Is3,Vis,VL,VR1,VR3,VR2=s.symbols([‘IL’,’IR1′,’IR2′,’Is3′,’Vis’,’VL’,’VR1′,’VR3′,’VR2′])
sol = s.solve([
-Is+IR1-IL,
IR2+Is3-IR1,
Vs1+VR3-Vis-VL,
VR1+VR2+Vs2-Vis,
VR2+Vs2-Vs3,
IR1*R1-VR1,IR2*R2-VR2,
-IL*R3-VR3,IL*RL-VL],[IL,IR1,IR2,Is3,Vis,VL,VR1,VR3,VR2])
drukāt (sol)

#Cita metode, kā atrisināt, izmantojot numpy.linalg
A=np.array(
[[-1,1,0,0,0,0,0,0,0],
[0,-1,1,1,0,0,0,0,0],
[0,0,0,0,-1,-1,0,1,0],
[0,0,0,0,-1,0,1,0,1],
[0,0,0,0,0,0,0,0,1],
[0,R1,0,0,0,0,-1,0,0],
[0,0,R2,0,0,0,0,0,-1],
[-R3,0,0,0,0,0,0,-1,0],
[RL,0,0,0,0,-1,0,0,0]])

b=np.array([Is,0,-Vs1,-Vs2,Vs3-Vs2,0,0,0,0])

x=np.linalg.solve(A,b)

#IL=x[0] IR1=x[1] IR2=x[2]
#Is3=x[3] Vis=x[4] VL=x[5]
#VR1=x[6] VR2=x[8] VR3=x[7]
drukāt (“IL= %.3f”%x[0])
drukāt (“IR1= %.3f”%x[1])
drukāt (“IR2= %.3f”%x[2])
drukāt (“Is3= %.3f”%x[3])
drukāt (“Vis= %.3f”%x[4])
drukāt (“VL= %.3f”%x[5])
drukāt (“VR1= %.3f”%x[6])
drukāt (“VR2= %.3f”%x[8])
drukāt (“VR3= %.3f”%x[7])

Samazināta vienādojumu komplekta risinājums, izmantojot tulku:

{TINA tulka samazinātā vienādojumu kopuma risinājums}
Sys Il, Ir1, Ir2, Is3
-Il + Ir1-2 = 0
-Ir1 + Ir2 + Is3 = 0
-120+110*Il+60+40*Ir2+30*Ir1=0
-40 * Ir2 + 210 = 0
beigās;
Il = [- 1.5]
Ir1 = [500m]
Ir2 = [5.25]
Is3 = [- 4.75]

Varam arī ievadīt spriegumu izteiksmes un TINA tulkam tos aprēķināt:

Il: = - 1.5;
Ir1: = 0.5;
Ir2: = 5.25;
Is3: = - 4.75;
Vl: = Il * RL;
VR1: = Ir1 * R1
Vr2: = Ir2 * R2;
Vr3: = - Il * R3;
VIs: = Vs1-Vl + Vr3;
Vl = [- 30]
Vr1 = [15]
Vr2 = [210]
Vr3 = [135]
VIs = [285]

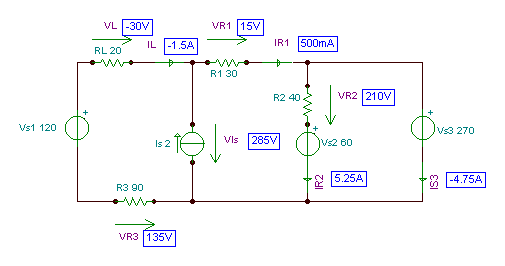Mēs varam pārbaudīt rezultātu ar TINA, vienkārši ieslēdzot TINA līdzstrāvas interaktīvo režīmu vai izmantojot analīzi / līdzstrāvas analīzi / mezglu spriegumus.

SUPERPOSITION THEOREM

NODE POTENCIĀLĀ METODE