 I-click o I-tap ang Circuits ng Halimbawa sa ibaba upang tumawag sa TINACloud at piliin ang Interactive DC mode upang Suriin ang mga ito Online.
I-click o I-tap ang Circuits ng Halimbawa sa ibaba upang tumawag sa TINACloud at piliin ang Interactive DC mode upang Suriin ang mga ito Online. Kumuha ng isang mababang gastos sa access sa TINACloud upang i-edit ang mga halimbawa o lumikha ng iyong sariling mga circuits
Sa ito at sa mga sumusunod na kabanata, ipakikita namin ang isang napakahalagang paksa: AC, o Alternating Current. Ang pangalan ng alternating kasalukuyang ay hindi masyadong tumpak at karaniwang sumasakop sa mga circuits na may mga sinusoidal voltages at alon; gayunpaman, alternating kasalukuyang ay maaari ring mangahulugan ng anumang arbitrary kasalukuyang waveform. Ang kahalagahan ng boltahe ng AC ay ang ganitong uri ng boltahe ay ginagamit para sa pangunahing pinagkukunan ng kuryente sa mga tahanan at industriya sa buong mundo. Ito rin ang batayan para sa maraming mga elektronika, telekumunikasyon, at pang-industriya na mga aplikasyon.
Upang mahawakan ang sinusoidal waveforms at ang mga circuits na nauugnay sa kanila, gagamitin namin ang simple at eleganteng paraan na tinatawag na paraan ng phasors. Ang mga Phase ay batay sa mga katangian ng mga kumplikadong numero, na perpekto para sa kumakatawan sa mga dami ng sinusoidal. Sa kabanatang ito, ibubuod namin ang mga pangunahing katotohanan tungkol sa mga kumplikadong numero at sa kanilang mga operasyon. Ipapakita rin namin kung paano ginagawang madali ng Interpreter ng TINA ang mga kalkulasyon na may mga kumplikadong numero.
Ang mga komplikadong numero ay binubuo ng dalawang bahagi, a tunay na bahagi (x), na kung saan ay isang tunay na numero, at isang tinatawag na gayon haka-haka bahagi (y), na isang tunay na bilang na pinarami ng 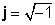
z = x + jy
saan 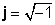
Mga halimbawa ng mga kumplikadong numero:
z 1 = 1 + j
z 2 = 4-2 j
z 3 = 3- 5j
Ang mga kumplikadong numero ay orihinal na ipinakilala sa ikalabing siyam na siglo upang kumatawan sa mga ugat ng mga polynomial na hindi maaaring kinakatawan ng mga totoong numero lamang. Halimbawa, ang mga ugat ng equation x2 + 2x + 2 = 0 ay maaari lamang inilarawan bilang 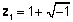
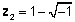
Geometriko na representasyon ng mga kumplikadong numero
Hugis pormularyo
Dahil ang isang kumplikadong numero ay palaging maaaring ihiwalay sa kanyang tunay at kumplikadong mga bahagi, maaari naming kumatawan sa isang kumplikadong numero bilang isang punto sa isang dalawang-dimensional na eroplano. Ang tunay na bahagi ng isang kumplikadong numero ay ang pagpapalabas ng punto sa totoong axis, at ang haka-haka na bahagi ng bilang ay ang paglalagay sa haka-haka na axis. Kung ang isang kumplikadong numero ay kinakatawan bilang kabuuan ng tunay at haka-haka na mga bahagi, sinasabi namin na ito ay nasa hugis-parihaba or algebraic form.
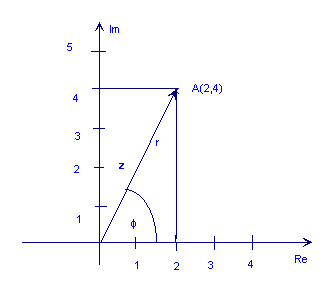
Ang sumusunod na pigura ay nagpapakita ng kumplikadong numero z = 2 + 4j
Polar at exponential form
Tulad ng nakikita mo mula sa figure sa itaas, ang punto A ay maaari ding kinakatawan ng haba ng arrow, r (tinawag din ang ganap na halaga, magnitude, o amplitude), at anggulo nito (o yugto), φ kamag-anak sa isang hindi mabuting direksyon sa direksyon sa positibong pahalang na axis. Ito ang polar anyo ng isang kumplikadong numero. Ito ay tinukoy bilang r ∠ φ.
Ang susunod na hakbang ay napakahalaga. Ang isang kumplikadong numero sa polar form ay maaari ring nakasulat sa pagpaparami anyo:
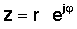
Ang simpleng ekspresyong ito ay natatangi dahil mayroon itong imahinasyong numero sa exponent sa halip na ang karaniwang tunay na numero. Ang kumplikadong eksponensyong ito ay kumikilos na ibang-iba mula sa exponential function na may isang tunay na argumento. Samantalang ex mabilis na lumalaki sa laki para sa pagtaas ng x> 0 at bumababa para sa x <0, ang pagpapaandar 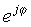
Ang pormula ni Euler ay nagbibigay ng isang unifying link sa pagitan ng mga hugis-parihaba, polar, at exponential na mga uri ng mga kumplikadong numero:
z = x + jy = re jφ = r (cos φ + j kasalanan φ )
saan 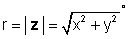
at φ = tan-1 (y / x).
Para sa aming halimbawa sa itaas, z = 2 + 4j:
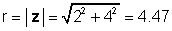
φ = tan-1 (4 / 2) = 63.4 °
samakatuwid 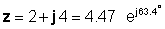
O kabaligtaran:
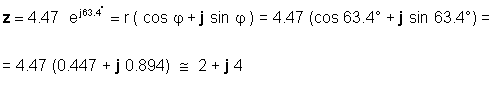
Kailangan mong maging sanay sa paggamit ng parehong mga form, depende sa application. Halimbawa, ang karagdagan o pagbabawas ay malinaw na mas madaling gawin kapag ang mga numero ay nasa hugis-parihaba na form, habang ang pagdami at paghahati ay mas madaling gawin kapag ang mga numero ay nasa exponential form.
Mga operasyon na may mga kumplikadong numero
Ang mga operasyon na maaaring gawin sa mga kumplikadong numero ay katulad sa mga para sa mga tunay na numero. Ang mga patakaran at ilang mga bagong kahulugan ay naitala sa ibaba.
Mga operasyon na may j
Ang mga operasyon sa j sundin lamang mula sa kahulugan ng haka-haka na yunit,


Upang makapagtrabaho nang mabilis at tumpak, dapat mong kabisaduhin ang mga panuntunang ito:
j 2 = -1
j 3 =-j
j 4 =1
1/j = -j
j2 = -1 ay sumusunod lamang mula sa kahulugan ng 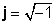
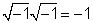
Para sa 1 /j, kami ay dumami 1 /jby j / j = 1 at makakuha j/ (jj) = j / (- 1) = -j.
Complex conjugate
Ang kumplikadong conjugate ng isang kumplikadong numero ay madaling makuha at ito ay lubos na mahalaga. Upang makuha ang kumplikadong kondyugeyt ng isang kumplikadong numero sa pormang hugis-parihaba, palitan lamang ang pag-sign ng haka-haka na bahagi. Upang gawin ito para sa isang numero sa exponential form, baguhin ang pag-sign ng anggulo ng kumplikadong numero habang pinapanatili ang ganap na halaga ng parehong.
Ang kumplikadong kondyugeyt ng isang kumplikadong numero z ay kadalasang ipinakikita ng z*.
Dahil sa kumplikadong numero z= a + jb, ang kumplikadong banghay ay z*= isang- jb.
If z ay ibinibigay sa exponential form, 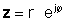
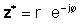
Gamit ang mga kahulugan sa itaas, madaling makita na ang isang kumplikadong numero na pinarami ng komplikadong conjugate nito ay nagbibigay ng parisukat ng lubos na halaga ng kumplikadong numero:
zz* = r2 = a2 + b2
Gayundin, sa pamamagitan ng pagdagdag o pagbabawas ng anumang kumplikadong numero at conjugate nito, nakukuha natin ang mga sumusunod na relasyon:
z + z * = 2a
samakatuwid
Re (z) = a = ( z + z * ) / 2
Katulad nito:
z - z * =j2b
samakatuwid
Im (z) = b = ( z -z * ) / 2j
Katunayan:
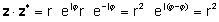
o pagpaparami ng mga tunay at haka-haka na mga bahagi at paggamit j2= -1
zz* = (a + jb) (a - jb) = a2+a jb - a jb - jbjb = a2j2 = a2 + b2
z + z* = a + jb + a - jb = 2a
z - z*= a + jb - a + jb =j2b
Mga halimbawa ng numerikal:
Sa hugis-parihaba na anyo:
z = 3 + j4
z* = 3- j4
zz * = 9 + 16 = 25
Sa polar form
z = 5 ∠ 53.13 °
z * = 5 ∠- 53.13 °
Sa exponential form:
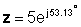
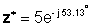
Pagdagdag at pagbawas
Ang pagdaragdag at pagbabawas ng mga kumplikadong numero ay diretso - kailangan lamang nating idagdag ang tunay at haka-haka na mga bahagi nang hiwalay. Halimbawa, kung
z1 = 3 - 4j at z2 = 2 + 3j
pagkatapos
z1 + z2 = 3 - 4j + 2 + 3j = 3 + 2 - 4j + 3j = 5 - j
z1 - z2 = 3 - 4j - 2 - 3j = 3 - 2 - 4j - 3j = 1 - j7
Malinaw, dapat nating gamitin ang hugis-parihaba na form para sa mga operasyong ito. Kung ang mga numero ay ibinibigay sa exponential o polar form, dapat natin munang ibahin ang mga ito sa hugis-parihaba na form gamit ang formula ng Euler, tulad ng ibinigay nang mas maaga.
Pagpaparami
Mayroong dalawang pamamaraan para sa pagpaparami ng mga kumplikadong numero–
Pagpaparami ng mga kumplikadong numero na ibinigay sa pormang hugis-parihaba
Upang maisagawa ang operasyon, i-multiplikate lamang ang tunay at haka-haka na mga bahagi ng isang numero na tungo sa tunay at haka-haka na bahagi ng iba pang numero at gamitin ang pagkakakilanlan j2 = -1.
z1z2 = (a1 + jb1) (a2 + jb2) = a1 a2 + jb1a2+ jb2a1 - b1b2 = a1 a2- b1b2 + j(b1a2+ jb2a1)
Kapag ang mga komplikadong numero ay binibigyan ng ayon sa bilang, hindi kinakailangan na gamitin ang formula sa itaas. Halimbawa, hayaan
z1 = 3 - 4j at z2 = 2 + 3j
Sa tuwirang pagpaparami ng mga bahagi:
z1z2 = (3 - 4j) (2 + 3j) = 6- 8j +9j + 12 = 18 + j
o gamit ang formula: z1z2 = a1 a2- b1b2 + j(b1a2+ B2a1)
z1z2 = 6 + 12 + j (-8 + 9) = 18 + j
Sa tingin namin ay mas malamang na gumawa ka ng error kung gagamitin mo ang formula kaysa sa kung direktang dumami ang mga sangkap.
z1: = 3-4 * j
z2: = 2 + 3 * j
z1 * z2 = [18 + 1 * j]
import math bilang m
import cmath bilang c
z1=kumplikado('3-4j')
z2=kumplikado('2+3j')
print("z1*z2="",z1*z2)
Pagpaparami ng mga kumplikadong numero na ibinigay sa polar o exponential form
Upang maisakatuparan ang operasyong ito, i-multiply ang mga ganap na halaga at idagdag ang mga anggulo ng dalawang komplikadong numero. Hayaan:
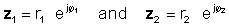
Pagkatapos ay ginagamit ang patakaran ng pagpaparami ng mga pagpaparami ng mga function:
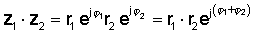
o sa polar form
z1 z2 = r1 r2 Φ1 + φ2
Tandaan: Ginamit na namin ang patakarang ito kapag kinakalkula namin zz *sa itaas. Yamang ang anggulo ng conjugate ay may kabaligtaran na pag-sign ng orihinal na anggulo, isang kumplikadong numero na pinarami ng sariling conjugate ay palaging isang tunay na numero; ibig sabihin, ang parisukat ng ganap na halaga nito: zz * = r2
Halimbawa, hayaan ang:
z1 = 5 ∠ 30 ° at z2 = 4 ∠ -60 °
pagkatapos
z1z2 = 20 ∠ -30 °
o sa exponential form
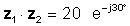
Ang pagpaparami ay malinaw na mas simple kapag ang mga numero ay nasa polar o exponential form.
Gayunpaman, kung ang mga kumplikadong numero ay ibinigay sa hugis-parihaba na form, dapat mong isaalang-alang ang pagsasagawa ng pagdaragdag nang direkta tulad ng ipinakita sa itaas, dahil may mga karagdagang hakbang kung i-convert mo ang mga numero sa polar form bago maparami ang mga ito. Isa pang kadahilanan na dapat isaalang-alang ay kung nais mo ang mga sagot na nasa hugis-parihaba form o sa polar / exponential form. Halimbawa, kung ang dalawang numero ay nasa hugis-parihaba na form ngunit nais mo ang kanilang produkto sa polar form, makatuwiran na mai-convert kaagad ang mga ito at pagkatapos ay palakihin ang mga ito.
Division
Mayroong dalawang pamamaraan para sa paghahati ng mga kumplikadong bilang–
Dibisyon ng mga kumplikadong numero na binigay sa pormang hugis-parihaba
Upang maisagawa ang operasyon, dumami ang numumerator at ang denominator sa pamamagitan ng conjugate ng denominator. Ang denominator ay nagiging isang tunay na numero at ang dibisyon ay nabawasan sa pagpaparami ng dalawang kumplikadong numero at isang dibisyon sa pamamagitan ng isang tunay na numero, ang parisukat ng ganap na halaga ng denominador.
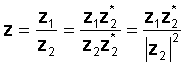
Halimbawa hayaan:
z1 = 3 - 4j at z2 = 2 + 3j
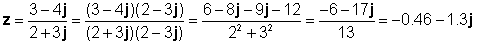
Suriin natin ang resulta sa TINA's Interpreter:
z1: = 3-4 * j
z2: = 2 + 3 * j
z1 / z2 = [- 461.5385m-1.3077 * j]
import math bilang m
import cmath bilang c
z1=kumplikado('3-4j')
z2=kumplikado('2+3j')
print("z1/z2="",z1/z2)
Dibisyon ng mga kumplikadong numero na ibinigay sa polar o exponential form
Upang maisagawa ang operasyon, hatiin ang mga ganap na halaga (magnitude) at ibawas ang anggulo ng denamineytor mula sa anggulo ng numerator. Hayaan:
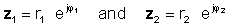
pagkatapos ay gamitin ang panuntunan ng dibisyon ng mga pag-exponential function
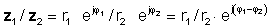
o sa polar form
z 1 / z2 = r1 / r2 ∠ φ 1- φ 2
Halimbawa, hayaan ang:
z 1 = 5 ∠ 30 ° at z 2 = 2 ∠ -60 °
pagkatapos
z 1 / z2 = 2.5 ∠ 90 °
o sa mga exponential at rectangular form
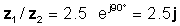
Suriin natin ang resulta sa TINA's Interpreter:
z1: = 5 * exp (j * degtorad (30))
z2: = 2 * exp (j * degtorad (-60))
z1 / z2 = [0 + 2.5 * j]
import math bilang m
import cmath bilang c
z1=5*(c.exp(complex(0,m.radians(30))))
z2=2*(c.exp(complex(0,m.radians(-60))))
print("z1/z2="",z1/z2)
Ang dibisyon ay malinaw na mas simple kapag ang mga numero ay nasa polar o exponential form.
Gayunpaman, kung ang mga kumplikadong numero ay ibinibigay sa hugis-parihaba form, dapat mong isaalang-alang ang pagsasagawa ng dibisyon nang direkta gamit ang kumplikadong paraan ng conjugate tulad ng ipinakita sa itaas, dahil may mga karagdagang hakbang kung i-convert mo ang mga numero sa form na polar bago paghatiin ang mga ito. Isa pang kadahilanan na dapat isaalang-alang ay kung nais mo ang mga sagot na nasa hugis-parihaba form o sa polar / exponential form. Halimbawa, kung ang dalawang numero ay nasa hugis-parihaba na form, ngunit nais mo ang kanilang quient sa polar form, makatuwiran na mai-convert kaagad ito at pagkatapos ay hatiin ang mga ito.
Ngayon ipaalam sa amin ilarawan ang paggamit ng mga kumplikadong mga numero sa pamamagitan ng higit pang mga numerical problema. Gaya ng dati, susuriin namin ang aming mga solusyon gamit ang TINA's Interpreter. Ang interpreter ay gumagana sa radians, ngunit ito ay may standard na mga pag-andar para sa conversion ng radians sa grado o vice-versa.
Halimbawa 1 Hanapin ang representasyon ng polar:
z = 12 - j 48
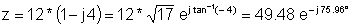
z: = 12-j * 48;
abs (z) = [49.4773]
arc (z) = [- 1.3258]
radtodeg (arc (z)) = [- 75.9638]
import math bilang m
import cmath bilang c
z=12-complex(48j)
print("abs(z)="",abs(z))
print("arc(z)="",c.phase(z))
print("degrees(arc(z))="",m.degrees(c.phase(z)))
Halimbawa 2 Hanapin ang hugis na parihaba:
z = 25 e j 125 °
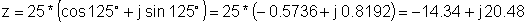
z: = 25 * exp (j * (degtorad (125)));
z = [- 14.3394 + 20.4788 * j]
Re (z) = [- 14.3394]
Im (z) = [20.4788]
import math bilang m
import cmath bilang c
z=25*c.exp(complex(0,m.radians(125)))
print("z="",z)
print("real(z)="",z.real)
print("imag(z)="",z.imag)
Halimbawa 3 Hanapin ang kinatawan ng polar ng sumusunod na mga kumplikadong numero:
z 1 = 12 + j 48 z2 = 12 - j48 z3= -12 + j 48 z4= -12 - j 48
Ang ganap na mga halaga ng lahat ng apat na numero ay pareho dahil ang ganap na halaga ay independiyente sa mga palatandaan. Tanging ang mga anggulo ang magkakaiba.
z1: = 12 + j * 48;
abs (z1) = [49.4773]
Arc (z1) = [1.3258]
radtodeg (Arc (z1)) = [75.9638]
z2: = 12-j * 48;
abs (z2) = [49.4773]
Arc (z2) = [- 1.3258]
radtodeg (Arc (z2)) = [- 75.9638]
z3: = - 12 + j * 48;
abs (z3) = [49.4773]
Arc (z3) = [1.8158]
radtodeg (Arc (z3)) = [104.0362]
z4: = - 12-j * 48:
abs (z4) = [49.4773]
Arc (z4) = [- 1.8158]
radtodeg (Arc (z4)) = [- 104.0362]
import math bilang m
import cmath bilang c
z1=kumplikado('12+48j')
print(“abs(z1)=",abs(z1))
print(“arc(z1)=",c.phase(z1))
print(“degrees(arc(z1))=”,m.degrees(c.phase(z1)))
z2=kumplikado('12-48j')
print(“abs(z2)=",abs(z2))
print(“arc(z2)=",c.phase(z2))
print(“degrees(arc(z2))=”,m.degrees(c.phase(z2)))
z3=kumplikado('-12+48j')
print(“abs(z3)=",abs(z3))
print(“arc(z3)=",c.phase(z3))
print(“degrees(arc(z3))=”,m.degrees(c.phase(z3)))
z4=kumplikado('-12-48j')
print(“abs(z4)=",abs(z4))
print(“arc(z4)=",c.phase(z4))
print(“degrees(arc(z4))=”,m.degrees(c.phase(z4)))
Ang pag-andar ng TINA () na function ay tinutukoy ang anggulo ng anumang kumplikadong numero, awtomatikong inilalagay ito nang tama sa isa sa apat na quadrant.
Mag-ingat, gayunpaman, gamit ang kulay-balat-1 pagpapaandar upang hanapin ang anggulo, dahil nililimitahan ito sa pagbalik ng mga anggulo sa una at ika-apat na quadrants (–90 °φ<90 °).
Dahil sa z1 ay matatagpuan sa unang kuwadrante ng sistema ng coordinate, ang pagkalkula ay:
α 1 = tan-1(48 / 12) = tan-1(4) = 75.96 °
Dahil sa z4 ay matatagpuan sa ikatlong kuwadrante ng sistema ng coordinate, tan-1hindi tama ang pagbalik ng anggulo. Ang pagkalkula ng anggulo ay:
α 4 = 180 ° + 75.96 ° = 255.96 ° o -360 ° + 255.96 ° = - 104.04 °, na kapareho ng kinakalkula ng TINA.
z2 ay matatagpuan sa ika-apat na kuwadrante ng sistema ng coordinate Ang pagkalkula ng anggulo ay:
α 2 = tan-1(-48 / 12) = tan-1(-4) = -75.96 °
z3, gayunpaman, ay nasa 2nd quadrant ng sistema ng coordinate, kaya kulay-balat-1 ay hindi tama ang ibalik ang anggulo. Ang pagkalkula ng anggulo ay:
α 3 = 180 ° -75.96 ° = 104.04 °.
Halimbawa 4 Mayroon kaming dalawang kumplikadong numero: z1= 4 - j 6 at z2 = 5 ej45 ° .
Mahanap z3 = z1 + z2; z4 = z1 - z2; z5 = z1 * z2; z6 = z1 / z2
Una naming lutasin ang problema gamit ang TINA's Interpreter
{Solusyon ng Interpreter ni TINA} |
Pansinin kung paano hawakan ng TINA nang walang kahirap-hirap ang dalawang kumplikadong numero na ibinigay sa iba't ibang anyo.
Ang solusyon ay mas kumplikado nang wala ang tagasalin. Sa gayon maaari nating ihambing ang iba't ibang mga pamamaraan ng pagpaparami at paghahati, una natin matukoy ang polar form ng z1 at ang hugis-parihaba na anyo ng z2 .
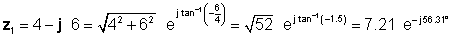
Susunod, nakita namin ang apat na mga solusyon gamit ang pinakamadaling mga form: hugis-parihaba para sa karagdagan at pagbabawas, at exponential para sa pagpaparami at paghahati:
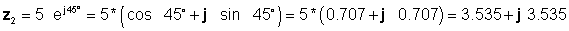
z 3 = z1 + z2 = 4 - j 6 + 3.535 + j 3.535 = 7.535 - j2.465
z 4 = z1 - z2 = 4 - j 6 - 3.535 - j 3.535 = 0.465 - j9.535
z 5 = z1 * z2 = 7.21 * 5 * ej(-56.31 ° + 45 °) = 36.05 e -j11.31 ° = 36.03 * (cos (-11.31 °) +j* kasalanan (-11.31 °))
z 5 = 35.33 - j 7.07
z 6 = z1/z2= (7.21 / 5) * e j (-56.31 ° -45 °) = 1.442 e - j 101.31 ° = 1.442 (cos (-101.31 °) +j* kasalanan (-101.31 °))
z 6 = -0.2828 - j 1.414
na sumasang-ayon sa mga resulta na nakuha sa TINA Interpreter.
Ang pagpaparami ay isinasagawa sa pormang hugis-parihaba:
z 5 =z1*z2 = (4-j6) * 3.535 * (1 +j) = 7.07 * (2-j3) * (1 +j) = 7.07 * (2-j3+j2 + 3) = 7.07 * (5-j) = 35.35-j7.07
Sa wakas ang dibisyon ay isinasagawa sa hugis-parihaba na anyo:
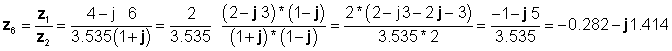
na sumang-ayon sa mga nakaraang resulta.
