 Натисніть або торкніться прикладної схеми нижче, щоб викликати TINACloud і вибрати режим інтерактивного постійного струму для аналізу в Інтернеті.
Натисніть або торкніться прикладної схеми нижче, щоб викликати TINACloud і вибрати режим інтерактивного постійного струму для аналізу в Інтернеті. Отримайте низький доступ до TINACloud для редагування прикладів або створення власних схем
У цій та наступних розділах ми представимо дуже важливу тему: AC або змінного струму. Назва змінного струму не дуже точна і зазвичай охоплює схеми з синусоїдальними напругами і струмами; однак змінного струму може також означати будь-яка довільна форма струму. Важливість змінної напруги полягає в тому, що цей тип напруги використовується для основного джерела електричної енергії в будинках і промисловості по всьому світу. Він також є основою для багатьох електронних, телекомунікаційних та промислових застосувань.
Для обробки синусоїдальних форм хвиль і пов'язаних з ними схем ми будемо використовувати простий і елегантний метод, який називається методом фазорів. Фазори засновані на властивостях комплексних чисел, які ідеально підходять для представлення синусоїдальних величин. У цьому розділі ми підсумуємо основні факти про складні числа та їхні операції. Ми також покажемо, як інтерпретатор TINA дозволяє легко робити розрахунки з комплексними числами.
Комплексні числа складаються з двох частин: a реальна частина (x), що є дійсним числом, і так званим уявна частина (y), що є дійсним числом, помноженим на 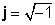
z = x + jy
де 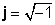
Приклади складних номерів:
z 1 = 1 + j
z 2 = 4-2 j
z 3 = 3- 5j
Складні числа спочатку були введені у XVII столітті для відображення коренів многочленів, які не могли бути представлені лише реальними числами. Наприклад, коріння рівняння х2 + 2x + 2 = 0 можна описати лише як 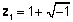
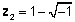
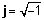
Геометричне представлення комплексних чисел
Прямокутна форма
Оскільки складне число завжди можна розділити на його реальну та складну частини, ми можемо представляти складне число у вигляді точки на двовимірній площині. Реальна частина комплексного числа - це проекція точки на реальну вісь, а уявна частина числа - проекція на уявну вісь. Коли складне число представлено як суму реальної та уявної частин, ми говоримо, що воно є прямокутний or алгебраїчна форма.
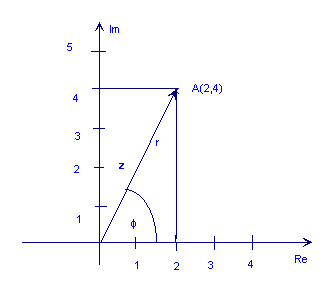
Наступний малюнок показує комплексне число z = 2 + 4j
Полярна і експоненціальна форма
Як видно з малюнка вище, точка А також може бути представлена довжиною стрілки, r (також називається абсолютним значенням, величиною або амплітудою) та його кутом (або фазою), φ відносно проти годинникової стрілки до позитивної горизонтальної осі. Це полярний форма комплексного числа. Він позначається як r ∠ φ.
Наступний крок є дуже важливим. Комплексне число в полярній формі також можна записати експонентний форма:
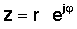
Цей простий вираз відрізняється тим, що він має уявне число в експоненті замість звичайного дійсного числа. Цей складний показник поводиться дуже інакше від експоненціальної функції з реальним аргументом. У той час як ex швидко зростає за величиною для збільшення x> 0 і зменшується для x <0, функція 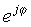
Формула Ейлера забезпечує уніфікуючу зв'язок між прямокутними, полярними і експоненціальними формами комплексних чисел:
z = x + jy = re jφ = r (cos φ + j гріх φ )
де 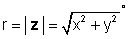
та φ = загар-1 (y / x).
Для нашого прикладу вище, z = 2 + 4j:
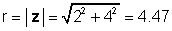
φ = загар-1 (4 / 2) = 63.4 °
отже 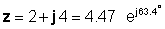
Або навпаки:
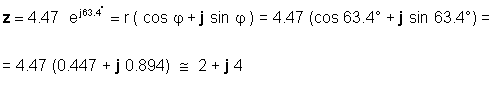
Вам потрібно буде вміло використовувати обидві форми, залежно від програми. Наприклад, додавання або віднімання, очевидно, простіше зробити, коли числа мають прямокутну форму, тоді як множення і ділення легше зробити, коли числа знаходяться в експоненціальній формі.
Операції з комплексними числами
Операції, які можна виконати зі складними числами, аналогічні операціям для дійсних чисел. Правила та деякі нові визначення наведені нижче.
Операції з j
Операції з j просто випливати з визначення уявної одиниці,


Щоб мати можливість працювати швидко і точно, ви повинні запам'ятати ці правила:
j 2 = -1
j 3 =-j
j 4 =1
1/j = -j
j2 = -1 просто випливає з визначення 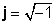
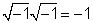
Для 1 /j, ми помножимо 1 /jby j / j = 1 і отримати j/ (jj) = j / (- 1) = -j.
Комплексний кон'югат
Комплексний кон'югат комплексного числа легко виводиться і є досить важливим. Щоб отримати складне спряження складного числа в прямокутній формі, просто змініть знак уявної частини. Щоб зробити це для числа в експоненційній формі, змініть знак кута комплексного числа, зберігаючи при цьому його абсолютне значення.
Комплексний кон'югат комплексного числа z часто позначається z*.
Дано комплексне число z= a + jb, його комплексний кон'югат z*= a– jb.
If z дається в експоненціальній формі, 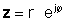
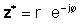
Використовуючи вищевикладені визначення, неважко бачити, що комплексне число, помножене на його складне спряжене, дає квадрат абсолютного значення комплексного числа:
zz* = r2 = a2 + b2
Також, шляхом додавання або віднімання будь-якого комплексного числа і його сполученого, отримуємо наступні співвідношення:
z + z * = 2a
отже
Re (z) = a = ( z + z * ) / 2
Аналогічно:
z - z * =j2b
отже
Im (z) = b = ( z -z * ) / 2j
Доказ:
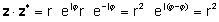
або множення реальної і уявної частин і використання j2= -1
zz* = (a + jб) (a - jb) = a2+a jб - а jб - jbjb = a2j2 = a2 + b2
z + z* = a + jb + a - jb = 2a
z - z*= a + jb - a + jb =j2b
Числові приклади:
У прямокутній формі:
z = 3 + j4
z* = 3– j4
zz * = 9 + 16 = 25
У полярній формі
z = 5 ∠ 53.13 °
z * = 5 ∠ - 53.13 °
У експоненціальній формі:
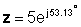
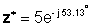
Додавання і віднімання
Додавання і віднімання складних чисел просте - нам потрібно лише додати реальні та уявні частини окремо. Наприклад, якщо
z1 = 3 - 4j та z2 = 2 + 3j
потім
z1 + z2 = 3 - 4j + 2 + 3j = 3 + 2 - 4j + 3j = 5 - j
z1 - z2 = 3 - 4j - 2 - 3j = 3 - 2 - 4j - 3j = 1 - j7
Очевидно, що для цих операцій нам слід використовувати прямокутну форму. Якщо числа задані в експоненціальній або полярній формі, ми повинні перетворити їх спочатку в прямокутну форму, використовуючи формулу Ейлера, як було зазначено раніше.
Множення
Існує два методи множення комплексних чисел -
Множення складних чисел дано в прямокутній формі
Щоб здійснити операцію, просто помножте реальну та уявну частини одного числа по черзі на реальну та уявну частини іншого числа та використовуйте тотожність j2 = -1.
z1z2 = (a1 + jb1) (a2 + jb2) = a1 a2 + jb1a2+ jb2a1 - б1b2 = a1 a2- б1b2 + j(b1a2+ jb2a1)
Коли комплексні числа наводяться чисельно, не потрібно використовувати формулу вище. Наприклад, нехай
z1 = 3 - 4j та z2 = 2 + 3j
При прямому множенні компонентів:
z1z2 = (3 - 4j) (2 + 3j) = 6-8j +9j + 12 = 18 + j
або за допомогою формули: z1z2 = a1 a2- б1b2 + j(b1a2+ b2a1)
z1z2 = 6 + 12 + j (-8 + 9) = 18 + j
Ми вважаємо, що ви, скоріше за все, зробите помилку, якщо ви використовуєте формулу, ніж якщо безпосередньо помножити компоненти.
z1: = 3-4 * j
z2: = 2 + 3 * j
z1 * z2 = [18 + 1 * j]
імпортувати математику як m
імпортувати cmath як c
z1=complex('3-4j')
z2=complex('2+3j')
print(“z1*z2=”,z1*z2)
Множення складних чисел задається в полярній або експоненціальній формі
Щоб виконати цю операцію, помножте абсолютні значення і додайте кути двох комплексних чисел. Дозволяє:
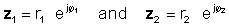
Потім за допомогою правила множення експоненційних функцій:
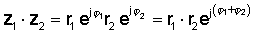
або в полярній формі
z1 z2 = r1 r2 ∠ φ1 + φ2
Примітка: Ми вже використовували це правило, коли розраховували zz *вище. Оскільки кут сполучника має протилежний знак початкового кута, складне число, помножене на власний сполучник, завжди є дійсним числом; а саме квадрат його абсолютної величини: zz * = r2
Наприклад, нехай:
z1 = 5 ∠ 30 ° і z2 = 4 ∠ -60 °
потім
z1z2 = 20 ∠ -30 °
або в експоненціальній формі
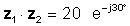
Множення, очевидно, простіше, коли числа знаходяться в полярній або експоненціальній формі.
Однак, якщо складні числа задані у прямокутній формі, слід розглянути можливість виконання множення безпосередньо, як показано вище, оскільки є додаткові кроки, якщо ви перетворите числа на полярну форму, перш ніж помножувати їх. Ще один фактор, який слід враховувати, чи потрібно, щоб відповіді були у прямокутній формі або в полярній / експоненціальній формі. Наприклад, якщо ці два числа мають прямокутну форму, але ви хочете, щоб їх добуток був у полярній формі, має сенс їх перетворити відразу, а потім помножити.
Роздільна
Існує два методи ділення комплексних чисел–
Поділ комплексних чисел дається в прямокутній формі
Для проведення операції помножте чисельник та знаменник на сполучник знаменника. Знаменник стає реальним числом, а ділення зводиться до множення двох складних чисел і ділення на реальне число, квадрат абсолютного значення знаменника.
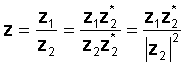
Наприклад:
z1 = 3 - 4j та z2 = 2 + 3j
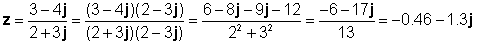
Давайте перевіримо цей результат з Інтерпретатором TINA:
z1: = 3-4 * j
z2: = 2 + 3 * j
z1 / z2 = [- 461.5385m-1.3077 * j]
імпортувати математику як m
імпортувати cmath як c
z1=complex('3-4j')
z2=complex('2+3j')
print(“z1/z2=”,z1/z2)
Поділ комплексних чисел дається в полярній або експоненціальній формі
Щоб виконати операцію, поділіть абсолютні значення (величини) і відняти кут знаменника від кута чисельника. Дозволяє:
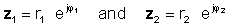
потім використовують правило розподілу експоненційних функцій
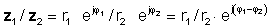
або в полярній формі
z 1 / z2 = r1 / r2 ∠ φ 1- φ 2
Наприклад, нехай:
z 1 = 5 ∠ 30 ° і z 2 = 2 ∠ -60 °
потім
z 1 / z2 = 2.5 ∠ 90 °
або в експоненціальних і прямокутних формах
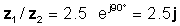
Давайте перевіримо цей результат з Інтерпретатором TINA:
z1: = 5 * exp (j * degtorad (30))
z2: = 2 * exp (j * degtorad (-60))
z1 / z2 = [0 + 2.5 * j]
імпортувати математику як m
імпортувати cmath як c
z1=5*(c.exp(complex(0,m.radians(30))))
z2=2*(c.exp(complex(0,m.radians(-60))))
print(“z1/z2=”,z1/z2)
Ділення, очевидно, простіше, коли числа знаходяться в полярній або експоненціальній формі.
Однак якщо складні числа задані у прямокутній формі, слід розглянути можливість виконання ділення безпосередньо, використовуючи складний метод спряженого, як показано вище, оскільки є додаткові кроки, якщо ви перетворюєте числа в полярну форму, перш ніж ділити їх. Ще один фактор, який слід враховувати, чи потрібно, щоб відповіді були у прямокутній формі або в полярній / експоненціальній формі. Наприклад, якщо два числа мають прямокутну форму, але ви хочете, щоб їх коефіцієнт був у полярній формі, має сенс негайно їх перетворити, а потім розділити.
Тепер проілюструємо використання складних чисел більш чисельними проблемами. Як завжди, ми перевіримо наші рішення за допомогою інтерпретатора TINA. Інтерпретатор працює з радіанами, але він має стандартні функції для перетворення радіанів в градуси або навпаки.
Приклад 1 Знайти полярне зображення:
z = 12 - j 48
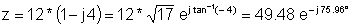
z: = 12-j * 48;
abs (z) = [49.4773]
arc (z) = [- 1.3258]
radtodeg (arc (z)) = [- 75.9638]
імпортувати математику як m
імпортувати cmath як c
z=12-комплекс (48j)
print(“abs(z)=”,abs(z))
print(“arc(z)=”,c.phase(z))
print(“degrees(arc(z))=”,m.degrees(c.phase(z)))
Приклад 2 Знайти прямокутне зображення:
z = 25 e j 125 °
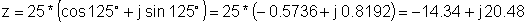
z: = 25 * exp (j * (дегональ (125)));
z = [- 14.3394 + 20.4788 * j]
Re (z) = [- 14.3394]
Im (z) = [20.4788]
імпортувати математику як m
імпортувати cmath як c
z=25*c.exp(complex(0,m.radians(125)))
print(“z=”,z)
print(“real(z)=”,z.real)
print(“imag(z)=”,z.imag)
Приклад 3 Знайти полярне представлення таких комплексних чисел:
z 1 = 12 + j 48 z2 = 12 - j48 z3= -12 + j 48 z4= -12 - j 48
Абсолютні значення всіх чотирьох чисел однакові, оскільки абсолютне значення не залежить від знаків. Тільки кути різні.
z1: = 12 + j * 48;
abs (z1) = [49.4773]
arc (z1) = [1.3258]
radtodeg (arc (z1)) = [75.9638]
z2: = 12-j * 48;
abs (z2) = [49.4773]
arc (z2) = [- 1.3258]
radtodeg (arc (z2)) = [- 75.9638]
z3: = - 12 + j * 48;
abs (z3) = [49.4773]
arc (z3) = [1.8158]
radtodeg (arc (z3)) = [104.0362]
z4: = - 12-j * 48:
abs (z4) = [49.4773]
arc (z4) = [- 1.8158]
radtodeg (arc (z4)) = [- 104.0362]
імпортувати математику як m
імпортувати cmath як c
z1=complex('12+48j')
print(“abs(z1)=”,abs(z1))
print(“arc(z1)=”,c.phase(z1))
print(“degrees(arc(z1))=”,m.degrees(c.phase(z1)))
z2=complex('12-48j')
print(“abs(z2)=”,abs(z2))
print(“arc(z2)=”,c.phase(z2))
print(“degrees(arc(z2))=”,m.degrees(c.phase(z2)))
z3=complex('-12+48j')
print(“abs(z3)=”,abs(z3))
print(“arc(z3)=”,c.phase(z3))
print(“degrees(arc(z3))=”,m.degrees(c.phase(z3)))
z4=complex('-12-48j')
print(“abs(z4)=”,abs(z4))
print(“arc(z4)=”,c.phase(z4))
print(“degrees(arc(z4))=”,m.degrees(c.phase(z4)))
Функція дуги () TINA визначає кут будь-якого складного числа, автоматично розміщуючи його правильно в одному з чотирьох квадрантів.
Проте будьте обережні, використовуючи загар-1 функція для знаходження кута, оскільки вона обмежена повертаючими кутами лише в першому та четвертому квадрантах (–90 °φ<90 °).
З z1 розташований у першому квадранті системи координат, розрахунок:
α 1 = загар-1(48 / 12) = загар-1(4) = 75.96 °
З z4 розташований в третьому квадранті системи координат, tan-1не повертає правильний кут. Розрахунок кута:
α 4 = 180 ° + 75.96 ° = 255.96 ° або -360 ° + 255.96 ° = - 104.04 °, що є тим самим, що розрахували за TINA.
z2 розташований у четвертому квадранті системи координат Розрахунок кута:
α 2 = загар-1(-48 / 12) = загар-1(-4) = -75.96 °
z3, однак знаходиться в квадранті 2nd системи координат, тому загар-1 не повертає правильний кут. Розрахунок кута:
α 3 = 180 ° -75.96 ° = 104.04 °.
Приклад 4 У нас є два складних числа: z1= 4 - j 6 і z2 = 5 ej45 ° .
знайти z3 = z1 + z2; z4 = z1 - z2; z5 = z1 * z2; z6 = z1 / z2
Спочатку ми вирішимо проблему за допомогою інтерпретатора TINA
{Рішення перекладача TINA} |
Зверніть увагу на те, як TINA без зусиль обробляє два складних числа, що подаються в різних формах.
Рішення складніше без перекладача. Щоб ми могли порівняти різні методи множення і ділення, спочатку визначимо полярну форму z1 і прямокутної форми z2 .
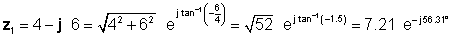
Далі ми знаходимо чотири рішення спочатку, використовуючи найпростіші форми: прямокутні для додавання та віднімання та експоненціальні для множення та ділення:
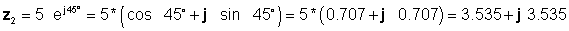
z 3 = z1 + z2 = 4 - j 6 + 3.535 + j 3.535 = 7.535 - j2.465
z 4 = z1 - z2 = 4 - j 6 - 3.535 - j 3.535 = 0.465 - j9.535
z 5 = z1 * z2 = 7.21 * 5 * ej(-56.31 ° + 45 °) = 36.05 e -j11.31 ° = 36.03 * (cos (-11.31 °) +j* sin (-11.31 °))
z 5 = 35.33 - j 7.07
z 6 = z1/z2= (7.21 / 5) * e j (-56.31 ° -45 °) = 1.442 e - j 101.31 ° = 1.442 (cos (-101.31 °) +j* sin (-101.31 °))
z 6 = -0.2828 - j 1.414
які погоджуються з результатами, отриманими з інтерпретатором TINA.
Множення здійснюється в прямокутній формі:
z 5 =z1*z2 = (4-j6) * 3.535 * (1 +j) = 7.07 * (2-j3) * (1 +j) = 7.07 * (2-j3+j2 + 3) = 7.07 * (5-j) = 35.35-j7.07
Нарешті поділ здійснюється в прямокутній формі:
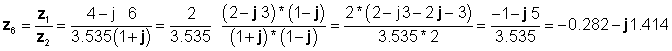
які погоджуються з попередніми результатами.

