 TINACloud-i çağırmaq üçün aşağıdakı nümunəvi sxemləri vurun və ya vurun və İnteraktiv DC rejimini Online onları təhlil etmək üçün seçin.
TINACloud-i çağırmaq üçün aşağıdakı nümunəvi sxemləri vurun və ya vurun və İnteraktiv DC rejimini Online onları təhlil etmək üçün seçin. TINACloud-a nümunələri düzəltmək və öz sxemlərinizi yaratmaq üçün aşağı qiymətə çıxın
Bu və növbəti fəsillərdə çox vacib bir mövzunu təqdim edəcəyik: AC və ya Alternativ Akım. Adı alternativ cərəyan çox dəqiq deyil və adətən sinusoidal gərginlik və cərəyanlar olan dövrləri əhatə edir; lakin alternativ cərəyan hər hansı bir özbaşına cərəyan edən cərəyan dalğası deməkdir. AC gərginliyin əhəmiyyəti bu cür gərginliyin evlərdə və sənayedə bütün dünyada əsas elektrik enerjisi mənbəyi üçün istifadə edilməsidir. Bu, bir çox elektronika, telekommunikasiya və sənaye tətbiqlərinin əsasını təşkil edir.
Sinusoidal dalğa formasını və onlarla əlaqəli sxemləri idarə etmək üçün, biz phasors metodu adlanan sadə və zərif bir metoddan istifadə edəcəyik. Fasorlar sinusoidal miqdarları təmsil etmək üçün ideal olan kompleks ədədlərin xüsusiyyətlərinə əsaslanır. Bu fəsildə kompleks ədədlər və onların əməliyyatları barədə əsas faktları ümumiləşdirəcəyik. Tina'nın tərcüməçisinin kompleks nömrələri ilə hesablamaları asanlaşdırdığını göstərəcəyik.
Kompleks nömrələr iki hissədən ibarətdir: a real hissəsi (x), bir real sayda olan və bir sözlə xəyali hissəsidir (y), bu da bir çox sayda bir ədəddir 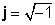
z = x + jy
hara 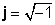
Kompleks nömrələrin nümunələri:
z 1 = 1 + j
z 2 = 4-2 j
z 3 = 3- 5j
Kompleks ədədlər əvvəlcə XVII əsrdə tək həqiqi ədədlərlə ifadə edilə bilməyən çoxbucaqlıların köklərini təmsil etmək üçün təqdim edilmişdir. Məsələn, x tənliyinin kökləri2 + 2x + 2 = 0 kimi yalnız təsvir edilə bilər 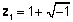
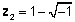
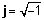
Kompleks nömrələrin həndəsi təsvirləri
Düzbucaqlı forma
Kompleks bir nömrə həmişə həqiqi və mürəkkəb hissələrinə ayrıla bildiyindən kompleks bir ədədi iki ölçülü bir müstəvidə bir nöqtə olaraq təmsil edə bilərik. Mürəkkəb bir ədədin həqiqi hissəsi nöqtənin həqiqi oxa doğru proyeksiyası, ədədin xəyali hissəsi isə xəyali oxa proyeksiyadır. Mürəkkəb bir sıra həqiqi və xəyali hissələrin cəmi kimi təmsil edildiyi zaman içindəyik düzbucaqlı or cəbri forması.
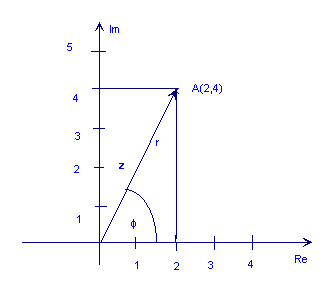
Aşağıdakı rəqəm kompleks sayını göstərir z = 2 + 4j
Polar və eksponent forması
Yuxarıdakı şəkildən göründüyü kimi, A nöqtəsi oxun uzunluğu ilə də göstərilə bilər; r (mütləq dəyər, ölçü və ya amplituda da deyilir) və bucağı (və ya fazası), φ əks üfüqi oxa qarşı əks istiqamətdə. Bu qütb kompleks ədədin forması. R ∠ kimi qeyd olunur φ.
Növbəti addım çox vacibdir. Qütb şəklində bir kompleks ədəd də yazıla bilər exponential form:
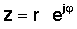
Bu sadə ifadə fərqlidir ki, adi həqiqi nömrə əvəzinə eksponentdə xəyali bir nömrəyə sahibdir. Bu mürəkkəb eksponensial eksponensial funksiyadan həqiqi bir dəlil ilə çox fərqli davranır. E isəx x> 0 artması üçün böyüklükdə sürətlə böyüyür və x <0 üçün azalır, funksiyası 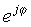
Euler formulası kompleks ədədlərin düzbucaqlı, qütblü və eksponent formaları arasında birləşən əlaqə yaradır:
z = x + jy = re jφ = r (cos φ + j günah φ )
hara 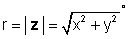
və φ = tan-1 (y / x).
Yuxarıdakı nümunə üçün, z = 2 + 4j:
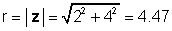
φ = tan-1 (4 / 2) = 63.4 °
Buna görə 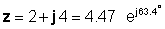
Və ya əksinə:
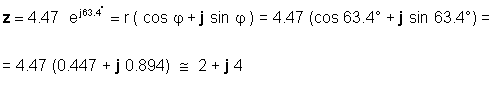
Tətbiqdən asılı olaraq hər iki formanı istifadə etməkdə usta olmalısınız. Məsələn, ədədlər düzbucaqlı formada olduqda əlavə və ya toplama işlərini etmək asan olar, ədədlər eksponent formada olduqda vurma və bölmək daha asandır.
Kompleks nömrələri olan əməliyyatlar
Kompleks ədədlərlə edilə bilən əməliyyatlar həqiqi ədədlər üçün edilən əməliyyatlara bənzəyir. Qaydalar və bəzi yeni təriflər aşağıda ümumiləşdirilmişdir.
J ilə əməliyyatlar
Əməliyyatlar j sadəcə xəyali vahidin tərifindən,


Hızlı və dəqiq çalışa bilmək üçün bu qaydaları yadda saxlamalısınız:
j 2 = -1
j 3 =-j
j 4 =1
1/j = -j
j2 = -1 sadəcə tərifindən gəlir 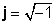
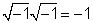
1 /j, biz 1 /jby j / j = 1 və get j/ (jj) = j / (- 1) = -j.
Kompleks birləşmə
Mürəkkəb sayının kompleks birləşməsi asanlıqla əldə edilir və olduqca vacibdir. Mürəkkəb sayının düzbucaqlı formada kompleks birləşməsini əldə etmək üçün sadəcə xəyali hissənin əlamətini dəyişdirin. Ustel formada bir sıra üçün bunu mütləq dəyərini eyni saxlayarkən kompleks sayının işarəsini dəyişdirin.
Kompleks sayının kompleks birləşməsi z tez-tez göstərilir z*.
Kompleks sayını nəzərə alaraq z= a + jb, kompleksi birləşmədir z*= a- jb.
If z eksponent formada verilir, 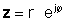
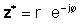
Yuxarıdakı anlayışlardan istifadə edərək kompleks birləşmənin çarpan bir kompleks sayı kompleks sayının mütləq dəyərinin kvadratını verir:
zz* = r2 = a2 + b2
Ayrıca, hər hansı bir kompleks sayı və onun birləşməsini əlavə etmək və ya çıxarmaqla aşağıdakı əlaqələri alırıq:
z + z * = 2a
Buna görə
Re (z) = a = ( z + z * ) / 2
Oxşar:
z - z * =j2b
Buna görə
Im (z) = b = ( z -z * ) / 2j
Proof:
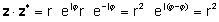
və ya real və xəyali hissələrə çarpar və istifadə edir j2= -1
zz* = (a + jb) (a - jb) = a2+a jb - a jb - jbjb = a2j2 = a2 + b2
z + z* = a + jb + a - jb = 2a
z - z*= a + jb - a + jb =j2b
Nümerik nümunələr:
Düzbucaqlı formada:
z = 3 + j4
z* = 3- j4
zz * = 9 + 16 = 25
Qütb şəklində
z = 5 ∠ 53.13 °
z * = 5 ∠- 53.13 °
Eksponent formada:
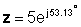
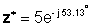
Əlavə və toplama işarəsi
Mürəkkəb ədədlərin əlavə və ayrılması düzdür - yalnız həqiqi və xəyali hissələri ayrıca əlavə etməliyik. Məsələn, əgər
z1 = 3 - 4j və z2 = 2 + 3j
sonra
z1 + z2 = 3 - 4j + 2 + 3j = 3 + 2 - 4j + 3j = 5 - j
z1 - z2 = 3 - 4j - 2 - 3j = 3 - 2 - 4j - 3j = 1 - j7
Aydındır ki, bu əməliyyatlar üçün düzbucaqlı formadan istifadə etməliyik. Ədədlər eksponensial və ya qütb şəklində verilsə, əvvəllər verildiyi kimi əvvəlcə Euler düsturundan istifadə edərək onları düzbucaqlı formaya çevirməliyik.
Vurma
Mürəkkəb ədədi vurmağın iki üsulu var -
Dikdəyiş şəklində verilmiş kompleks nömrələrin çarpılması
Əməliyyatı həyata keçirmək üçün bir nömrənin həqiqi və xəyali hissələrini digər nömrənin həqiqi və xəyali hissələrinə növbə ilə çoxaltmaq və şəxsiyyətini istifadə etmək kifayətdir j2 = -1.
z1z2 = (a1 + jb1) (a2 + jb2) = a1 a2 + jb1a2+ jb2a1 - b1b2 = a1 a2- b1b2 + j(b1a2+ jb2a1)
Kompleks nömrələr sayca verildikdə, yuxarıdakı formulun istifadə edilməsinə ehtiyac yoxdur. Məsələn, imkan verək
z1 = 3 - 4j və z2 = 2 + 3j
Komponentlərin birbaşa çarpılması ilə:
z1z2 = (3 - 4j) (2 + 3j) = 6-8j +9j + 12 = 18 + j
və ya formula istifadə: z1z2 = a1 a2- b1b2 + j(b1a2+ B2a1)
z1z2 = 6 + 12 + j (-8 + 9) = 18 + j
Formulları birbaşa çarpdığınızdan daha çox istifadə etsəniz səhv etmək ehtimalı daha çox olduğunuzu düşünürük.
z1: = 3-4 * j
z2: = 2 + 3 * j
z1 * z2 = [18 + 1 * j]
m kimi riyaziyyatı idxal edin
c kimi idxal cmath
z1=kompleks('3-4j')
z2=kompleks('2+3j')
çap(“z1*z2=”,z1*z2)
Qütb və ya eksponent formada verilmiş kompleks ədədlərin çarpılması
Bu əməliyyatı yerinə yetirmək üçün mütləq dəyərləri vurun və iki kompleks ədədin açılarını əlavə edin. Qoyun:
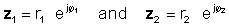
Sonra eksponent funksiyaların vurma qaydasını istifadə edərək:
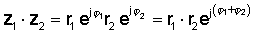
və ya qütb şəklində
z1 z2 = r1 r2 ∠ φ1 + φ2
Qeyd: Hesabladığımız zaman bu qaydanı istifadə etdik zz *yuxarıda. Konyugatın bucağı orijinal bucağın əks işarəsinə malik olduğundan, öz konyugatına vurulmuş mürəkkəb bir ədəd həmişə həqiqi bir ədəddir; yəni mütləq dəyərinin kvadratıdır: zz * = r2
Məsələn:
z1 = 5 ∠ 30 ° və z2 = 4 ∠ -60 °
sonra
z1z2 = 20 ∠ -30 °
və ya exponential formada
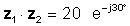
Nömrələr polar və ya eksponent formada olduğunda çarpmanın açıq-aydın olması çox asandır.
Ancaq mürəkkəb ədədlər düzbucaqlı formada verilmişdirsə, vurmağın birbaşa yuxarıda göstərildiyi kimi aparılmasını düşünməlisiniz, çünki nömrələri çoxaltmadan əvvəl qütb formasına çevirsəniz əlavə addımlar var. Diqqət yetirməli başqa bir amil, cavabların düzbucaqlı və ya qütb / eksponent şəklində olmasını istəməyinizdir. Məsələn, iki ədəd düzbucaqlı formadadır, lakin məhsullarını qütb şəklində istəsəniz, dərhal onları çevirmək və sonra çoxaltmaq məna verir.
Bölmə
Mürəkkəb ədədlərin bölünməsinin iki üsulu var -
Dikdörtgen şəklində verilmiş kompleks nömrələrin bölüşdürülməsi
Əməliyyatı yerinə yetirmək üçün ədədi və məxrəci məxrəcin birləşməsi ilə vurun. Məxrəc həqiqi bir nömrəyə çevrilir və bölünmə iki mürəkkəb ədədin çoxalmasına və həqiqi bir ədədin, məxrəcin mütləq dəyərinin kvadratına bölünməsinə endirilir.
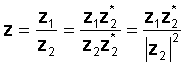
Məsələn:
z1 = 3 - 4j və z2 = 2 + 3j
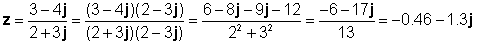
Bu nəticə TINA-nın Tərcüməçi ilə yoxlayın:
z1: = 3-4 * j
z2: = 2 + 3 * j
z1 / z2 = [- 461.5385m-1.3077 * j]
m kimi riyaziyyatı idxal edin
c kimi idxal cmath
z1=kompleks('3-4j')
z2=kompleks('2+3j')
çap(“z1/z2=”,z1/z2)
Qütb və ya eksponent formada verilmiş kompleks nömrələrin bölüşdürülməsi
Əməliyyatın həyata keçirilməsi üçün mütləq dəyərləri bölməyin və nişanlanmanın açıını ədədi açısından çıxarın. Qoyun:
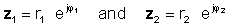
sonra exponential funksiyaların bölünməsi qayda istifadə
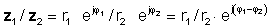
və ya qütb şəklində
z 1 / z2 = r1 / r2 ∠ φ 1- φ 2
Məsələn:
z 1 = 5 ∠ 30 ° və z 2 = 2 ∠ -60 °
sonra
z 1 / z2 = 2.5 ∠ 90 °
və ya eksponent və düzbucaqlı formalarda
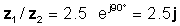
Bu nəticə TINA-nın Tərcüməçi ilə yoxlayın:
z1: = 5 * exp (j * degtorad (30))
z2: = 2 * exp (j * degtorad (-60))
z1 / z2 = [0 + 2.5 * j]
m kimi riyaziyyatı idxal edin
c kimi idxal cmath
z1=5*(c.exp(kompleks(0,m.radian(30))))
z2=2*(c.exp(kompleks(0,m.radian(-60))))
çap(“z1/z2=”,z1/z2)
Rəqəmlər qütblü və ya eksponensial formada olduqda açıq şəkildə daha sadə olur.
Ancaq kompleks nömrələr düzbucaqlı formada verilmişdirsə, yuxarıda göstərildiyi kimi kompleks birləşmə metodundan istifadə edərək bölməni birbaşa yerinə yetirməyi düşünməlisiniz, çünki nömrələri bölmədən əvvəl qütb formasına çevirsəniz əlavə addımlar var. Diqqət yetirməli başqa bir amil, cavabların düzbucaqlı və ya qütb / eksponent şəklində olmasını istəməyinizdir. Məsələn, iki ədəd düzbucaqlı formadadır, amma onların qütb şəklində verilməsini istəsəniz, onları dərhal çevirin və sonra bölün.
İndi kompleks ədədlərin daha çox ədədi problemlərlə istifadə edilməsini göstərək. Hər zamanki kimi, TINA-nın Tərcüməçi vasitəsi ilə həllərimizi yoxlayacağıq. Tərcüməçi radyanlarla işləyir, lakin radyanların dərəcəyə və ya əksinə çevrilməsinə dair standart funksiyaları vardır.
Məsələn 1 Qütb təmsilçisini tapın:
z = 12 - j 48
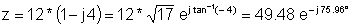
z: = 12-j * 48;
abs (z) = [49.4773]
arc (z) = [- 1.3258]
radtodeg (arc (z)) = [- 75.9638]
m kimi riyaziyyatı idxal edin
c kimi idxal cmath
z=12-kompleks(48j)
çap(“abs(z)=”,abs(z))
çap(“qövs(z)=”,c.faza(z))
çap("dərəcə(qövs(z))=",m.dərəcə(c.faza(z)))
Məsələn 2 Düzbucaqlı təsvirləri tapın:
z = 25 e j 125 °
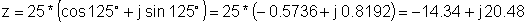
z: = 25 * exp (j * (degtorad (125)));
z = [- 14.3394 + 20.4788 * j]
Re (z) = [- 14.3394]
Im (z) = [20.4788]
m kimi riyaziyyatı idxal edin
c kimi idxal cmath
z=25*c.exp(kompleks(0,m.radian(125)))
çap (“z=”,z)
çap ("real(z)=",z.real)
çap ("imag(z)=",z.imag)
Məsələn 3 Aşağıdakı kompleks ədədlərin polar nümayəndəliyini tapın:
z 1 = 12 + j 48 z2 = 12 - j48 z3= -12 + j 48 z4= -12 - j 48
Bütün dörd ədədin mütləq dəyərləri eynidır, çünki mütləq dəyər işarələrdən asılı deyil. Yalnız açılar fərqlidir.
z1: = 12 + j * 48;
abs (z1) = [49.4773]
arc (z1) = [1.3258]
radtodeg (arc (z1)) = [75.9638]
z2: = 12-j * 48;
abs (z2) = [49.4773]
arc (z2) = [- 1.3258]
radtodeg (arc (z2)) = [- 75.9638]
z3: = - 12 + j * 48;
abs (z3) = [49.4773]
arc (z3) = [1.8158]
radtodeg (arc (z3)) = [104.0362]
z4: = - 12-j * 48:
abs (z4) = [49.4773]
arc (z4) = [- 1.8158]
radtodeg (arc (z4)) = [- 104.0362]
m kimi riyaziyyatı idxal edin
c kimi idxal cmath
z1=kompleks('12+48j')
çap(“abs(z1)=”,abs(z1))
çap(“qövs(z1)=”,c.faza(z1))
çap(“dərəcə(qövs(z1))=”,m.dərəcə(c.faza(z1)))
z2=kompleks('12-48j')
çap(“abs(z2)=”,abs(z2))
çap(“qövs(z2)=”,c.faza(z2))
çap(“dərəcə(qövs(z2))=”,m.dərəcə(c.faza(z2)))
z3=kompleks('-12+48j')
çap(“abs(z3)=”,abs(z3))
çap(“qövs(z3)=”,c.faza(z3))
çap(“dərəcə(qövs(z3))=”,m.dərəcə(c.faza(z3)))
z4=kompleks('-12-48j')
çap(“abs(z4)=”,abs(z4))
çap(“qövs(z4)=”,c.faza(z4))
çap(“dərəcə(qövs(z4))=”,m.dərəcə(c.faza(z4)))
TINA-nın qövs () funksiyası istənilən dördrəngdən birinə düzgün yerləşdirərək istənilən mürəkkəb ədədin bucağını təyin edir.
Ancaq tan istifadə edərək, diqqətli olun-1 bucağı tapmaq funksiyası, çünki yalnız birinci və dördüncü dörddə (-90 °) dönmə bucaqları ilə məhdudlaşır.φ<90 °).
Etibarən z1 koordinat sisteminin ilk kvadrantında yerləşir, hesablama edir:
α 1 = tan-1(48 / 12) = tan-1(4) = 75.96 °
Etibarən z4 koordinat sisteminin üçüncü quadrantında yerləşir-1bucaq düzgün qaytarır. Bucaq hesablanması:
α 4 = 180 ° + 75.96 ° = 255.96 ° və ya -360 ° + 255.96 ° = - 104.04 °, bu TINA tərəfindən hesablanmışdır.
z2 koordinat sisteminin dördüncü kvadratında yerləşir. Açıq hesablama:
α 2 = tan-1(-48 / 12) = tan-1(-4) = -75.96 °
z3, lakin koordinat sisteminin 2nd quadrantında, yəni tan-1 bucağı düzgün qaytarmır. Bucaq hesablanması:
α 3 = 180 ° -75.96 ° = 104.04 °.
Məsələn 4 İki kompleks ədəd var: z1= 4 - j 6 və z2 = 5 ej45 ° .
SİZİN ÜÇÜN MÜKEMMEL YERİ TAPIN z3 = z1 + z2; z4 = z1 - z2; z5 = z1 * z2; z6 = z1 / z2
Əvvəlcə TINA'nın Tərcüməçisindən istifadə edərək problemi həll edirik
{TINA-nın Tərcüməçisi tərəfindən həll} |
TİNA müxtəlif formalarda verilən iki kompleks nömrəni necə asanlıqla idarə edir.
Tərcüməçi olmadan həll daha mürəkkəbdir. Fərqli vurma və bölgü üsullarını müqayisə edə bilmək üçün əvvəlcə qütb formasını təyin edəcəyik z1 və düzbucaqlı şəklindədir z2 .
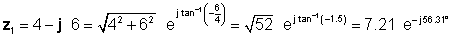
Sonra, ilk asan formaları istifadə edərək dörd həll tapırıq: əlavə və toplama işlənməsi üçün düzbucaqlı və vurma və bölmək üçün eksponent:
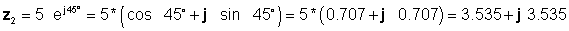
z 3 = z1 + z2 = 4 - j 6 + 3.535 + j 3.535 = 7.535 - j2.465
z 4 = z1 - z2 = 4 - j 6 - 3.535 - j 3.535 = 0.465 - j9.535
z 5 = z1 * z2 = 7.21 * 5 * ej(56.31 ° + 45 °) = 36.05 e -j11.31 ° = 36.03 * (cos (-11.31 °) +)j* günah (-11.31 °))
z 5 = 35.33 - j 7.07
z 6 = z1/z2= (7.21 / 5) * e j (56.31 ° -45 °) = 1.442 e - j 101.31 ° = 1.442 (cos (-101.31 °) +)j* günah (-101.31 °))
z 6 = -0.2828 - j 1.414
TINA Tərcüməçi ilə əldə edilən nəticələrlə razılaşır.
Çarpma düzbucaqlı formada həyata keçirilir:
z 5 =z1*z2 = (4-j6) * 3.535 * (1 +j) = 7.07 * (2-j3) * (1 +j) = 7.07 * (2-j3+j2 + 3) = 7.07 * (5-j) = 35.35-j7.07
Nəhayət bölmə düzbucaqlı formada həyata keçirilir:
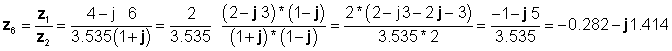
əvvəlki nəticələrlə razılaşdı.

