TINACloud-i çağırmaq üçün aşağıdakı nümunəvi sxemləri vurun və ya vurun və İnteraktiv DC rejimini Online onları təhlil etmək üçün seçin.
TINACloud-i çağırmaq üçün aşağıdakı nümunəvi sxemləri vurun və ya vurun və İnteraktiv DC rejimini Online onları təhlil etmək üçün seçin. TINACloud-a nümunələri düzəltmək və öz sxemlərinizi yaratmaq üçün aşağı qiymətə çıxın
Kirchhoff bərabərliklərinin tam dəstini asanlaşdırmağın başqa bir yolu mesh və ya döngə cərəyan metodudur. Bu metoddan istifadə edərək Kirchhoff-un cari qanunu avtomatik olaraq qane olur və yazdığımız döngə tənlikləri də Kirchhoffun gərginlik qanununu təmin edir. Kirchhoff-un mövcud qanunundan məmnun olmaq, dövrənin hər bir müstəqil döngəsinə mesh və ya döngə cərəyanları adlanan qapalı cərəyan döngələrini təyin etmək və bu cərəyanları dövrənin bütün digər miqdarlarını ifadə etmək üçün əldə edilir. Döngü cərəyanları bağlandığı üçün bir nodea axan cərəyan da düyündən axmalıdır; bu cərəyanlar ilə node tənliklərini yazmaq şəxsiyyətə səbəb olur.
Əvvəlcə mesh cərəyanları üsulunu nəzərdən keçirək.
Əvvəlcə qeyd edirik ki, mesh cərəyan metodu yalnız "planar" dövrələr üçün tətbiq olunur. Bir təyyarədə çəkildikdə planar sxemlərdə keçid telləri yoxdur. Çox vaxt, planar olmayan kimi görünən bir dövrə çəkərək, bunun əslində planar olduğunu müəyyənləşdirə bilərsiniz. Planar olmayan dövrələr üçün istifadə edin loop cari metod bu fəsildə daha sonra təsvir edilmişdir.
Mesh cərəyanları fikrini izah etmək üçün dövrə dallarını "balıq toru" kimi təsəvvür edin və şəbəkənin hər bir meshinə bir mesh cərəyanı təyin edin. (Bəzən deyilir ki, dövrənin hər “pəncərəsində” qapalı bir cərəyan döngəsi təyin olunur.)
  Şematik diaqram 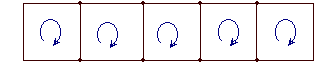  "Balıqçılıq şəbəkəsi" və ya dövrə grafiği |
Sxemi a adlı sadə bir rəsm ilə təmsil etmək texnikası graph, olduqca güclüdür. Bəri Kirchhoff qanunları komponentlərin təbiətindən asılı deyil, beton komponentləri laqeyd edə bilərsiniz və onları sadə xətt seqmentləri ilə əvəz edə bilərsiniz. filialları qrafikin Sxemləri qrafiklərlə təmsil etmək bizə riyazi texnikadan istifadə etməyə imkan verir grafik nəzəriyyəsi. Bu, bir dövrənin topoloji təbiətini araşdırmağa və müstəqil döngələri təyin etməyə kömək edir. Daha sonra bu mövzuya daha çox oxumaq üçün bu sayta qayıdın.
Mesh cari təhlili mərhələləri:
Hər mesh üçün bir mesh cərəyanı təyin edin. İstiqamət özbaşına olsa da, saat yönünün istiqamətini istifadə etmək adətdir.
Kirchhoffun gərginlik qanununu (KVL) hər mesh ətrafında, mesh cərəyanları ilə eyni istiqamətdə tətbiq edin. Bir rezistorun üzərindən iki və ya daha çox mesh cərəyanı varsa, rezistorun üzərindəki cərəyan mesh cərəyanlarının cəbri cəmi kimi hesablanır. Başqa sözlə, rezistordan axan bir cərəyan döngənin mesh cərəyanı ilə eyni istiqamətdə olarsa, müsbət işarəyə malikdir, əks halda cəmdə mənfi bir işarə var. Gərginlik mənbələri həmişəki kimi nəzərə alınır, İstiqamətləri mesh cərəyanı ilə eynidirsə, onların gərginliyi KVL tənliklərində müsbət, əks halda mənfi olur. Adətən, cari mənbələr üçün mənbədən yalnız bir mesh cərəyan axır və bu cərəyan mənbənin cərəyanı ilə eyni istiqamətdə olur. Bu belə deyilsə, daha sonra bu paraqrafda təsvir edilən daha ümumi döngə cari metodundan istifadə edin. Cari mənbələrə təyin edilmiş mesh cərəyanları olan döngələr üçün KVL tənliklərini yazmağa ehtiyac yoxdur.
Mesh axınları üçün yaranan döngü tənliklərini həll edin.
Mesh cərəyanlarını istifadə edərək dövrədə tələb olunan cərəyanı və ya gərginliyi təyin edin.
Təsəvvür et Aşağıdakı nümunə ilə metod:
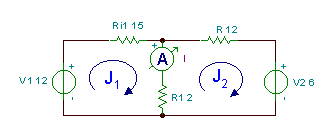
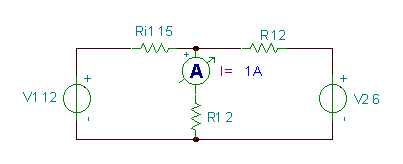
Aşağıdakı dövrədə cari I tapın.
Bu dövrədə iki meshes (və ya sol və sağ pəncərə) olduğunu görürük. Saat yönlü mesh cərəyanlarını J təyin edək1 və J2 meshlərə. Sonra Ohm qanunu ilə rezistorlar arasındakı voltajları ifadə edərək KVL tənliklərini yazırıq:
-V1 + J1* (R.i1+R1) - J2*R1 = 0
V2 - J1*R1 + J2* (R + R1) = 0
Sayısal olaraq:
-12 + J1* 17 - J2* 2 = 0
6 - J1* 2 + J2* 14 = 0
Ekspres J1 ilk tənlikdən: J1 = 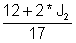

17-ə vur: 102 - 24 + 4 * J2 + 238 * J2 = 0 buna görə J2 = 
və J1 = 
Nəhayət, tələb olunan cari:
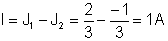
{Mesh cari metod}
Sys J1, J2
J1*(Ri1+R1)-J2*R1-V1=0
J1*R1+J2*(R1+R)+V2=0
son;
J1 = [666.6667m]
J2 = [- 333.3333m]
I: = J1-J2;
I = [1]
n kimi idxal numpy
#Mesh cari metodundan istifadə edin!
#Həll etmək istədiyimiz xətti tənliklər sistemimiz var
#I1,I2 üçün:
#I1*(Ri1+R1)+I2*Ri1-V1=0
#-V1+I1*Ri1+I2*(Ri1+R)+V2=0
#Əmsalların matrisini yazın:
A=n.array([[Ri1+R1,Ri1],[Ri1,Ri1+R]])
#Sabitlərin matrisini yazın:
b=n.massiv([V1,V1-V2])
x=n.linalg.həll edin(A,b)
I1=x[0]
I2=x[1]
çap("I1= %.3f"%I1)
çap("I2= %.3f"%I2)
I=I1
çap ("I= %.3f"%I)
Nəticələri TINA ilə yoxlayaq:

Sonrakı, əvvəlki nümunəni yenidən həll edək, amma daha ümumi ilə döngə cərəyanları metodu. Bu metodu istifadə edərək, qapalı olan cari loops, deyilir döngə cərəyanları, dövrənin boşluqlarına deyil, özbaşına təyin olunur müstəqil loops. Heç bir başqa döngədə olmayan hər döngədə ən azı bir komponent olmaqla, döngələrin müstəqil olmasını təmin edə bilərsiniz. Planar dövranlar üçün müstəqil döngələrin sayı görmək asan olan meshes sayına bərabərdir.
Müstəqil döngələrin sayını müəyyənləşdirməyin daha dəqiq bir yolu belədir.
İlə bir dövrə verilir b şöbələri və N qovşaqları. Müstəqil döngələrin sayı l edir:
l = b - N + 1
Bu, müstəqil Kirchhoff tənliklərinin sayının dövrədəki dallara bərabər olması lazım olduğundan və onsuz da yalnız olduğunu bilirik N-1 müstəqil node tənliklər. Buna görə Kirchhoffun bərabərliklərinin ümumi sayıdır
b = N-1 + l və buna görə l = b - N + 1
Bu tənlik, daha sonra bu saytda izah ediləcək qrafik nəzəriyyəsinin fundamental teoremindən irəli gəlir.
İndi əvvəlki nümunəni yenidən həll edək, amma daha sadə şəkildə, loop cari metodundan istifadə etməklə. Bu üsulla döngələrdə və ya başqa hər hansı bir döngədə istifadə etmək azaddır, amma J ilə loopu saxlayaq1 dövrənin sol meshində. Ancaq ikinci döngə üçün J ilə döngəni seçirik2, aşağıdakı şəkildə göstərildiyi kimi. Bu seçimin üstünlüyü J1 R1-dən keçən yeganə döngə cərəyanı olduğundan tələb olunan cərəyana bərabər olacaqdır. Bu, J2 hesablamağımıza ehtiyac olmadığını göstərir bütün. Qeyd edək ki, "həqiqi" cərəyandan fərqli olaraq, döngə cərəyanlarının fiziki mənası onları dövrə necə təyin etdiyimizdən asılıdır.

KVL tənlikləri:
J1 * (R1+Ri1) + J2 * R i1 - V1 = 0
-V1+ J1 * Ri1+ J2 * (R + Ri) + V2 = 0
və lazımi cari: I = J1
Numerically: J1*(15+2)+J2*15-12 = 0
-12 + J1 * 15 + J2 * (15 + 12) + 6 = 0
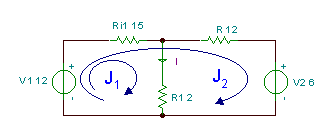
İkinci tənliyindən Express J2:
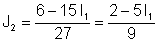
İlk bərabərliyi əvəz et:
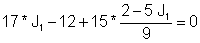
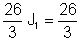
Beləliklə: J1 = I = 1 A
Əlavə nümunələr.
Məsələn 1
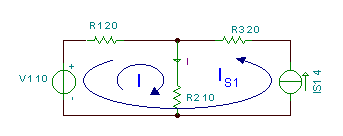
Aşağıdakı dövrədə cari I tapın.
Bu dövrədə döngə cərəyanları metodundan istifadə edirik. Dövrənin sol pəncərəsində tanımadığımız bir döngə cərəyanını götürürük I tələb olunan cərəyana bərabər olduğundan. Digər döngə cərəyanı Is1 qaynaq cərəyanına bərabərdir, buna görə də onu birbaşa olaraq qeyd edirik IS1.
Qeyd edək ki, bu döngə cərəyanının istiqaməti yox istiqamətini cari mənbə tərəfindən təyin olunduğundan saat istiqamətində. Bununla birlikdə, bu döngə cərəyanı artıq məlum olduğundan, döngə üçün KVL tənliyini yazmağa ehtiyac yoxdur IS1 alınır.
Buna görə həll ediləcək yeganə tənlik:
-V1 + I * R2 + R1 * (Mən - mənS1) = 0
buna görə
I = (V1 + R1 *IS1) / (R1 + R2)
Nümerik olaraq
I=(10+20*4)/(20+10)=3 A
TINA'nın simvolik analizini Analiz / Symbolic Analysis / DC Nəticə menyusundan çağıraraq bu nəticə əldə edə bilərsiniz:
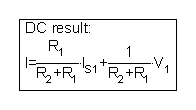
KVL tənliyini tərcüməçi tərəfindən həll edə bilərsiniz:
| {TINA-nın Tərcüməçisi tərəfindən həll} {Mesh cari metoddan istifadə edin} Sys I -V1 + I * R2 + R1 * (I - IS1) = 0 son; I = [3] |
Aşağıdakı nümunədə 3 cərəyan mənbəyi var və loop cərəyanları üsulu ilə həll etmək çox asandır.
Məsələn 2
Gərginlik V. tapın.
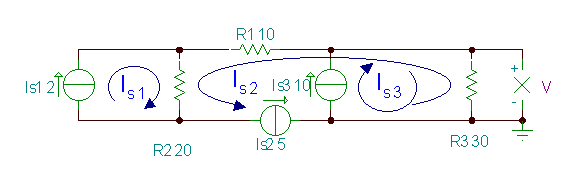

Bu nümunədə üç döngə cərəyanını seçə bilərik ki, hər biri yalnız bir cərəyan mənbəyindən keçir. Buna görə, üç döngə cərəyanının hamısı məlumdur və onlardan istifadə edərək yalnız bilinməyən gərginliyi, V-ni ifadə etməliyik.
R vasitəsilə cərəyanlar cəbri məbləği3:
V = (IS3 - MənS2) * R3= (10-5) * 30 = 150 V. Bunu TINA ilə təsdiqləyə bilərsiniz:.
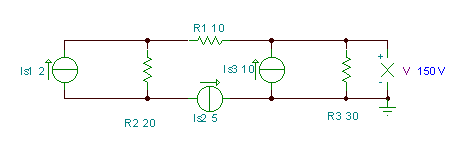

Sonra, həll etdiyimiz bir problemi yenidən həll edək Kirchhoff qanunları və Node potensial metodu fəsillər.
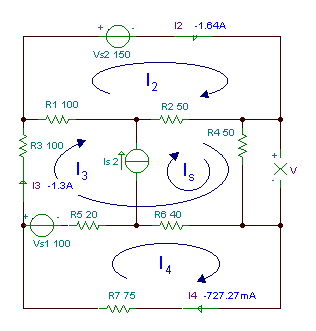
Məsələn 3
Rezistor R-nin gərginliyini V tapın4.
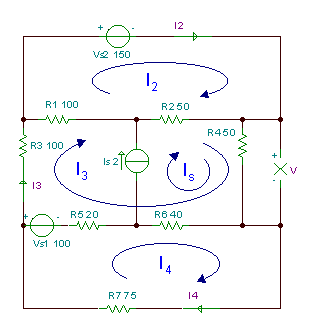

R1 = R3 = 100 ohm, R2 = R4 = 50 ohm, R5 = 20 ohm, R6 = 40 ohm, R7 = 75 ohm.
Bu problemi əvvəlki fəsillərdə həll etmək üçün ən azı 4 tənlik lazımdır.
Bu problemi döngə cərəyanları üsulu ilə həll etmək üçün dörd müstəqil döngə var, ancaq loop cərəyanlarının düzgün seçilməsi ilə, loop cərəyanlarından biri qaynaq cərəyanına bərabər olacaqdır.
Yuxarıdakı şəkildə göstərilən döngə cərəyanlarına əsasən, döngə tənlikləri:
VS1+I4* (R.5+R6+R7) - IS*R6 -İ3* (R.5 + R6) = 0
VS2 - Mən3* (R.1+R2) - IS*R2 + I2* (R.1 + R2) = 0
-VS1 + I3* (R.1 + R2 + R3 + R4 + R5 + R6) + IS* (R.2 +R4 + R6) - I4* (R.5 + R6) - Mən2* (R.1 + R2) = 0
Naməlum gərginlik V döngə cərəyanları ilə ifadə edilə bilər:
V = R4 * (I2 + I3)
Sayısal olaraq:
100 + I4* 135-2 * 40-I3* 60 = 0
150 + I2* 150-2 * 50-I3* 150 = 0
-100 + I3* 360 + 2 * 140-I4* 60-I2* 150 = 0
V = 50 * (2 + I)3)
Bu tənliklər sistemini həll etmək üçün Kramer qaydalarından istifadə edə bilərik:
I4 = D3/D
burada D sistemin determinantıdır. D4, mənim üçün determinant4, sistemin sağ tərəfi I sütunu üçün yerləşdirilərək meydana gəlir4əmsalları.
Sifariş formasında tənliklər sistemi:
- 60 * I3 + 135 * I4= -20
150 * I2-150 * I3 = - 50
-150 * I2+ 360 * I3 - 60 * I4= - 180
Beləliklə determinant D:
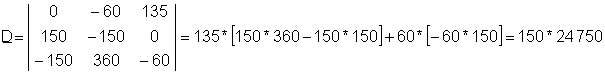
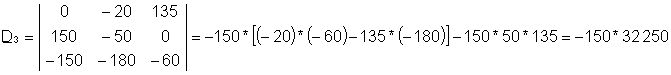
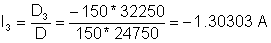
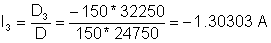
Bu tənlik sisteminin həlli aşağıdakılardır:
V = R4* (2 + I3) = 34.8485 V
TINA tərəfindən hesablanmış nəticə ilə cavabı təsdiqləyə bilərsiniz.
Sys I2, I3, I4
Vs2+I2*(R1+R2)-R2*Is-I3*(R1+R2)=0
-Vs1+I3*(R1+R2+R3+R4+R5+R6)+Is*(R2+R4+R6)-I2*(R1+R2)-I4*(R5+R6)=0
Vs1+I4*(R5+R6+R7)-Is*R6-I3*(R5+R6)=0
son;
I2 = [- 1.6364]
I3 = [- 1.303]
I4 = [- 727.2727m]
V: = R4 * (Is + I3);
V = [34.8485]
n kimi idxal numpy
#Həll etmək istədiyimiz xətti tənliklər sistemimiz var
#I1,I2,I3,I4 üçün:
#I1=Odur
#Vs2+I2*(R1+R2)-R2*I1-I3*(R1+R2)=0
#-Vs1+I3*(R1+R2+R3+R4+R5+R6)+I1*(R2+R4+R6)-I2*(R1+R2)-I4*(R5+R6)=0
#Vs1+I4*(R5+R6+R7)-I1*R6-I3*(R5+R6)=0
#Əmsalların matrisini yazın:
A=n.array([[1,0,0,0],[-R2,R1+R2,-(R1+R2),0],[R2+R4+R6,-(R1+R2),R1+R2+R3+R4+R5+R6,-(R5+R6)],[-R6,0,-(R5+R6),R5+R6+R7]])
#Sabitlərin matrisini yazın:
b=n.array([Is,-Vs2,Vs1,-Vs1])
x=n.linalg.həll edin(A,b)
I1,I2,I3,I4=x[0],x[1],x[2],x[3]
print(“I1= %.5f”%I1) #x[0]=I1
print(“I2= %.5f”%I2) #x[1]=I2
print(“I3= %.5f”%I3) #x[2]=I1
print(“I4= %.5f”%I4) #x[3]=I2
V=R4*(I1+I3)
çap(“V= %.5f”%V)
Bu nümunədə, hər bir bilinməyən döngə cərəyanı bir filial cərəyanıdır (I1, I3 və I4); buna görə nəticəni TINA-nın DC analiz nəticələri ilə müqayisə edərək yoxlamaq asandır.