TINACloud-i çağırmaq üçün aşağıdakı nümunəvi sxemləri vurun və ya vurun və İnteraktiv DC rejimini Online onları təhlil etmək üçün seçin.
TINACloud-i çağırmaq üçün aşağıdakı nümunəvi sxemləri vurun və ya vurun və İnteraktiv DC rejimini Online onları təhlil etmək üçün seçin. TINACloud-a nümunələri düzəltmək və öz sxemlərinizi yaratmaq üçün aşağı qiymətə çıxın
Sinusoidal bir gərginlik tənliklə təsvir edilə bilər:
v (t) = VM sin (ωt + Φ) və ya v (t) = VM cos (ωt + Φ)
| hara | v (t) | Gərginliyin ani dəyərləri, voltlarda (V). |
| VM | Gərginliyin maksimum və ya zirvəsindəki volt (V) | |
| T | Dövrü: Bir dövr üçün çəkilmiş vaxt, saniyədə | |
| f | Tezlik - 1 saniyədə, Hz (Hertz) və ya 1 / s-də dövrlərin sayı. f = 1 / T | |
| ω | Radians / s ilə ifadə olunan bucaq tezliyi ω = 2 * π * f və ya ω = 2 * π / T. | |
| Φ | Radianlar və ya dərəcələrlə verilən ilk mərhələ. Bu miqdar sinüs və ya kosinüs dalğasının = 0 dəyərini təyin edir. | |
| Qeyd: Bir sinusoidal gerilimin amplitudu bəzən V olaraq ifadə edilirEffeffektiv və ya RMS dəyəri. Bu V ilə bağlıdırM V əlaqəsinə görəM= √2VEff, və ya təxminən VEff = 0.707 VM |
Burada yuxarıda göstərilən şərtləri göstərmək üçün bir neçə nümunə var.
Avropada ev elektrik prizlərində 220 V AC geriliminin xüsusiyyətləri:
Effektiv dəyər: VEff = 220 V
Peak dəyəri: VM= √2 * 220 V = 311 V
Tezlik: f = 50 1 / s = 50 Hz
Açısal tezlik: ω = 2 * π * f = 314 1 / s = 314 rad / s
Dövrü: T = 1 / f = 20 ms
Vaxt funksiyası: v (t) = 311 sin (314 t)
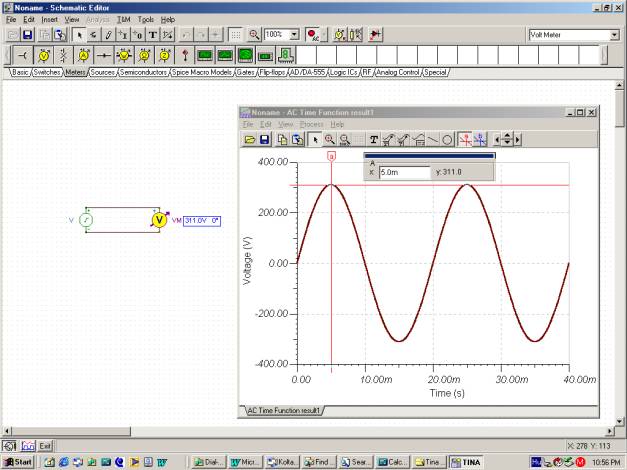
Tina'nın Analiz / AC Analizi / Saat Funksiyası komutunu istifadə edərək vaxt funksiyasını görürük.
Dövrün T = 20m və V olduğunu yoxlaya bilərsinizM = 311 V.
ABŞ-da ev elektrik prizində 120 V AC gərginliyin xüsusiyyətləri:
Effektiv dəyər: VEff = 120 V
Peak dəyəri: VM= √2 120 V = 169.68 V ≈ 170 V
Tezlik: f = 60 1 / s = 60 Hz
Açısal tezlik: ω = 2 * π * f = 376.8 rad / s ≈ 377 rad / s
Dövrü: T = 1 / f = 16.7 ms
Vaxt funksiyası: v (t) = 170 sin (377 t)
Qeyd edək ki, bu halda vaxt funksiyası ya v (t) = 311 sin (314 t + Φ) və ya v (t) = 311 cos (314 t + Φ) kimi verilə bilər. ilkin mərhələni bilmirsiniz.
İlkin faza eyni zamanda bir neçə gərginlik mövcud olduqda mühüm rol oynayır. Yaxşı praktik bir nümunə üç pilləli sistemdir ki, burada hər birinin digərlərinə nisbətən 120 ° faza keçidinə malik olan eyni pik dəyər, forma və tezlikin üç voltlu həddi mövcuddur. 60 Hz şəbəkəsində, vaxt funksiyaları aşağıdakılardır:
vA(t) = 170 sin (377 t)
vB(t) = 170 günah (377 t - 120 °)
vC(t) = 170 sin (377 t + 120 °)
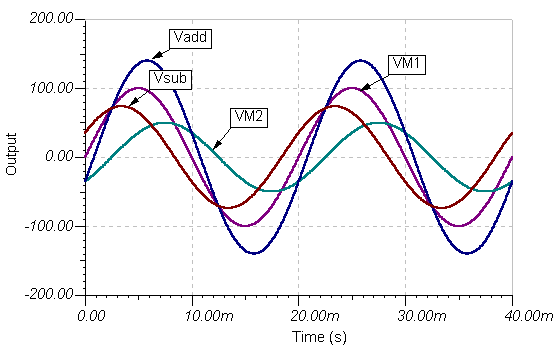
TINA ilə birlikdə aşağıdakı rəqəm TINA-nın geriləmə generatorları kimi bu vaxt funksiyaları ilə dövrəni göstərir.
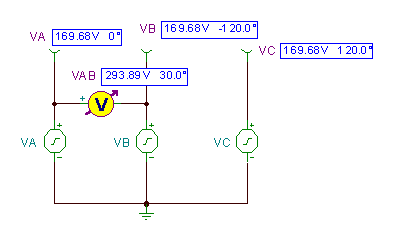

Gərginlik fərqi vAB= vA(t) - vB(t), Tina'nın Analiz / AC Analizi / Vaxt Funksiyası komutu tərəfindən həll edildi.
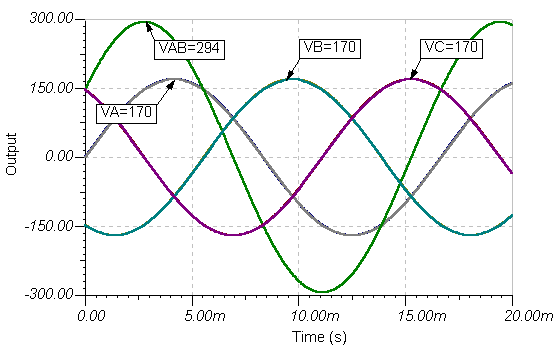

Qeyd edək ki, vAB (t) təxminən 294 V, 170 V zirvəsindən daha böyükdürA(t) və ya vB(t) gərginliklər deyil, sadəcə onların zirvələrinin həddən artıq olmamasıdır. Bu faz fərqinə bağlıdır. Nəticədə geriləmənin necə hesablanacağını müzakirə edəcəyik Ö3 * 170 @ 294 bu halda) sonra bu fəsildə və ayrıca ayrı-ayrılıqda Üç fazlı sistemlər fəsil.
Sinusoidal siqnalların xarakterik dəyərləri
Bir AC siqnalının dövründə daim dəyişkən olmasına baxmayaraq, bir dalğa digərini müqayisə etmək üçün bir neçə xarakterik dəyər müəyyən etmək asandır: bunlar zirvə, ortalama və kök-orta kvadrat (rms) dəyərlərdir.
Biz artıq zirvə dəyərinə sahibik VM , sadəcə, vaxt funksiyasının maksimum dəyəri, sinusoidal dalğanın amplitudasıdır.
Bəzən pik-to-pik (pp) dəyəri istifadə olunur. Sinusoidal gerilim və cərəyanlar üçün, zirvənin maksimum dəyəri zirvə dəyərinin iki qatına bərabərdir.
The orta dəyər sinüs dalğasının müsbət yarım dövrü üçün dəyərlərin aritmetik ortalamasıdır. Bu da adlanır mütləq orta çünki dalğa formasının mutlak dəyərinin ortalaması eynidır. Praktikada bu dalğa forması ilə qarşılaşırıq rektifikasiya bir dalğa ilə sinüs dalğası tam dalğa düzəldici adlanır.
Bir sinusoidal dalğanın mütləq ortalamasının göstərildiyi göstərilə bilər:
VAV= 2 / π VM ≅ 0.637 VM
Bir dövrün ortalamasının sıfır olduğunu unutmayın.
Bir sinusoidal gərginliyin və ya axınının rms və ya effektiv dəyəri eyni istilik enerjisini istehsal edən bərabər DC dəyərinə bərabərdir. Məsələn, 120 V-nin effektiv dəyərinə malik olan bir gərginlik, bir DC gərginlik qaynağından 120 V kimi bir ampuldə eyni istilik və işıq enerjisi istehsal edir. Sinusoidal dalğanın rms və ya effektiv dəyəri:

Vrms = VM / √2 ≅ 0.707 VM
Bu dəyərlər həm gərginlik, həm də cərəyanlar üçün eyni şəkildə hesablana bilər.
RMS dəyəri praktikada çox vacibdir. Aksi göstərilmədiyi təqdirdə, elektrik xəttinin AC gərginliyi (məsələn, 110V və ya 220V) rms dəyərlərində verilir. Çox AC metr sayğaclarda kalibr edilir və rms səviyyəsini göstərir.
Məsələn 1 220 V rms dəyəri olan bir elektrik şəbəkəsində sinusoidal gərginliyin pik dəyərini tapın.
VM = 220 / 0.707 = 311.17 V
Məsələn 2 110 V rms dəyəri olan bir elektrik şəbəkəsində sinusoidal gərginliyin pik dəyərini tapın.
VM = 110 / 0.707 = 155.58 V
Məsələn 3 RMS dəyəri 220 V isə sinusoidal gerilimin (mütləq) ortalamasını tapın.
Va = 0.637 * VM = 0.637 * 311.17 = 198.26 V
Məsələn 4 RMS dəyəri 110 V isə sinusoidal gerilimin mütləq ortalamasını tapın.
Örnek 2-dan olan gərginliyin zirvəsi 155.58 V və beləliklə:
Va = 0.637 * VM = 0.637 * 155.58 = 99.13 V
Məsələn 5 Mütləq orta arasındakı nisbəti tapın (V.a) və sinusoidal dalğa formasında rms (V) dəyərləri.
V / Va = 0.707 / 0.637 = 1.11
AC dövründə orta dəyərlər əlavə edə bilməyəcəyinizə diqqət yetirin, çünki düzgün olmayan nəticələrə gətirib çıxarır.
PHASORS
Əvvəlki hissədə gördüyümüz kimi, tez-tez AC dövrələrində sinusoidal gerilim və eyni tezliklərin cərəyanlarını əlavə etmək lazımdır. TİNA-dan istifadə edərək və ya trigonometrik münasibətləri istifadə edərək, siqnalları əlavə etmək mümkün olsa da, bu sözdə istifadə etmək daha rahatdır fasor üsul. Fasor sinusoidal siqnalın amplitüdünü və mərhələini təmsil edən kompleks bir nömrədir. Fasorun bütün fazaları üçün eyni olması lazım olan tezlikləri əks etdirmədiyini qeyd etmək vacibdir.
Fasor kompleks bir nömrə kimi işlənə bilər və ya kompleks düzlemdə planar bir ox kimi qrafik olaraq təmsil edilə bilər. Qrafik təmsilçiyə fasor diaqramı deyilir. Fasor diaqramlarından istifadə edərək, üçbucaq və ya paraleloqrafik qayda ilə mürəkkəb bir düzəldən fasorları əlavə edə və ya çıxara bilərsiniz.
Kompleks nömrələrin iki növü var: düzbucaqlı və qütb.
Düzbucaqlı görünüş şəklindədir + jb, harada j = Ö1 xəyali vahiddir.
Qütb təmsilçiliyi Ae şəklindədirj j Burada A mütləq dəyərdir (amplituda) və f pozitiv real oxdan, saat yönünün əks istiqamətində olan fasorun açısıdır.
Biz istifadə edəcəyik cəsarətli kompleks miqdarda məktublar.
İndi bir zaman funksiyasından müvafiq phasorun necə alınacağını görək.
Birincisi, dövrədə olan bütün gərginliklər kosin funksiyaları şəklində ifadə edilir. (Bütün gərginliklər bu formaya çevrilə bilər) fasor v (t) = V gərginliyinə bərabərdirM cos ( w t+f): VM = VMe jf , bu da kompleks pik dəyəri deyilir.
Məsələn, gərginliyi nəzərdən keçirin: v (t) = 10 cos ( w t + 30°)
Müvafiq phasor: 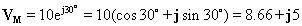
Vaxt funksiyasını bir fasordan eyni şəkildə hesablaya bilərik. İlk növbədə, fasoru polar formada yazırıq VM = VMe jr sonra müvafiq vaxt funksiyasıdır
v (t) = VM (cos (wt+r).
Məsələn, fasoru nəzərdən keçirin VM = 10 - j20 V
Qütb şəklində gətirmək:
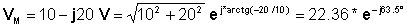
Və buna görə də vaxt funksiyası: v (t) = 22.36 cos (wt - 63.5°) V
Fasorlar tez-tez AC dövrlərində cərəyan və cərəyanların kompleks effektiv və ya rms dəyərini təyin etmək üçün istifadə olunur. V (t) = V verilmişdirMcos (wt+r) = 10cos (wt + 30°)
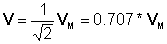
Sayısal olaraq:
v (t) = 10 * cos (wt-30°)
Kompleks effektiv (rms) dəyəri: V = 0.707 * 10 * e- j30° = 7.07 e- j30° = 6.13 - j 3.535
Əksinə: bir gərginliyin kompleks effektiv dəyəri:
V = - 10 + j 20 = 22.36 e j 116.5°
sonra kompleks pik dəyər: 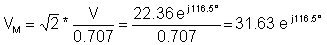
və vaxt funksiyası: v (t) = 31.63 cos ( wt + 116.5° ) V
Yuxarıda göstərilən üsulların qısa bir əsaslandırılması belədir. Bir vaxt funksiyası nəzərə alındı
VM (cos ( w t+r), təyin edək kompleks vaxt funksiyası kimi:
v (t) = VM e jr e jwt = VMe jwt = VM (cos (r) + j günahr)) e jwt
hara VM =VM e j r t = VM (cos (r) + j günahr)) yuxarıda göstərilən fasordur.
Məsələn, v (t) = 10 cos (wt + 30°)
v (t) = VMe jwt = 10 e j30 e jwt = 10e jwt (cos (30) +) j sin (30)) = e jwt (8.66 +j5)
Mürəkkəb vaxt funksiyasını tətbiq edərək, həm də gerçək bir hissə və xəyali bir hissə ilə bir təmsilimiz var. Nəticəmizin əsl hissəsini alaraq həmişə orijinal real funksiyasını bərpa edə bilərik: v (t) = Re {v(t)}
Lakin kompleks vaxt funksiyası böyük üstünlüyə malikdir, çünki nəzərə alınmıĢ AC dövrələrində bütün kompleks vaxt eynidırjwt çarpan, biz bu faktoru amil və yalnız phasors ilə işləyə bilər. Bundan başqa, praktikada biz e istifadə etmirikjwt ümumiyyətlə - zaman funksiyalarından fazorlara və arxaya çevrilmələr.
Fasorların istifadə edilməsinin üstünlüyünü göstərmək üçün aşağıdakı nümunəyə baxaq.
Məsələn 6 Gerilimlərin məbləğini və fərqini tapın:
v1 = 100 cos (314 * t) və v2 = 50 cos (314 * t-45°)
Əvvəlcə hər iki voltajın fazasını yazın:
V1M = 100 V2M= 50 e - j 45° = 35.53 - j 35.35
Beləliklə:
Vəlavə etmək = V1M + V2M = 135.35 - j 35.35 = 139.89 e- j 14.63°
Valt = V1M - V2M = 64.65 + j35.35 = 73.68 və j 28.67°
və sonra zaman funksiyaları:
vəlavə etmək(t) = 139.89 * cos (wt - 14.63°)
valt(t) = 73.68 * cos (wt + 28.67°)
Bu sadə nümunə göstərir ki, phasors.is metodu AC problemlərinin həlli üçün son dərəcə güclü bir vasitədir.
Tina'nın tərcüməçisindəki vasitələrdən istifadə edərək problemi həll edək.
{v1 + v2 hesablanması}
v1: = 100
v2: = 50 * exp (-pi / 4 * j)
v2 = [35.3553-35.3553 * j]
v1add: = v1 + v2
v1add = [135.3553-35.3553 * j]
abs (v1add) = [139.8966]
radtodeg (arc (v1add)) = [- 14.6388]
{v1-v2 hesablanması}
v1sub: = v1-v2
v1sub = [64.6447 + 35.3553 * j]
abs (v1sub) = [73.6813]
radtodeg (arc (v1sub)) = [28.6751]
#v1+v2 hesablanması
m kimi riyaziyyatı idxal edin
c kimi idxal cmath
v1=100
v2=50*c.exp(kompleks(0,-c.pi/4))
çap ("v2 =", v2)
vadd=v1+v2
çap ("vadd =", vadd)
çap ("abs(vadd)=",abs(vadd))
çap(“dərəcə(qövs(vadd))=”,m.dərəcə(c.faza(vadd)))
#v1-v2 hesablanması
vsub=v1-v2
çap ("vsub =", vsub)
çap ("abs(vsub)=",abs(vsub))
çap("dərəcə(qövs(vsub))=",m.derece(c.faza(vsub)))
Genlik və faza nəticələri əl hesablamalarını təsdiqləyir.
İndi TINA'nın AC analizini istifadə edərək nəticəni yoxlamağa imkan verir.
Təhlili yerinə yetirmədən əvvəl, əmin olun AC üçün əsas funksiya ia qurdular kosin ci Redaktor Seçimləri Görüş / Seçim menyusundan informasiya qutusu. Bu parametrenin rolunu açıqlayacağıq Məsələn 8.
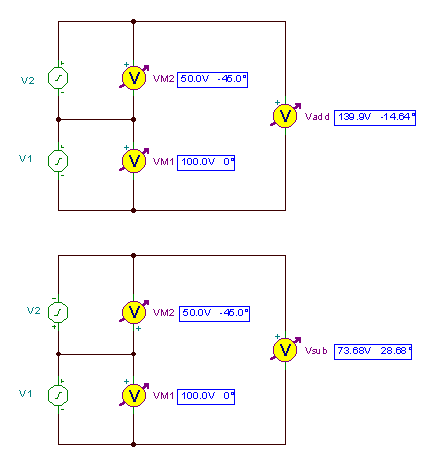
Sxemlər və nəticələr:
Yenə də nəticə eyni. Vaxt funksiyası qrafikləri aşağıdakılardır:
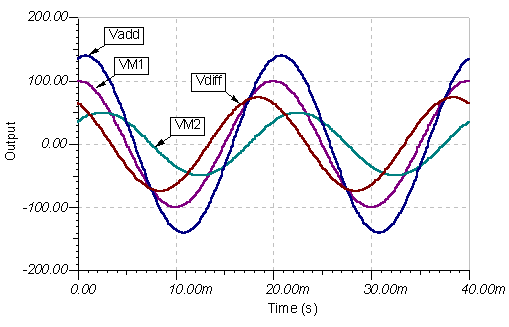
Məsələn 7 Gerilimlərin məbləğini və fərqini tapın:
v1 = 100 sin (314 * t) və v2 = 50 cos (314 * t-45°)
Bu nümunə yeni bir sual yaradır. İndiyə qədər bütün vaxt funksiyalarının kosin funksiyaları olaraq verilməsini tələb etdik. Sinüs kimi verilən bir vaxt funksiyası ilə nə edəcəyik? Çözüm sinüs funksiyasını kosinüs funksiyasına çevirməkdir. Trigonometrik əlaqə sin (x) = cos (x-p/ 2) = cos (x-90°), nümunə aşağıdakı kimi redaktə edilə bilər:
v1 = 100 cos (314t - 90)°) və v2 = 50 cos (314 * t - 45°)
İndi voltajların fazaları aşağıdakılardır:
V1M = 100 e - j 90° = -100 j V2M= 50 e - j 45° = 35.53 - j 35.35
Beləliklə:
V əlavə etmək = V1M + V2M = 35.53 - j 135.35
V alt = V1M - V2M = - 35.53 - j 64.47
və sonra zaman funksiyaları:
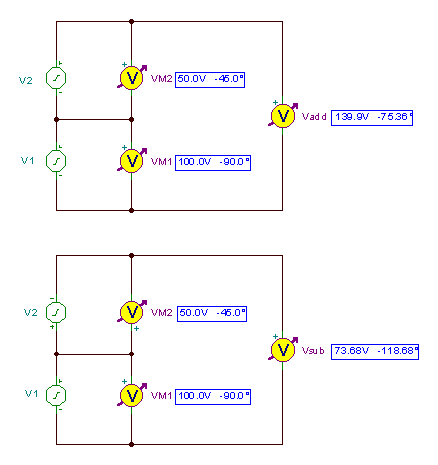
vəlavə etmək(t) = 139.8966 cos (wt-75.36°)
valt(t) = 73.68 cos (wt-118.68°)
Tina'nın tərcüməçisindəki vasitələrdən istifadə edərək problemi həll edək.
{v1 + v2 hesablanması}
v1: = - 100 * j
v2: = 50 * exp (-pi / 4 * j)
v2 = [35.3553 - 35.3553 * j]
v1add: = v1 + v2
v1add = [35.3553-135.3553 * j]
abs (v1add) = [139.8966]
radtodeg (arc (v1add)) = [- 75.3612]
{v1-v2 hesablanması}
v1sub: = v1-v2
v1sub = [- 35.3553 - 64.6447 * j]
abs (v1sub) = [73.6813]
radtodeg (arc (v1sub)) = [- 118.6751]
#v1+v2 hesablanması
m kimi riyaziyyatı idxal edin
c kimi idxal cmath
v1=100
v2=50*c.exp(kompleks(0,-c.pi/4))
çap ("v2 =", v2)
vadd=v1+v2
çap ("vadd =", vadd)
çap ("abs(vadd)=",abs(vadd))
çap(“dərəcə(qövs(vadd))=”,m.dərəcə(c.faza(vadd)))
#v1-v2 hesablanması
vsub=v1-v2
çap ("vsub =", vsub)
çap ("abs(vsub)=",abs(vsub))
çap("dərəcə(qövs(vsub))=",m.derece(c.faza(vsub)))
Tinanın AC Analizi ilə nəticəni yoxlayaq
Məsələn 8
Gerilimlərin məbləğini və fərqini tapın:v1 = 100 günah (314 * t) və v2 = 50 sin (314 * t-45°)
Bu nümunə daha bir məsələni qaldırır. Bütün gərginlik sinüs dalğaları kimi verilirsə və nəticəni sinüs dalğası kimi görmək istəyirik ?. Əlbəttə ki, hər iki gərginliyi kosinus funksiyalarına çevirə bilərik, cavabı hesablaya bilərik və nəticəni yenidən sinus funksiyasına çevirə bilərik - ancaq bu lazım deyil. Sinus dalğalarından kosinus dalğalarındakı kimi fazalar yarada, sonra da amplitüdlərini və fazlarını nəticədə sinus dalğalarının amplitüdü və fazası olaraq istifadə edə bilərik.
Sinüs dalğalarının kosinüs dalğalarına çevrilməsi ilə eyni nəticə verəcəkdir. Əvvəlki nümunədə görə bildiyimiz kimi, bu,j və sonra cos (x) = sin (x-90°) bir sine dalğasına çevirməklə əlaqəsi. Bu, çarpma ilə bərabərdir j. Başqa sözlə,j × j = 1, funksiyanı təmsil etmək üçün sinus dalğalarının amplitüd və mərhələlərini birbaşa əldə edən və daha sonra birbaşa onlara dönə biləcək fazaları istifadə edə bilərik. Həmçinin, mürəkkəb vaxt funksiyaları haqqında eyni şəkildə düşünməklə, sine dalğalarını kompleks vaxt funksiyalarının xəyali hissəsi kimi nəzərdən keçirə və tam kompleks vaxt funksiyasını yaratmaq üçün kosinüs funksiyasına əlavə edə bilərik.
Sinaz funksiyalarını fazaların əsası kimi istifadə edərək bu misalın həllini görək (transformasiya edən günah ( w t) real vahid fasoruna (1)).
V1M = 100 V2M= 50 e - j 45° = 35.53 - j 35.35
Beləliklə:
V əlavə etmək = V1M + V2M = 135.53 - j 35.35
V alt = V1M - V2M = 64.47+ j 35.35
Phasors, nümunə 6-da olduğu kimi eynidır, lakin vaxt funksiyaları deyil:
v3(t) = 139.9sin (wt - 14.64°)
v4(t) = 73.68sin (wt + 28.68°)
Gördüyünüz kimi, sinus funksiyalarından istifadə edərək nəticəni əldə etmək çox asandır, xüsusən də ilk məlumatlarımız sinus dalğaları olduqda. Bir çox dərslik sinus dalğasından fazorların əsas funksiyası kimi istifadə etməyi üstün tutur. Praktikada hər iki üsuldan da istifadə edə bilərsiniz, ancaq onları qarışdırmayın.
Phasorları yaratdığınızda, bütün vaxt funksiyalarının əvvəl sinüs və ya kosinüsünə çevrildiyi çox vacibdir. Sinüs funksiyalarından başlasanız, həllər phasors'dan zaman funksiyalarına dönərkən sinüs funksiyaları ilə təmsil olunmalıdır. Kosinüs funksiyaları ilə başlasanız eyni olur.
Tina-nın interaktiv rejimi ilə eyni problemi həll edək. Sinüs funksiyalarını phasorları yaratmaq üçün əsas kimi istifadə etməkdən ötrü əmin olun AC üçün əsas funksiya müəyyən edilir sine ci Redaktor Seçimləri Görünüş / Seçim menyusundan informasiya qutusu.
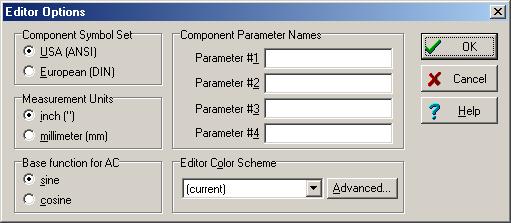

Dalğa formalarının məbləği və fərqi və nəticəsi üçün sxemlər:
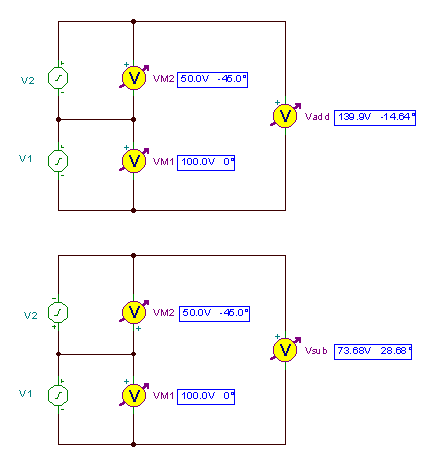
və vaxt funksiyaları: