TINACloud-i çağırmaq üçün aşağıdakı nümunəvi sxemləri vurun və ya vurun və İnteraktiv DC rejimini Online onları təhlil etmək üçün seçin.
TINACloud-a nümunələri düzəltmək və öz sxemlərinizi yaratmaq üçün aşağı qiymətə çıxın

Sinusoidal mənbələri olan AC dövrələri üçün Thévenin Teoremi, DC dövrələri üçün öyrəndiklərimizə çox oxşayır. Yeganə fərq, düşünməyimizdir empedans yerinə Müqavimət. Qısaca deyildiyi kimi, Thevenin AC dövrələri üçün teoremi belə deyir:

İstənilən iki terminal xətti dövrə, bir gərginlik mənbəyindən (V) ibarət ekvivalent dövrə ilə əvəz edilə bilər_Th) və bir sıra empedans (Z._Th).

Başqa sözlə, Thévenin Teoremi, mürəkkəb bir dövrəni yalnız bir gərginlik mənbəyi və bir sıra bağlı empedans ehtiva edən sadə bir ekvivalent dövrə ilə əvəz etməyə imkan verir. Teorem həm nəzəri, həm də praktik baxımdan çox vacibdir.

Thvenin ekvivalent dövrəsinin yalnız terminallarda ekvivalentliyi təmin etdiyini qeyd etmək vacibdir. Aydındır ki, orijinal dövrənin daxili quruluşu və Thévenin ekvivalenti tamamilə fərqli ola bilər. Empedansın tezlikdən asılı olduğu AC dövrələri üçün bərabərlik etibarlıdır bir yalnız tezlik.

Thévenin Teoremindən istifadə etmək xüsusilə faydalıdır:

· bir dövrənin müəyyən bir hissəsini cəmləşdirmək istəyirik. Sxemin qalan hissəsi sadə bir Thévenin ekvivalenti ilə əvəz edilə bilər.

· terminallarda fərqli yük dəyərləri olan dövrəni öyrənməliyik. Thévenin ekvivalentindən istifadə edərək hər dəfə mürəkkəb orijinal dövrə təhlil etməkdən çəkinə bilərik.

Thvenin ekvivalent dövrəsini iki addımla hesablaya bilərik:

1. Hesablayın Z_Th. Bütün mənbələri sıfıra qoyun (gərginlik mənbələrini qısa dövrə və cərəyan mənbələrini açıq dövrə ilə dəyişdirin) və sonra iki terminal arasındakı ümumi empedansı tapın.

2. Hesablayın V_Th. Terminallar arasında açıq cərəyan gərginliyini tapın.

Artıq DC dövrələri üçün təqdim olunan Norton Teoremi, AC dövrələrində də istifadə edilə bilər. AC dövrələrinə tətbiq olunan Norton Teoremi, şəbəkənin a ilə əvəz edilə biləcəyini bildirir cari mənbə ilə paralel olaraq empedans.

Norton ekvivalent dövrəsini iki addımda hesablaya bilərik:

1. Hesablayın Z_Th. Bütün mənbələri sıfıra qoyun (gərginlik mənbələrini qısa dövrə və cərəyan mənbələrini açıq dövrə ilə dəyişdirin) və sonra iki terminal arasındakı ümumi empedansı tapın.

2. Hesablayın I_Th. Terminallar arasındakı qısa dövrə cərəyanını tapın.

İndi bəzi sadə nümunələrə baxaq.

Məsələn 1

Tezlikdə A və B nöqtələri üçün şəbəkənin Thivevenin ekvivalentini tapın: f = 1 kHz, v_S(T) = 10 cosw ×t V.

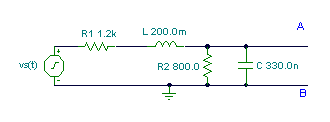
İlk addım A və B nöqtələri arasındakı açıq dövrə gərginliyini tapmaqdır:

İstifadə edərək açıq dövrə gərginliyi gərginlik bölməsi:

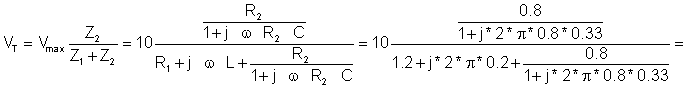
= -0.065 - j2.462 = 2.463 e^-J91.5º V

TINA ilə yoxlanılır:

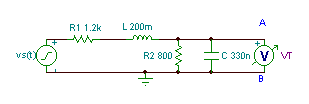
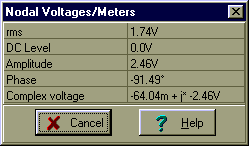
İkinci addım, gərginlik mənbəyini qısa bir dövrə ilə əvəz etmək və A və B nöqtələri arasındakı maneəni tapmaq:

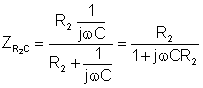
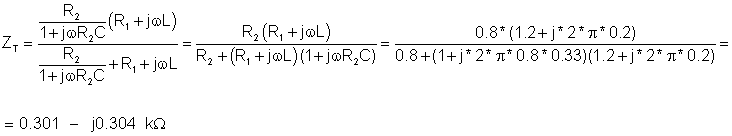
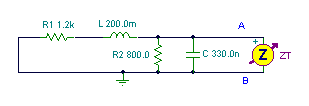
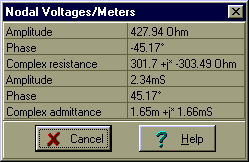
Budur Thévenin ekvivalenti dövrü, yalnız 1kHz tezlikdə etibarlıdır. Bununla birlikdə əvvəlcə CT-nin kapasitansını həll etməliyik. Münasibətlərdən istifadə 1 /wC_T = 304 ohm, biz C tapa bilərsiniz_T = 0.524 uF

İndi həllimiz var: R_T = 301 ohm və C_T = 0.524 m F:

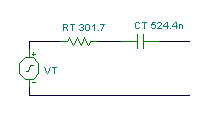
Daha sonra, Thévenin ekvivalent dövrə hesablamalarımızı yoxlamaq üçün TINA-nın tərcüməçisini istifadə edə bilərik:

Qeyd edək ki, yuxarıdakı siyahıda “replus” funksiyasından istifadə etdik. Replus iki empedansın paralel ekvivalenti üçün həll edir; yəni məhsulu iki paralel empedansın cəmi üzərində tapır.

Məsələn 2

Dövrün Norton ekvivalentini tapın Misal 1-də.

f = 1 kHz, v_S(T) = 10 cosw ×t V.

Ekvivalent empedans eynidır:

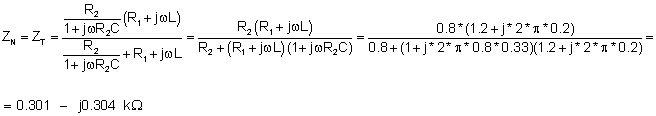
Z_N= (0.301-j0.304) kW

Sonra, qısa qapanma cərəyanını tapın:

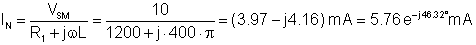
I_N = (3.97-j4.16) mA

Əl hesablamalarımızı TINA-nın nəticələrinə görə yoxlaya bilərik. Əvvəlcə açıq dövrə empedansı:

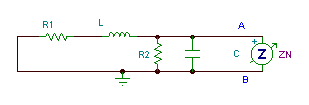
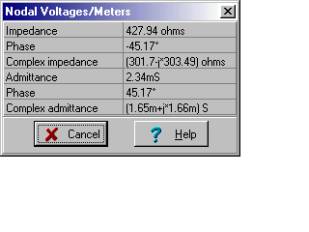
Sonra qısa qapanma cərəyanı:

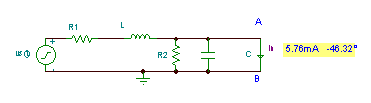
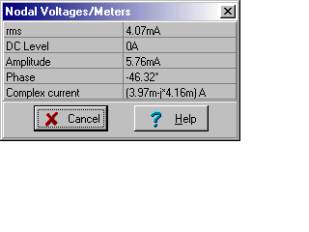
Və nəhayət Norton ekvivalenti:

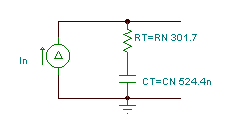
Sonra Norton ekvivalent dövrə komponentlərini tapmaq üçün TINA-nın tərcüməçisini istifadə edə bilərik:

Məsələn 3

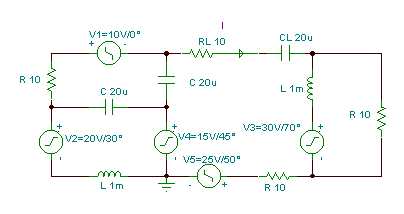
Bu dövrədə yük seriyaya bağlı olan RL və CL-dir. Bu yük komponentləri axtardığımız dövrənin bir hissəsi deyildir. Dövrün Norton ekvivalentindən istifadə edərək yükdəki cərəyanı tapın.

v₁(t) = 10 cos wt V; v₂(t) = 20 cos (wt + 30°) V; v₃(t) = 30 cos (wt + 70°) V;

v₄(t) = 15 cos (wt + 45°) V; v₅(t) = 25 cos (wt + 50°) V; f = 1 kHz.

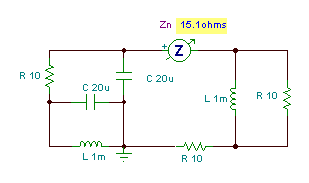
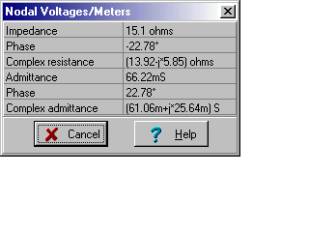
Əvvəlcə açıq dövrə ekvivalent impedans Z tapın_eq əllə (yük olmadan).

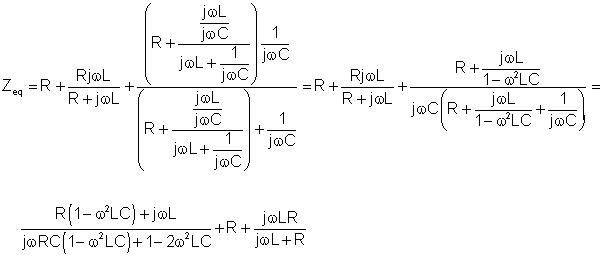
Nümerik olaraq

Z_N = Z_eq = (13.93 - j5.85) ohm.

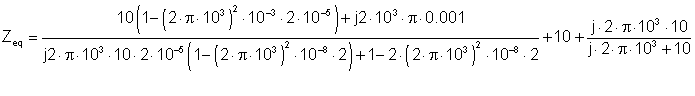
Aşağıda TINA-nın həllini görürük. Qeyd edək ki, sayğacdan istifadə etməzdən əvvəl bütün gərginlik mənbələrini qısa dövrələrlə əvəzlədik.

İndi qısamüddətli cərəyan:

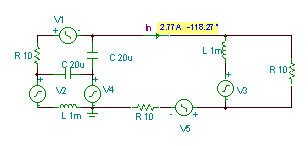
Qısa qapanma cərəyanının hesablanması olduqca mürəkkəbdir. İpucu: bu Superpozisiya istifadə etmək üçün yaxşı bir vaxt olar. Bir yanaşma, alınan hər bir gərginlik mənbəyi üçün yük cərəyanını (düzbucaqlı formada) tapmaq olardı. Sonra cəmi əldə etmək üçün beş qismən nəticə çıxarın.

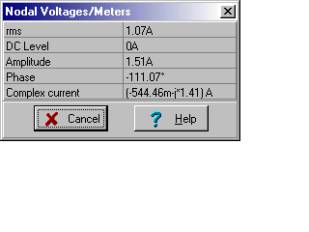
TINA-nın verdiyi dəyərdən yalnız istifadə edəcəyik:

i_N(t) = 2.77 cos (w ×t-118.27°) A

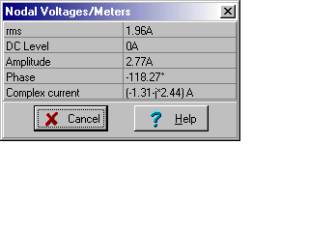
Hamısını bir yerə qoyaraq (şəbəkəni Norton ekvivalenti ilə əvəz etmək, yük komponentlərini çıxışa yenidən yükləmək və yükə bir ammetr qoymaq), axtardığımız yük cərəyanının həllini tapdıq:

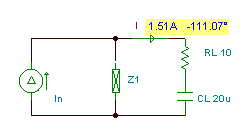
Əl hesablaması ilə cari bölgüdən istifadə edərək yük cərəyanını tapa bildik:

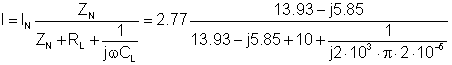
Nəhayət

I = (- 0.544 - j 1.41) A

və vaxt funksiyası