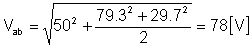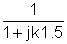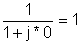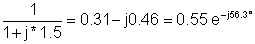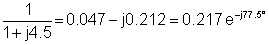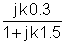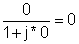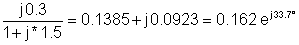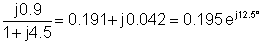Klik eller tryk på Eksempel kretserne nedenfor for at påkalde TINACloud og vælg den interaktive DC-tilstand for at analysere dem online.
Få en billig adgang til TINACloud for at redigere eksemplerne eller oprette dine egne kredsløb

Fourier sætning angiver, at enhver periodisk bølgeform kan syntetiseres ved at tilføje passende vægtede sinus- og cosinus-termer for forskellige frekvenser. Sætningen er godt dækket i andre lærebøger, så vi sammenfatter kun resultaterne og viser nogle eksempler.

Lad vores periodiske funktion være f (t) = f (t ±nT) hvor T er tiden for en periode og n er et heltal.

w₀= 2p/ T den grundlæggende vinkelfrekvens.

Ved Fourier sætning, den periodiske funktion kan skrives som følgende sum:

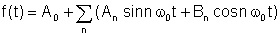
hvor

A_n og B_n er de Fourier-koefficienter og summen er den Fourier-serien.

En anden form, sandsynligvis lidt mere praktisk:

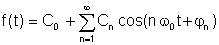
hvor

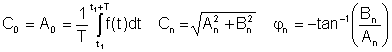
A₀ = C₀ er DC- eller gennemsnitsværdien, A₁, B.₁ og C₁ er de grundlæggende komponenter, og de andre er de harmoniske udtryk.

Selvom det kun kræves nogle få udtryk for at tilnærme nogle bølgeformer, vil andre kræve mange udtryk.

Generelt, jo flere inkluderede termer, jo bedre er tilnærmelsen, men for bølgeformer, der indeholder trin, såsom rektangulære impulser, Gibbs fænomen kommer i spil. Efterhånden som antallet af termer stiger, bliver overskuddet koncentreret i en stadig mindre periode.

An selv funktion f (t) = f (-t) (aksesymmetri) kræver kun kosinus-termer.

An ulige funktion f (t) = - f (-t) (punktsymmetri) kræver kun sine termer.

En bølgeform med spejl eller halvbølge symmetri har kun ulige harmoniske i sin Fourier-repræsentation.

Her vil vi ikke beskæftige os med udvidelsen af ​​Fourier-serien, men vil kun bruge en given sum af sines og cosinus som en excitation for et kredsløb.

I de tidligere kapitler i denne bog behandlede vi sinusformet ophidselse. Hvis kredsløbet er lineært, vil superposition sætning er gyldig. For et netværk med nonsinusoidal periodisk excitation tillader superposition os det beregne strømme og spændinger på grund af hver Fourier sinusform en ad gangen. Når alle er beregnet, opsummerer vi endelig responsens harmoniske komponenter.

Det er lidt kompliceret at bestemme de forskellige udtryk for de periodiske spændinger og strømme, og det kan faktisk give en overbelastning af information. I praksis vil vi gerne blot foretage målinger. Vi kan måle de forskellige harmoniske udtryk vha harmonisk analysator, spektrumanalysator, bølgeanalysator eller Fourier-analysator. Alle disse er kompliceret og giver sandsynligvis flere data end nødvendigt. Nogle gange er det tilstrækkeligt at beskrive et periodisk signal kun med dets gennemsnitlige værdier. Men der er flere slags gennemsnitlige målinger.

GENNEMSNIT VÆRDIER

Simpelt gennemsnit or DC udtryk blev set i Fourier-repræsentationen som A₀

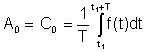
Dette gennemsnit kan måles med instrumenter som Deprez DC instrumenter.

Effektiv værdi or rms (rod middelværdi) har følgende definition:

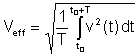
Dette er den vigtigste gennemsnitsværdi, fordi varmen, der spredes i modstande, er proportional med den effektive værdi. Mange digitale og nogle analoge voltmetre kan måle den effektive værdi af spændinger og strømme.

Absolut gennemsnit

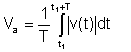
Dette gennemsnit er ikke længere vigtigt; tidligere instrumenter målte denne form for gennemsnit.

Hvis vi kender Fourier-repræsentationen af ​​en spænding eller strømbølgeform, kan vi også beregne gennemsnitsværdierne som følger:

Simpelt gennemsnit or DC udtryk blev set i Fourier-repræsentationen som A₀ = C₀

Effektiv værdi or rms (rod middelværdi) er efter integration af Fourier-serien af ​​spændingen:

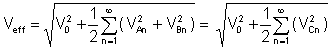
klirr faktor er et meget vigtigt forhold mellem gennemsnitsværdierne:

Det er forholdet mellem den effektive værdi af de højere harmoniske udtryk til den effektive værdi af den grundlæggende harmoniske:

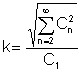
Der ser ud til at være en modsigelse her - vi løser netværk med hensyn til harmoniske komponenter, men vi måler gennemsnitlige størrelser.

Lad os illustrere metoden ved enkle eksempler:

Eksempel 1

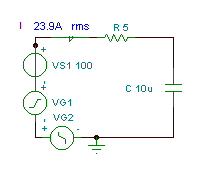
Find tidsfunktionen og den effektive (rms) værdi for spændingen v_C(T)

Prøv at bruge superpositionsteoremet til at løse problemet.

Det første trin er at finde overførselsfunktionen som en funktion af frekvensen. For at gøre det lettere, skal du bruge substitutionen: s = j w

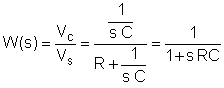
Udskift nu komponentværdierne og s = jk w₀hvor k = 0; 1; 3 i dette eksempel og w₀= 30 krad / s. I V, A, ohm, mF og Mrad / s enheder:

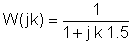
Det er nyttigt at bruge en tabel til at organisere trinnene i den numeriske løsning:

Vi kan sammenfatte trinene i superposition-løsningen i en anden tabel. Som vi allerede har set, bør vi for at finde en komponents komplekse spidsværdi multiplicere den komplekse spidsværdi af komponenten i excitationen med værdien af ​​den komplekse overførselsfunktion:

Og endelig kan vi give tidsfunktionen ved at kende de komplekse spidsværdier for komponenterne:

v_C(t) = 100 + 110 cos (w₀t - 56.3°) + 6.51 cos (3w₀t - 167.5°) V

Spændingens rms (effektive) værdi er:

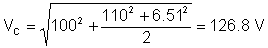
Som du kan se, måler TINA's måleinstrument denne rms-værdi.

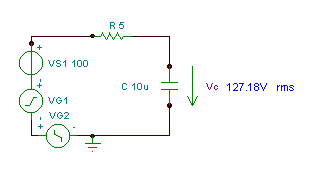
Eksempel 2

Find tidsfunktionen og den effektive (rms) værdi for den aktuelle i (t)

Prøv at løse problemet ved hjælp af superpositionsteoremet.

Udskift nu de numeriske værdier og s = jk w_0,hvor k = 0; 1; 3 i dette eksempel.

I V, A, ohm, mF og Mrad / s enheder:

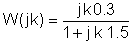
Det er nyttigt at bruge en tabel under den numeriske løsning:

Vi kan sammenfatte trinene i superpositionen i en anden tabel. Som vi allerede har set, bør vi for at finde en komponents topværdi multiplicere den komplekse spidsværdi af den komponent af excitationen med værdien af ​​den komplekse overførselsfunktion. Brug de komplekse spidsværdier for komponenterne i excitationen:

Og til sidst, når vi kender de komplekse spidsværdier for komponenterne, kan vi angive tidsfunktionen:

I (t) = 32.4 cos (w₀t + 33.7°) + 5.85 cos (3w₀t - 77.5°) [EN]

Than rms værdien af ​​strømmen:

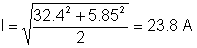
Du kan ofte foretage en sundhedsundersøgelse for en del af løsningen. For eksempel kan en kondensator have en jævnspænding, men ikke en jævnstrøm.

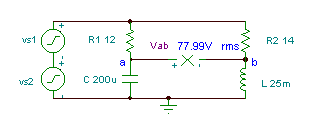
Eksempel 3

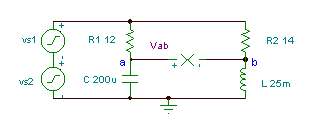
Få tidsfunktionen for spændingen V_ab if R₁= 12 ohm, R₂ = 14 ohm, L = 25 mH og

Det første trin er at finde overførselsfunktionen:

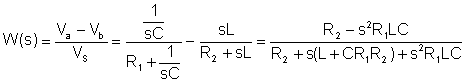
Udskiftning af numeriske værdier i V-, A-, ohm-, mH-, mF-, kHz-enheder:

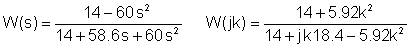
Sammenlægning af de to tabeller:

k V Sk		V ABK
0 50		50
1 80		79.3 og-j66.3
2 30 ej60		29.7 og-j44.7

v_ab(t) = 50 + 79.3 cos (w₁t - 66.3°) + 29.7 cos (2w₁t - 44.7°) [V]

og rms-værdien: