 Kliknite ali se dotaknite spodnjih vzorčnih vezij, da pokličete TINACloud in izberite način Interactive DC za analizo na spletu.
Kliknite ali se dotaknite spodnjih vzorčnih vezij, da pokličete TINACloud in izberite način Interactive DC za analizo na spletu. Pridobite poceni dostop do TINACloud, da uredite primere ali ustvarite lastna vezja
V tem in naslednjih poglavjih bomo predstavili zelo pomembno temo: AC ali izmenični tok. Naziv izmenični tok ni zelo natančen in običajno pokriva kroge z sinusno napetostjo in tokovi; izmenični tok lahko pomeni tudi poljubno trenutno valovno obliko. Pomen AC napetosti je, da se ta vrsta napetosti uporablja za glavni vir električne energije v domovih in industriji po vsem svetu. Prav tako je osnova za številne elektronike, telekomunikacije in industrijske aplikacije.
Za ravnanje s sinusoidnimi valovnimi oblikami in z njimi povezanimi vezji bomo uporabili preprosto in elegantno metodo, imenovano metoda fazorjev. Fazorji temeljijo na lastnostih kompleksnih števil, ki so idealne za predstavljanje sinusnih veličin. V tem poglavju bomo povzeli glavna dejstva o kompleksnih številkah in njihovem delovanju. Pokazali bomo tudi, kako TINA-ov Interpreter olajša izračune s kompleksnimi številkami.
Kompleksna števila so sestavljena iz dveh delov: a pravi del (x), ki je resnično število, in tako imenovano imaginarni del (y), ki je realno število, pomnoženo z 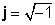
z = x + jy
Kje 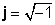
Primeri kompleksnih števil:
z 1 = 1 + j
z 2 = 4-2 j
z 3 = 3- 5j
Kompleksne številke so bile prvotno uvedene v sedemnajstem stoletju, da bi predstavljale korenine polinomov, ki jih ni bilo mogoče predstavljati samo z dejanskimi številkami. Na primer, korenine enačbe x2 + 2x + 2 = 0 lahko opišemo le kot 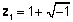
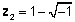
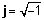
Geometrična predstavitev kompleksnih števil
Pravokotna oblika
Ker je kompleksno število vedno mogoče ločiti na njegove resnične in zapletene dele, lahko kompleksno število predstavljamo kot točko na dvodimenzionalni ravnini. Realni del kompleksnega števila je projekcija točke na stvarno os, imaginarni del števila pa projekcija na namišljeno os. Ko je kompleksno število predstavljeno kot vsota resničnih in namišljenih delov, rečemo, da je v pravokotne or algebraična oblika.
Naslednja slika prikazuje kompleksno število z = 2 + 4j
Polarna in eksponentna oblika
Kot je razvidno iz zgornje slike, bi lahko točko A predstavljali tudi dolžino puščice, r (imenovano tudi absolutna vrednost, velikost ali amplituda) in njen kot (ali faza), φ relativno v nasprotni smeri urinega kazalca do pozitivne vodoravne osi. To je polar obliki kompleksnega števila. Označuje se kot r ∠ φ.
Naslednji korak je zelo pomemben. V polarno obliko lahko zapišemo tudi kompleksno število eksponentna obrazec:
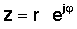
Ta preprost izraz je značilen po tem, da ima namizno število v eksponentu namesto običajnega realnega števila. Ta zapletena eksponenca se z dejanskim argumentom obnaša zelo drugače kot eksponentna funkcija. Medtem ko ex hitro narašča v obsegu za povečanje x> 0 in zmanjšanje za x <0, funkcija 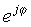
Eulerova formula zagotavlja povezovalno povezavo med pravokotnimi, polarnimi in eksponentnimi oblikami kompleksnih števil:
z = x + jy = ponovno jφ = r (cos φ + j greh φ )
Kje 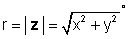
in φ = tan-1 (y / x).
Za naš zgornji primer, z = 2 + 4j:
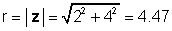
φ = tan-1 (4 / 2) = 63.4 °
zato 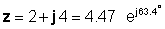
Ali obratno:
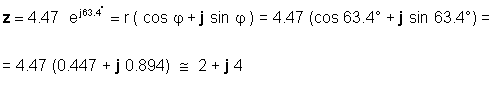
Pri uporabi obeh obrazcev boste morali biti spretni, odvisno od aplikacije. Na primer, seštevanje ali odštevanje je očitno lažje narediti, če so številke v pravokotni obliki, medtem ko je množenje in deljenje lažje storiti, če so števila v eksponentni obliki.
Operacije s kompleksnimi številkami
Operacije, ki jih lahko izvedemo s kompleksnimi števili, so podobne operacijam za realna števila. Spodaj so povzeta pravila in nekatere nove definicije.
Operacije z j
Operacije z j izhaja iz opredelitve imaginarne enote,


Če želite delati hitro in natančno, si morate zapomniti ta pravila:
j 2 = -1
j 3 =-j
j 4 =1
1/j = -j
j2 = -1 preprosto izhaja iz definicije 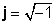
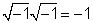
Za 1 /j, pomnožimo 1 /jby j / j = 1 in dobite j/ (jj) = j / (- 1) = -j.
Kompleksni konjugat
Kompleksno konjugat kompleksnega števila je enostavno izpeljati in je zelo pomemben. Za pridobitev kompleksnega konjugata kompleksnega števila v pravokotni obliki preprosto spremenite znak imaginarnega dela. Če želite to narediti za številko v eksponentni obliki, spremenite znak kota kompleksnega števila in hkrati ohranite njegovo absolutno vrednost.
Kompleksna konjugata kompleksnega števila z pogosto označuje z*.
Glede na kompleksno število z= a + jb, njegovo kompleksno konjugat je z*= a– jb.
If z je podana v eksponentni obliki, 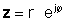
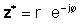
Z uporabo zgornjih definicij je enostavno videti, da kompleksno število, pomnoženo s kompleksnim konjugatom, daje kvadrat absolutne vrednosti kompleksnega števila:
zz* = r2 = a2 + b2
Tudi z dodajanjem ali odštevanjem kompleksnega števila in njegovega konjugata dobimo naslednje relacije:
z + z * = 2a
zato
Re (z) = a = ( z + z * ) / 2
Podobno:
z - z * =j2b
zato
Sem(z) = b = ( z -z * ) / 2j
Dokaz:
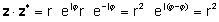
ali pomnožitev realnega in namišljenega dela in uporabo j2= -1
zz* = (a + jb) (a - jb) = a2+a jb - a jb - jbjb = a2j2 = a2 + b2
z + z* = a + jb + a - jb = 2a
z - z*= a + jb - a + jb =j2b
Številčni primeri:
V pravokotni obliki:
z = 3 + j4
z* = 3– j4
zz * = 9 + 16 = 25
V polarni obliki
z = 5 ∠ 53.13 °
z * = 5 ∠ - 53.13 °
V eksponentni obliki:
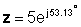
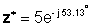
Seštevanje in odštevanje
Seštevanje in odštevanje zapletenih števil je enostavno - resnične in namišljene dele moramo le sešteti ločeno. Na primer, če
z1 = 3 - 4j in z2 = 2 + 3j
POTEM
z1 + z2 = 3 - 4j + 2 + 3j = 3 + 2 - 4j + 3j = 5 - j
z1 - z2 = 3 - 4j - 2 - 3j = 3 - 2 - 4j - 3j = 1 - j7
Očitno bi morali za te operacije uporabiti pravokotno obliko. Če so številke podane v eksponentni ali polarni obliki, jih moramo najprej spremeniti v pravokotno obliko po Eulerjevi formuli, kot je bila navedena prej.
Množenje
Obstajata dve metodi za množenje kompleksnih števil -
Množenje kompleksnih števil v pravokotni obliki
Če želite izvesti operacijo, preprosto pomnožite resnične in namišljene dele ene številke s stvarnimi in namišljenimi deli druge številke in uporabite identiteto j2 = -1.
z1z2 = (a1 + jb1) (a2 + jb2) = a1 a2 + jb1a2+ jb2a1 - b1b2 = a1 a2- b1b2 + j(b1a2+ jb2a1)
Če so kompleksna števila podana numerično, ni treba uporabiti zgornje formule. Na primer, pustite
z1 = 3 - 4j in z2 = 2 + 3j
Z neposrednim množenjem komponent:
z1z2 = (3 - 4j) (2 + 3j) = 6-8j +9j + 12 = 18 + j
ali z uporabo formule: z1z2 = a1 a2- b1b2 + j(b1a2+ b2a1)
z1z2 = 6 + 12 + j (-8 + 9) = 18 + j
Menimo, da je večja verjetnost napake, če uporabite formulo, kot če neposredno pomnožite komponente.
z1: = 3-4 * j
z2: = 2 + 3 * j
z1 * z2 = [18 + 1 * j]
uvozi matematiko kot m
uvozite cmath kot c
z1=kompleks('3-4j')
z2=kompleks('2+3j')
print(“z1*z2=”,z1*z2)
Množenje kompleksnih števil v polarni ali eksponentni obliki
Za izvedbo te operacije pomnožite absolutne vrednosti in dodajte kote dveh kompleksnih števil. Naj:
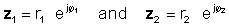
Potem z uporabo pravila množenja eksponentnih funkcij:
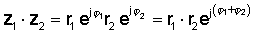
ali v polarni obliki
z1 z2 = r1 r2 ∠ φ1 + φ2
Opomba: To pravilo smo že uporabili, ko smo izračunali zz *nad. Ker ima kot konjugata nasprotni znak prvotnega kota, je kompleksno število, pomnoženo z lastnim veznikom, vedno resnično število; in sicer kvadrat njegove absolutne vrednosti: zz * = r2
Na primer:
z1 = 5 ∠ 30 ° in z2 = 4 ∠ -60 °
POTEM
z1z2 = 20 ∠ -30 °
ali v eksponentni obliki
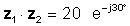
Množenje je očitno preprostejše, če so številke v polarni ali eksponentni obliki.
Če pa so zapletena števila navedena v pravokotni obliki, morate razmisliti o izvedbi množenja neposredno, kot je prikazano zgoraj, saj obstajajo dodatni koraki, če številke pretvorite v polarno obliko, preden jih pomnožite. Drugi dejavnik, ki ga je treba upoštevati, je, ali želite, da so odgovori v pravokotni obliki ali v polarni / eksponentni obliki. Na primer, če sta obe številki v pravokotni obliki, vendar želite, da je njihov izdelek v polarni obliki, jih je smiselno takoj pretvoriti in nato pomnožiti.
delitev
Obstajata dve metodi za delitev kompleksnih števil -
Delitev kompleksnih števil v pravokotni obliki
Za izvedbo operacije pomnožite števec in imenovalec s konjuktorjem imenovalca. Imenovalec postane resnično število in delitev se zmanjša na množenje dveh kompleksnih števil in delitev z dejanskim številom, kvadratom absolutne vrednosti imenovalca.
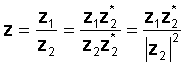
Na primer:
z1 = 3 - 4j in z2 = 2 + 3j
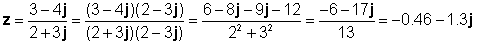
Preverimo ta rezultat s tolmačem TINA:
z1: = 3-4 * j
z2: = 2 + 3 * j
z1 / z2 = [- 461.5385m-1.3077 * j]
uvozi matematiko kot m
uvozite cmath kot c
z1=kompleks('3-4j')
z2=kompleks('2+3j')
natisni(“z1/z2=”,z1/z2)
Delitev kompleksnih števil v polarni ali eksponentni obliki
Za izvedbo operacije razdelite absolutne vrednosti (magnitude) in od kota števca odštejte kot imenovalca. Naj:
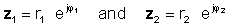
nato uporabimo pravilo delitve eksponentnih funkcij
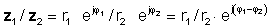
ali v polarni obliki
z 1 / z2 = r1 / r2 ∠ φ 1- φ 2
Na primer:
z 1 = 5 ∠ 30 ° in z 2 = 2 ∠ -60 °
POTEM
z 1 / z2 = 2.5 ∠ 90 °
ali v eksponentnih in pravokotnih oblikah
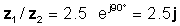
Preverimo ta rezultat s tolmačem TINA:
z1: = 5 * exp (j * degtorad (30))
z2: = 2 * exp (j * degtorad (-60))
z1 / z2 = [0 + 2.5 * j]
uvozi matematiko kot m
uvozite cmath kot c
z1=5*(c.exp(kompleksno(0,m.radianov(30))))
z2=2*(c.exp(kompleks(0,m.radiani(-60))))
natisni(“z1/z2=”,z1/z2)
Delitev je očitno preprostejša, če so številke v polarni ali eksponentni obliki.
Če pa so kompleksna števila navedena v pravokotni obliki, morate razmisliti o izvedbi delitve neposredno z uporabo metode zapletenega konjugata, kot je prikazano zgoraj, saj obstajajo dodatni koraki, če številke pretvorite v polarno obliko, preden jih delite. Drugi dejavnik, ki ga je treba upoštevati, je, ali želite, da so odgovori v pravokotni obliki ali v polarni / eksponentni obliki. Na primer, če sta obe številki v pravokotni obliki, vendar želite, da je njihov količnik v polarni obliki, je smiselno, da jih takoj pretvorite in nato razdelite.
Sedaj ponazorimo uporabo kompleksnih števil z več numeričnimi problemi. Kot ponavadi bomo preverili naše rešitve s pomočjo TINA-jevega tolmača. Interpreter deluje z radiani, vendar ima standardne funkcije za pretvorbo radianov v stopnje ali obratno.
Primer 1 Poišči polarno predstavitev:
z = 12 - j 48
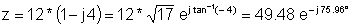
z: = 12-j * 48;
abs (z) = [49.4773]
arc (z) = [- 1.3258]
radtodeg (arc (z)) = [- 75.9638]
uvozi matematiko kot m
uvozite cmath kot c
z=12-kompleks(48j)
natisni ("abs(z)=",abs(z))
natisni("lok(z)=",c.faza(z))
print(“stopinj(lok(z))=”,m.stopinj(c.faza(z)))
Primer 2 Poiščite pravokotno predstavitev:
z = 25 e j 125 °
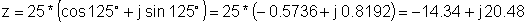
z: = 25 * exp (j * (degtorad (125)));
z = [- 14.3394 + 20.4788 * j]
Re (z) = [- 14.3394]
Im (z) = [20.4788]
uvozi matematiko kot m
uvozite cmath kot c
z=25*c.exp(kompleksno(0,m.radianov(125)))
natisni(“z=”,z)
natisni(“real(z)=”,z.real)
print(“imag(z)=”,z.imag)
Primer 3 Poišči polarno predstavitev naslednjih kompleksnih števil:
z 1 = 12 + j 48 z2 = 12 - j48 z3= -12 + j 48 z4= -12 - j 48
Absolutne vrednosti vseh štirih števil so enake, ker je absolutna vrednost neodvisna od znakov. Samo koti so različni.
z1: = 12 + j * 48;
abs (z1) = [49.4773]
arc (z1) = [1.3258]
radtodeg (arc (z1)) = [75.9638]
z2: = 12-j * 48;
abs (z2) = [49.4773]
arc (z2) = [- 1.3258]
radtodeg (arc (z2)) = [- 75.9638]
z3: = - 12 + j * 48;
abs (z3) = [49.4773]
arc (z3) = [1.8158]
radtodeg (arc (z3)) = [104.0362]
z4: = - 12-j * 48:
abs (z4) = [49.4773]
arc (z4) = [- 1.8158]
radtodeg (arc (z4)) = [- 104.0362]
uvozi matematiko kot m
uvozite cmath kot c
z1=kompleks('12+48j')
print("abs(z1)=",abs(z1))
natisni("lok(z1)=",c.faza(z1))
print(“stopinj(lok(z1))=”,m.stopinj(c.faza(z1)))
z2=kompleks('12-48j')
print("abs(z2)=",abs(z2))
natisni("lok(z2)=",c.faza(z2))
print(“stopinj(lok(z2))=”,m.stopinj(c.faza(z2)))
z3=kompleks('-12+48j')
print("abs(z3)=",abs(z3))
natisni("lok(z3)=",c.faza(z3))
print(“stopinj(lok(z3))=”,m.stopinj(c.faza(z3)))
z4=kompleks('-12-48j')
print("abs(z4)=",abs(z4))
natisni("lok(z4)=",c.faza(z4))
print(“stopinj(lok(z4))=”,m.stopinj(c.faza(z4)))
TINA funkcija lok () določa kot katerega koli kompleksnega števila in ga samodejno pravilno postavi v enega od štirih kvadrantov.
Bodite previdni, vendar s tan-1 funkcija za iskanje kota, saj je omejena na povratne kote samo v prvem in četrtem kvadrantu (–90 °φ<90 °).
Od leta z1 se nahaja v prvem kvadrantu koordinatnega sistema, izračun je:
α 1 = tan-1(48 / 12) = tan-1(4) = 75.96 °
Od leta z4 se nahaja v tretjem kvadrantu koordinatnega sistema, tan-1ne vrne pravilno kota. Izračun kota je:
α 4 = 180 ° + 75.96 ° = 255.96 ° ali -360 ° + 255.96 ° = - 104.04 °, kar je enako, kot je izračunala TINA.
z2 se nahaja v četrtem kvadrantu koordinatnega sistema. Izračun kota je:
α 2 = tan-1(-48 / 12) = tan-1(-4) = -75.96 °
z3, Vendar pa je v kvadrantu 2nd koordinatnega sistema, tako tan-1 ne vrne pravilno kota. Izračun kota je:
α 3 = 180 ° -75.96 ° = 104.04 °.
Primer 4 Imamo dve kompleksni številki: z1= 4 - j 6 in z2 = 5 ej45 ° .
Najdi z3 = z1 + z2; z4 = z1 - z2; z5 = z1 * z2; z6 = z1 / z2
Najprej rešimo problem s pomočjo TINA-jevega tolmača
{Rešitev TINA-jevega tolmača} |
Opazite, kako TINA brez težav ravna z dvema kompleksnima številkama v različnih oblikah.
Rešitev je brez tolmača bolj zapletena. Da bomo lahko primerjali različne metode množenja in delitve, bomo najprej določili polarno obliko z1 in pravokotno obliko z2 .
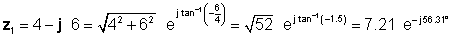
Nato najdemo štiri rešitve, pri čemer najprej uporabimo najlažje oblike: pravokotne za seštevanje in odštevanje ter eksponentno za množenje in deljenje:
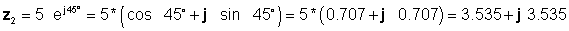
z 3 = z1 + z2 = 4 - j 6 + 3.535 + j 3.535 = 7.535 - j2.465
z 4 = z1 - z2 = 4 - j 6 - 3.535 - j 3.535 = 0.465 - j9.535
z 5 = z1 * z2 = 7.21 * 5 * ej(-56.31 ° + 45 °) = 36.05 e -j11.31 ° = 36.03 * (cos (-11.31 °) +j* sin (-11.31 °))
z 5 = 35.33 - j 7.07
z 6 = z1/z2= (7.21 / 5) * e j (-56.31 ° -45 °) = 1.442 e - j 101.31 ° = 1.442 (cos (-101.31 °) +j* sin (-101.31 °))
z 6 = -0.2828 - j 1.414
ki se strinjajo z rezultati tolmača TINA.
Množenje, izvedeno v pravokotni obliki:
z 5 =z1*z2 = (4-j6) * 3.535 * (1 +j) = 7.07 * (2-j3) * (1 +j) = 7.07 * (2-j3+j2 + 3) = 7.07 * (5-j) = 35.35-j7.07
Končno je bila delitev izvedena v pravokotni obliki:
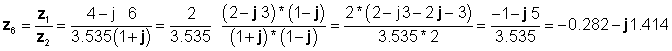
ki se strinjajo s predhodnimi rezultati.

