 Κάντε κλικ ή επιλέξτε τα παρακάτω κυκλώματα Παράδειγμα για να καλέσετε το TINACloud και επιλέξτε τη λειτουργία Interactive DC to Analyze them Online.
Κάντε κλικ ή επιλέξτε τα παρακάτω κυκλώματα Παράδειγμα για να καλέσετε το TINACloud και επιλέξτε τη λειτουργία Interactive DC to Analyze them Online. Πάρτε μια χαμηλού κόστους πρόσβαση στο TINACloud για να επεξεργαστείτε τα παραδείγματα ή να δημιουργήσετε τα δικά σας κυκλώματα
Σε αυτό και στα επόμενα κεφάλαια, θα παρουσιάσουμε ένα πολύ σημαντικό θέμα: AC ή εναλλασσόμενο ρεύμα. Το όνομα εναλλασσόμενου ρεύματος δεν είναι πολύ ακριβές και συνήθως καλύπτει κυκλώματα με ημιτονοειδή τάσεις και ρεύματα. Ωστόσο, εναλλασσόμενο ρεύμα μπορεί επίσης να σημαίνει οποιαδήποτε αυθαίρετη κυματομορφή ρεύματος. Η σημασία της εναλλασσόμενης τάσης είναι ότι αυτή η τάση χρησιμοποιείται για την κύρια πηγή ηλεκτρικής ενέργειας στα σπίτια και τη βιομηχανία σε όλο τον κόσμο. Είναι επίσης η βάση για πολλές εφαρμογές ηλεκτρονικών, τηλεπικοινωνιών και βιομηχανίας.
Για να χειριστούμε τις ημιτονοειδείς κυματομορφές και τα κυκλώματα που συνδέονται με αυτά, θα χρησιμοποιήσουμε μια απλή και κομψή μέθοδο που ονομάζεται μέθοδος των φασσάρων. Οι Phasors βασίζονται στις ιδιότητες των πολύπλοκων αριθμών, οι οποίοι είναι ιδανικοί για την αναπαραγωγή των ημιτονοειδών ποσοτήτων. Σε αυτό το κεφάλαιο, θα συνοψίσουμε τα βασικά γεγονότα σχετικά με τους πολύπλοκους αριθμούς και τις λειτουργίες τους. Θα δείξουμε επίσης πώς ο Διερμηνέας της TINA διευκολύνει τους υπολογισμούς με σύνθετους αριθμούς.
Οι σύνθετοι αριθμοί αποτελούνται από δύο μέρη, α πραγματικό μέρος (x), που είναι ένας πραγματικός αριθμός, και ένα λεγόμενο φανταστικό μέρος (y), που είναι ένας πραγματικός αριθμός πολλαπλασιασμένος με 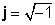
z = x + jy
όπου 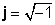
Παραδείγματα σύνθετων αριθμών:
z 1 = 1 + j
z 2 = 4-2 j
z 3 = 3- 5j
Οι σύνθετοι αριθμοί εισήχθησαν αρχικά τον δέκατο έβδομο αιώνα για να αντιπροσωπεύσουν τις ρίζες των πολυωνύμων που δεν μπορούσαν να αναπαρασταθούν μόνο με πραγματικούς αριθμούς. Για παράδειγμα, οι ρίζες της εξίσωσης x2 + 2x + 2 = 0 μπορεί να περιγραφεί μόνο ως 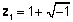
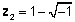
Γεωμετρική αναπαράσταση σύνθετων αριθμών
Ορθογώνια μορφή
Επειδή ένας πολύπλοκος αριθμός μπορεί πάντα να χωριστεί στα πραγματικά και σύνθετα μέρη του, μπορούμε να αντιπροσωπεύσουμε έναν πολύπλοκο αριθμό ως σημείο σε ένα δισδιάστατο επίπεδο. Το πραγματικό μέρος ενός σύνθετου αριθμού είναι η προβολή του σημείου στον πραγματικό άξονα, και το φανταστικό μέρος του αριθμού είναι η προβολή στον φανταστικό άξονα. Όταν ένας σύνθετος αριθμός αντιπροσωπεύεται ως το άθροισμα των πραγματικών και φανταστικών τμημάτων, λέμε ότι είναι ορθογώνιος or αλγεβρική μορφή.
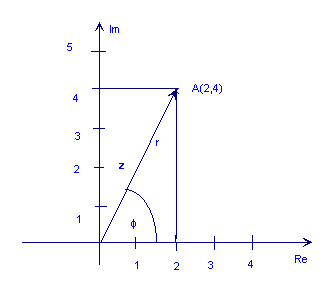
Το παρακάτω σχήμα δείχνει τον περίπλοκο αριθμό z = 2 + 4j
Πολική και εκθετική μορφή
Όπως μπορείτε να δείτε από το παραπάνω σχήμα, το σημείο Α θα μπορούσε επίσης να αντιπροσωπεύεται από το μήκος του βέλους, r (ονομάζεται επίσης απόλυτη τιμή, μέγεθος ή πλάτος) και η γωνία του (ή φάση), φ σχετική προς την αριστερόστροφη κατεύθυνση προς τον θετικό οριζόντιο άξονα. Αυτό είναι το πολικός μορφή ενός σύνθετου αριθμού. Συμβολίζεται ως r ∠ φ.
Το επόμενο βήμα είναι πολύ σημαντικό. Πολύπλοκος αριθμός σε πολική μορφή μπορεί επίσης να γραφτεί εκθετικός μορφή:
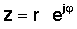
Αυτή η απλή έκφραση είναι διακριτική στο ότι έχει έναν φανταστικό αριθμό στον εκθέτη αντί για τον συνηθισμένο πραγματικό αριθμό. Αυτό το σύνθετο εκθετικό συμπεριφέρεται πολύ διαφορετικά από την εκθετική συνάρτηση με ένα πραγματικό όρισμα. Ενώ εx μεγαλώνει γρήγορα σε μέγεθος για αύξηση x> 0 και μειώνεται για το x <0, η συνάρτηση 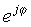
Ο τύπος του Euler παρέχει έναν ενωτικό σύνδεσμο ανάμεσα στις ορθογώνιες, πολικές και εκθετικές μορφές σύνθετων αριθμών:
z = x + jy = re jφ = r (cos φ + j αμαρτία φ )
όπου 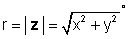
και φ = μαύρισμα-1 (γ / χ).
Για το παραπάνω παράδειγμα, z = 2 + 4j:
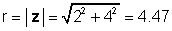
φ = μαύρισμα-1 (4 / 2) = 63.4 °
επομένως 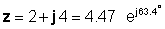
Ή το αντίστροφο:
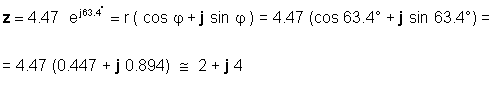
Θα πρέπει να είστε εξοικειωμένοι με τη χρήση και των δύο εντύπων, ανάλογα με την εφαρμογή. Για παράδειγμα, η προσθήκη ή η αφαίρεση είναι προφανώς πιο εύκολο να γίνουν όταν οι αριθμοί είναι σε ορθογώνια μορφή, ενώ ο πολλαπλασιασμός και η διαίρεση είναι ευκολότερο να γίνουν όταν οι αριθμοί είναι σε εκθετική μορφή.
Λειτουργίες με σύνθετους αριθμούς
Οι λειτουργίες που μπορούν να γίνουν με πολύπλοκους αριθμούς είναι παρόμοιες με αυτές για πραγματικούς αριθμούς. Οι κανόνες και ορισμένοι νέοι ορισμοί συνοψίζονται παρακάτω.
Λειτουργίες με j
Οι λειτουργίες με j απλά ακολουθήστε από τον ορισμό της φανταστικής μονάδας,


Για να μπορείτε να εργάζεστε γρήγορα και με ακρίβεια, θα πρέπει να απομνημονεύσετε αυτούς τους κανόνες:
j 2 = -1
j 3 =-j
j 4 =1
1/j = -j
j2 = -1 απλά προκύπτει από τον ορισμό του 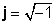
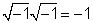
Για το 1 /j, πολλαπλασιάζουμε το 1 /jby j / j = 1 και πάρτε j/ (jj) = j / (- 1) = -j.
Σύνθετο συζυγές
Το σύνθετο συζυγές ενός σύνθετου αριθμού προέρχεται εύκολα και είναι πολύ σημαντικό. Για να αποκτήσετε το περίπλοκο συζυγές ενός σύνθετου αριθμού σε ορθογώνια μορφή, απλά αλλάξτε το σημάδι του φανταστικού μέρους. Για να το κάνετε για έναν αριθμό σε εκθετική μορφή, αλλάξτε το σημάδι της γωνίας του σύνθετου αριθμού διατηρώντας παράλληλα την απόλυτη τιμή του ίδιου.
Το σύνθετο συζυγές ενός σύνθετου αριθμού z συχνά υποδηλώνεται από z*.
Δεδομένου του πολύπλοκου αριθμού z= a + jb, το σύνθετο συζυγές του είναι z*= a- jb.
If z δίνεται σε εκθετική μορφή, 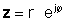
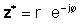
Χρησιμοποιώντας τους παραπάνω ορισμούς, είναι εύκολο να δούμε ότι ένας πολύπλοκος αριθμός πολλαπλασιασμένος με το περίπλοκο συζυγές του δίνει το τετράγωνο της απόλυτης τιμής του σύνθετου αριθμού:
zz* = r2 = α2 + b2
Επίσης, προσθέτοντας ή αφαιρώντας κάθε πολύπλοκο αριθμό και το συζυγές του, έχουμε τις ακόλουθες σχέσεις:
z + z * = 2a
επομένως
Re (z) = a = ( z + z * ) / 2
Ομοίως:
z - z * =j2b
επομένως
Im (z) = b = ( z -z * ) / 2j
Απόδειξη:
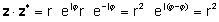
ή πολλαπλασιάζοντας τα πραγματικά και φανταστικά μέρη και τη χρήση j2= -1
zz* = (α + jβ) (α - jβ) = α2+a jβ - α jβ - jbjb = α2j2 = α2 + b2
z + z* = a + jb + a - jb = 2a
ζ - ζ*= a + jβ - α + jb =j2b
Αριθμητικά παραδείγματα:
Σε ορθογώνια μορφή:
z = 3 + j4
z* = 3- j4
zz * = 9 + 16 = 25
Σε πολική μορφή
z = 5 ∠ 53.13 °
z * = 5 ∠- 53.13 °
Σε εκθετική μορφή:
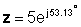
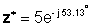
Πρόσθεση και αφαίρεση
Η προσθήκη και η αφαίρεση σύνθετων αριθμών είναι απλή - πρέπει να προσθέσουμε μόνο τα πραγματικά και φανταστικά μέρη ξεχωριστά. Για παράδειγμα, εάν
z1 = 3 - 4j και z2 = 2 + 3j
τότε
z1 + z2 = 3 - 4j + 2 + 3j = 3 + 2 - 4j + 3j = 5 - j
z1 - z2 = 3 - 4j - 2 - 3j = 3 - 2 - 4j - 3j = 1 - j7
Προφανώς, πρέπει να χρησιμοποιήσουμε την ορθογώνια φόρμα για αυτές τις λειτουργίες. Εάν οι αριθμοί δίνονται σε εκθετική ή πολική μορφή, θα πρέπει να τους μετατρέψουμε πρώτα σε ορθογώνια μορφή χρησιμοποιώντας τον τύπο του Euler, όπως αναφέρθηκε προηγουμένως.
Πολλαπλασιασμός
Υπάρχουν δύο μέθοδοι για πολλαπλασιασμό πολύπλοκων αριθμών–
Πολλαπλασιασμός σύνθετων αριθμών που έχουν δοθεί σε ορθογώνια μορφή
Για να εκτελέσετε τη λειτουργία, πολλαπλασιάστε απλά τα πραγματικά και φανταστικά μέρη ενός αριθμού με τη σειρά με τα πραγματικά και φανταστικά μέρη του άλλου αριθμού και χρησιμοποιήστε την ταυτότητα j2 = -1.
z1z2 = (α1 + jb1) (ένα2 + jb2) = α1 a2 + jb1a2+ jb2a1 - β1b2 = α1 a2- β1b2 + j(b1a2+ jb2a1)
Όταν οι σύνθετοι αριθμοί δίδονται αριθμητικά, δεν είναι απαραίτητο να χρησιμοποιήσετε τον παραπάνω τύπο. Για παράδειγμα, ας
z1 = 3 - 4j και z2 = 2 + 3j
Με άμεσο πολλαπλασιασμό των στοιχείων:
z1z2 = (3 - 4j) (2 + 3j) = 6- 8j +9j + 12 = 18 + j
ή χρησιμοποιώντας τον τύπο: z1z2 = α1 a2- β1b2 + j(b1a2+ β2a1)
z1z2 = 6 + 12 + j (-8 + 9) = 18 + j
Πιστεύουμε ότι είναι πιο πιθανό να προκαλέσετε σφάλμα εάν χρησιμοποιείτε τον τύπο απ 'ό, τι αν πολλαπλασιάσετε άμεσα τα εξαρτήματα.
z1: = 3-4 * j
z2: = 2 + 3 * j
z1 * z2 = [18 + 1 * j]
εισαγωγή μαθηματικών ως m
εισαγωγή cmath ως c
z1=complex('3-4j')
z2=complex('2+3j')
εκτύπωση("z1*z2=",z1*z2)
Πολλαπλασιασμός σύνθετων αριθμών που δίνονται σε πολική ή εκθετική μορφή
Για να εκτελέσετε αυτή τη λειτουργία, πολλαπλασιάστε τις απόλυτες τιμές και προσθέστε τις γωνίες των δύο σύνθετων αριθμών. Αφήνω:
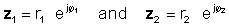
Στη συνέχεια, χρησιμοποιώντας τον κανόνα πολλαπλασιασμού των εκθετικών λειτουργιών:
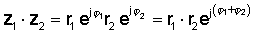
ή σε πολική μορφή
z1 z2 = r1 r2 Φ1 + φ2
Σημείωση: Έχουμε ήδη χρησιμοποιήσει αυτόν τον κανόνα όταν υπολογίσαμε zz *πάνω από. Δεδομένου ότι η γωνία του συζεύγματος έχει το αντίθετο σημάδι της αρχικής γωνίας, ένας πολύπλοκος αριθμός πολλαπλασιασμένος με το δικό του συζυγές είναι πάντα ένας πραγματικός αριθμός. δηλαδή, το τετράγωνο της απόλυτης τιμής του: zz * = r2
Για παράδειγμα, αφήστε:
z1 = 5 ∠ 30 ° και z2 = 4 ∠ -60 °
τότε
z1z2 = 20 ∠ -30 °
ή σε εκθετική μορφή
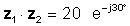
Ο πολλαπλασιασμός είναι προφανώς απλούστερος όταν οι αριθμοί βρίσκονται σε πολική ή εκθετική μορφή.
Ωστόσο, εάν οι σύνθετοι αριθμοί δίνονται σε ορθογώνια μορφή, θα πρέπει να εξετάσετε το ενδεχόμενο να εκτελέσετε τον πολλαπλασιασμό απευθείας όπως φαίνεται παραπάνω, καθώς υπάρχουν πρόσθετα βήματα εάν μετατρέψετε τους αριθμούς σε πολική μορφή πριν τον πολλαπλασιάσετε. Ένας άλλος παράγοντας που πρέπει να λάβετε υπόψη είναι αν θέλετε οι απαντήσεις να είναι σε ορθογώνια μορφή ή σε πολική / εκθετική μορφή. Για παράδειγμα, εάν οι δύο αριθμοί είναι σε ορθογώνια μορφή, αλλά θέλετε το προϊόν τους σε πολική μορφή, είναι λογικό να τα μετατρέψετε αμέσως και στη συνέχεια να τα πολλαπλασιάσετε.
διαίρεση
Υπάρχουν δύο μέθοδοι για τον διαχωρισμό των σύνθετων αριθμών
Κατανομή σύνθετων αριθμών σε ορθογώνια μορφή
Για να εκτελέσετε τη λειτουργία, πολλαπλασιάστε τον αριθμητή και τον παρονομαστή με το συζεύκτη του παρονομαστή. Ο παρονομαστής γίνεται πραγματικός αριθμός και η διαίρεση μειώνεται στον πολλαπλασιασμό δύο πολύπλοκων αριθμών και μια διαίρεση με έναν πραγματικό αριθμό, το τετράγωνο της απόλυτης τιμής του παρονομαστή.
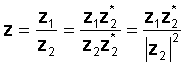
Για παράδειγμα αφήστε:
z1 = 3 - 4j και z2 = 2 + 3j
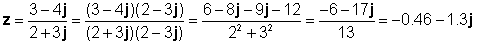
Ας ελέγξουμε αυτό το αποτέλεσμα με τον διερμηνέα της TINA:
z1: = 3-4 * j
z2: = 2 + 3 * j
z1 / z2 = [- 461.5385m-1.3077 * j]
εισαγωγή μαθηματικών ως m
εισαγωγή cmath ως c
z1=complex('3-4j')
z2=complex('2+3j')
εκτύπωση("z1/z2=",z1/z2)
Κατανομή σύνθετων αριθμών σε πολική ή εκθετική μορφή
Για να εκτελέσετε τη λειτουργία, διαιρέστε τις απόλυτες τιμές (μεγέθη) και αφαιρέστε τη γωνία του παρανομαστή από τη γωνία του αριθμητή. Αφήνω:
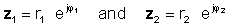
στη συνέχεια, χρησιμοποιώντας τον κανόνα κατανομής εκθετικών λειτουργιών
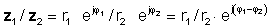
ή σε πολική μορφή
z 1 / z2 = r1 / r2 ∠ φ 1- φ 2
Για παράδειγμα, αφήστε:
z 1 = 5 ∠ 30 ° και z 2 = 2 ∠ -60 °
τότε
z 1 / z2 = 2.5 ∠ 90 °
ή σε εκθετικές και ορθογώνιες μορφές
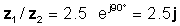
Ας ελέγξουμε αυτό το αποτέλεσμα με τον διερμηνέα της TINA:
z1: = 5 * exp (j * degtorad (30))
z2: = 2 * exp (j * degtorad (-60))
z1 / z2 = [0 + 2.5 * j]
εισαγωγή μαθηματικών ως m
εισαγωγή cmath ως c
z1=5*(c.exp(complex(0,m.radians(30))))
z2=2*(c.exp(complex(0,m.radians(-60))))
εκτύπωση("z1/z2=",z1/z2)
Η διαίρεση είναι προφανώς απλούστερη όταν οι αριθμοί είναι σε πολική ή εκθετική μορφή.
Ωστόσο, εάν οι σύνθετοι αριθμοί δίδονται σε ορθογώνια μορφή, θα πρέπει να εξετάσετε το ενδεχόμενο να εκτελέσετε την διαίρεση απευθείας χρησιμοποιώντας τη σύνθετη μέθοδο συζεύγματος όπως φαίνεται παραπάνω, καθώς υπάρχουν επιπλέον βήματα εάν μετατρέψετε τους αριθμούς σε πολική μορφή πριν τους διαιρέσετε. Ένας άλλος παράγοντας που πρέπει να λάβετε υπόψη είναι αν θέλετε οι απαντήσεις να είναι σε ορθογώνια μορφή ή σε πολική / εκθετική μορφή. Για παράδειγμα, εάν οι δύο αριθμοί είναι σε ορθογώνια μορφή, αλλά θέλετε το πηλίκο τους σε πολική μορφή, είναι λογικό να τα μετατρέψετε αμέσως και στη συνέχεια να τα διαιρέσετε.
Τώρα ας δείξουμε τη χρήση σύνθετων αριθμών με περισσότερα αριθμητικά προβλήματα. Ως συνήθως, θα ελέγξουμε τις λύσεις μας χρησιμοποιώντας τον Διερμηνέα της TINA. Ο διερμηνέας λειτουργεί με ακτίνια, αλλά έχει τυπικές λειτουργίες για τη μετατροπή των ακτινών σε μοίρες ή αντίστροφα.
Παράδειγμα 1 Βρείτε την πολική αναπαράσταση:
z = 12 - j 48
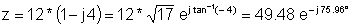
z: = 12-j * 48.
abs (z) = [49.4773]
τόξο (z) = [- 1.3258]
radtodeg (τόξο (z)) = [- 75.9638]
εισαγωγή μαθηματικών ως m
εισαγωγή cmath ως c
z=12-σύνθετο(48j)
print("abs(z)=",abs(z))
print("arc(z)=",c.phase(z))
print("degrees(arc(z))=",m.degrees(c.phase(z)))
Παράδειγμα 2 Βρείτε την ορθογώνια αναπαράσταση:
z = 25 e j 125 °
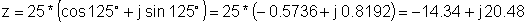
z: = 25 * exp (j * (degtorad (125))).
z = [- 14.3394 + 20.4788 * j]
Re (z) = [- 14.3394]
Im (z) = [20.4788]
εισαγωγή μαθηματικών ως m
εισαγωγή cmath ως c
z=25*c.exp(complex(0,m.radians(125)))
εκτύπωση(“z=”,z)
print("real(z)=",z.real)
print("imag(z)=",z.imag)
Παράδειγμα 3 Βρείτε την πολική αναπαράσταση των ακόλουθων σύνθετων αριθμών:
z 1 = 12 + j 48 z2 = 12 - j48 z3= -12 + j 48 z4= -12 - j 48
Οι απόλυτες τιμές και των τεσσάρων αριθμών είναι οι ίδιες επειδή η απόλυτη τιμή είναι ανεξάρτητη από τα σημάδια. Μόνο οι γωνίες είναι διαφορετικές.
z1: = 12 + j * 48.
abs (z1) = [49.4773]
τόξο (z1) = [1.3258]
radtodeg (τόξο (z1)) = [75.9638]
z2: = 12-j * 48;
abs (z2) = [49.4773]
τόξο (z2) = [- 1.3258]
radtodeg (τόξο (z2)) = [- 75.9638]
z3: = - 12 + j * 48;
abs (z3) = [49.4773]
τόξο (z3) = [1.8158]
radtodeg (τόξο (z3)) = [104.0362]
z4: = - 12-j * 48:
abs (z4) = [49.4773]
τόξο (z4) = [- 1.8158]
radtodeg (τόξο (z4)) = [- 104.0362]
εισαγωγή μαθηματικών ως m
εισαγωγή cmath ως c
z1=complex('12+48j')
print("abs(z1)=",abs(z1))
print("arc(z1)=",c.phase(z1))
print("degrees(arc(z1))=",m.degrees(c.phase(z1)))
z2=complex('12-48j')
print("abs(z2)=",abs(z2))
print("arc(z2)=",c.phase(z2))
print("degrees(arc(z2))=",m.degrees(c.phase(z2)))
z3=complex('-12+48j')
print("abs(z3)=",abs(z3))
print("arc(z3)=",c.phase(z3))
print("degrees(arc(z3))=",m.degrees(c.phase(z3)))
z4=complex('-12-48j')
print("abs(z4)=",abs(z4))
print("arc(z4)=",c.phase(z4))
print("degrees(arc(z4))=",m.degrees(c.phase(z4)))
Η λειτουργία τόξου TINA () καθορίζει τη γωνία οποιουδήποτε σύνθετου αριθμού, τοποθετώντας τον σωστά σε ένα από τα τέσσερα τεταρτημόρια.
Προσέξτε, ωστόσο, χρησιμοποιώντας το μαύρισμα-1 Λειτουργία για την εύρεση της γωνίας, καθώς περιορίζεται στην επιστροφή γωνιών μόνο στο πρώτο και τέταρτο τεταρτημόριο (–90 °φ<90 °).
Από z1 βρίσκεται στο πρώτο τεταρτημόριο του συστήματος συντεταγμένων, ο υπολογισμός είναι:
α 1 = μαύρισμα-1(48 / 12) = μαύρισμα-1(4) = 75.96 °
Από z4 βρίσκεται στο τρίτο τεταρτημόριο του συστήματος συντεταγμένων, tan-1δεν επιστρέφει τη γωνία σωστά. Ο υπολογισμός γωνίας είναι:
α 4 = 180 ° + 75.96 ° = 255.96 ° ή -360 ° + 255.96 ° = - 104.04 °, που είναι το ίδιο όπως υπολογίστηκε από την TINA.
z2 βρίσκεται στο τέταρτο τεταρτημόριο του συστήματος συντεταγμένων Ο υπολογισμός γωνίας είναι:
α 2 = μαύρισμα-1(-48 / 12) = μαύρισμα-1(-4) = -75.96 °
z3, Ωστόσο, βρίσκεται στο τετράγωνο 2nd του συστήματος συντεταγμένων, τόσο μαύρο-1 δεν επιστρέφει τη γωνία σωστά. Ο υπολογισμός γωνίας είναι:
α 3 = 180 ° -75.96 ° = 104.04 °.
Παράδειγμα 4 Έχουμε δύο σύνθετους αριθμούς: z1= 4 - j 6 και z2 = 5 ej45 ° .
Εύρεση z3 = z1 + z2; z4 = z1 - z2; z5 = z1 * z2; z6 = z1 / z2
Πρώτα λύνουμε το πρόβλημα χρησιμοποιώντας τον Διερμηνέα της TINA
{Λύση από τον διερμηνέα της TINA} |
Παρατηρήστε πώς η TINA χειρίζεται αβίαστα τους δύο σύνθετους αριθμούς που δίδονται με διαφορετικές μορφές.
Η λύση είναι πιο περίπλοκη χωρίς τον διερμηνέα. Για να συγκρίνουμε τις διαφορετικές μεθόδους πολλαπλασιασμού και διαίρεσης, θα καθορίσουμε πρώτα την πολική μορφή του z1 και την ορθογώνια μορφή του z2 .
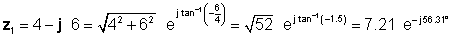
Στη συνέχεια, βρίσκουμε τις τέσσερις λύσεις χρησιμοποιώντας τις ευκολότερες φόρμες πρώτα: ορθογώνια για προσθήκη και αφαίρεση και εκθετική για πολλαπλασιασμό και διαίρεση:
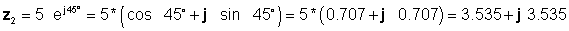
z 3 = z1 + z2 = 4 - j 6 + 3.535 + j 3.535 = 7.535 - j2.465
z 4 = z1 - z2 = 4 - j 6 - 3.535 - j 3.535 = 0.465 - j9.535
z 5 = z1 * z2 = 7.21 * 5 * ej(-56.31 ° + 45 °) = 36.05 e -j11.31 ° = 36.03 * (cos (-11.31 °) +j* αμαρτία (-11.31 °))
z 5 = 35.33 - j 7.07
z 6 = z1/z2= (7.21 / 5) * ε j (-56.31 ° -45 °) = 1.442 e - j 101.31 ° = 1.442 (cos (-101.31 °) +j* αμαρτία (-101.31 °))
z 6 = -0.2828 - j 1.414
που συμφωνούν με τα αποτελέσματα που έχουν αποκτηθεί με τον Διερμηνέα της TINA.
Ο πολλαπλασιασμός που πραγματοποιείται σε ορθογώνια μορφή:
z 5 =z1*z2 = (4-j6) * 3.535 * (1 +j) = 7.07 * (2-j3) * (1 +j) = 7.07 * (2-j3+j2 + 3) = 7.07 * (5-j) = 35.35-j7.07
Τέλος η διαίρεση πραγματοποιείται σε ορθογώνια μορφή:
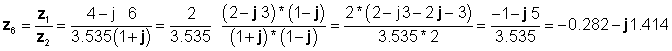
που συμφωνούν με τα προηγούμενα αποτελέσματα.

