Κάντε κλικ ή επιλέξτε τα παρακάτω κυκλώματα Παράδειγμα για να καλέσετε το TINACloud και επιλέξτε τη λειτουργία Interactive DC to Analyze them Online.
Κάντε κλικ ή επιλέξτε τα παρακάτω κυκλώματα Παράδειγμα για να καλέσετε το TINACloud και επιλέξτε τη λειτουργία Interactive DC to Analyze them Online. Πάρτε μια χαμηλού κόστους πρόσβαση στο TINACloud για να επεξεργαστείτε τα παραδείγματα ή να δημιουργήσετε τα δικά σας κυκλώματα
Ένας άλλος τρόπος απλούστευσης του πλήρους συνόλου των εξισώσεων του Kirchhoff είναι η τρέχουσα μέθοδος πλέγματος ή βρόχου. Χρησιμοποιώντας αυτήν τη μέθοδο, ο τρέχων νόμος του Kirchhoff ικανοποιείται αυτόματα και οι εξισώσεις βρόχου που γράφουμε ικανοποιούν επίσης τον νόμο περί τάσης του Kirchhoff. Η ικανοποίηση του ισχύοντος νόμου του Kirchhoff επιτυγχάνεται με την εκχώρηση κλειστών βρόχων ρεύματος που ονομάζονται ρεύματα πλέγματος ή βρόχου σε κάθε ανεξάρτητο βρόχο του κυκλώματος και χρησιμοποιώντας αυτά τα ρεύματα για να εκφράσουν όλες τις άλλες ποσότητες του κυκλώματος. Δεδομένου ότι τα ρεύματα βρόχου είναι κλειστά, το ρεύμα που ρέει σε έναν κόμβο πρέπει επίσης να ρέει έξω από τον κόμβο. έτσι η σύνταξη εξισώσεων κόμβου με αυτά τα ρεύματα οδηγεί στην ταυτότητα.
Ας εξετάσουμε πρώτα τη μέθοδο των ρευμάτων πλέγματος.
Αρχικά σημειώνουμε ότι η μέθοδος ρεύματος πλέγματος ισχύει μόνο για κυκλώματα «επίπεδου». Τα επίπεδα κυκλώματα δεν έχουν καλώδια διέλευσης όταν σχεδιάζονται σε αεροπλάνο. Συχνά, σχεδιάζοντας ξανά ένα κύκλωμα που φαίνεται να είναι μη επίπεδο, μπορείτε να προσδιορίσετε ότι είναι, στην πραγματικότητα, επίπεδο. Για μη επίπεδα επίπεδα, χρησιμοποιήστε το τρέχουσα μέθοδο βρόχου που περιγράφονται παρακάτω σε αυτό το κεφάλαιο.
Για να εξηγήσετε την ιδέα των ρευμάτων πλέγματος, φανταστείτε τα κλαδιά του κυκλώματος ως «δίχτυ ψαρέματος» και αντιστοιχίστε ένα ρεύμα πλέγματος σε κάθε πλέγμα του διχτυού. (Μερικές φορές λέγεται επίσης ότι εκχωρείται ένας κλειστός βρόχος ρεύματος σε κάθε «παράθυρο» του κυκλώματος.)
  Το σχηματικό διάγραμμα 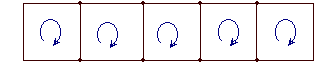  Το "δίχτυ αλιείας" ή το γράφημα του κυκλώματος |
Η τεχνική αναπαράστασης του κυκλώματος με ένα απλό σχέδιο, που ονομάζεται α γραφική παράσταση, είναι αρκετά ισχυρό. Από Οι νόμοι του Kirchhoff δεν εξαρτώνται από τη φύση των συστατικών, μπορείτε να αγνοήσετε τα συγκεκριμένα στοιχεία και να τα αντικαταστήσετε με απλά τμήματα γραμμής, που ονομάζονται υποκαταστήματα του γραφήματος. Η αναπαράσταση κυκλωμάτων με γραφήματα μας επιτρέπει να χρησιμοποιήσουμε τις τεχνικές των μαθηματικών θεωρία γραφημάτων. Αυτό μας βοηθά να εξερευνήσουμε την τοπολογική φύση ενός κυκλώματος και να προσδιορίσουμε τους ανεξάρτητους βρόχους. Επιστρέψτε αργότερα σε αυτόν τον ιστότοπο για να διαβάσετε περισσότερα σχετικά με αυτό το θέμα.
Τα βήματα της ανάλυσης ρεύματος ματιών:
Αντιστοιχίστε ένα ρεύμα πλέγματος σε κάθε πλέγμα. Αν και η κατεύθυνση είναι αυθαίρετη, είναι συνηθισμένο να χρησιμοποιείται η φορά των δεικτών του ρολογιού.
Εφαρμόστε τον νόμο τάσης Kirchhoff (KVL) γύρω από κάθε πλέγμα, προς την ίδια κατεύθυνση με τα ρεύματα πλέγματος. Εάν μια αντίσταση έχει δύο ή περισσότερα ρεύματα πλέγματος μέσω αυτής, το συνολικό ρεύμα μέσω της αντίστασης υπολογίζεται ως το αλγεβρικό άθροισμα των ρευμάτων πλέγματος. Με άλλα λόγια, εάν ένα ρεύμα που ρέει μέσω της αντίστασης έχει την ίδια κατεύθυνση με το ρεύμα πλέγματος του βρόχου, έχει ένα θετικό σημάδι, διαφορετικά ένα αρνητικό σημάδι στο άθροισμα. Οι πηγές τάσης λαμβάνονται υπόψη ως συνήθως, Εάν η κατεύθυνση τους είναι ίδια με το ρεύμα πλέγματος, η τάση τους θεωρείται θετική, διαφορετικά αρνητική, στις εξισώσεις KVL. Συνήθως, για τρέχουσες πηγές, μόνο ένα ρεύμα πλέγματος ρέει μέσω της πηγής και το ρεύμα έχει την ίδια κατεύθυνση με το ρεύμα της πηγής. Εάν αυτό δεν συμβαίνει, χρησιμοποιήστε τη γενικότερη τρέχουσα μέθοδο βρόχου, που περιγράφεται αργότερα σε αυτήν την παράγραφο. Δεν χρειάζεται να γράφετε εξισώσεις KVL για βρόχους που περιέχουν ρεύματα πλέγματος που έχουν αντιστοιχιστεί σε τρέχουσες πηγές.
Λύστε τις προκύπτουσες εξισώσεις βρόχου για τα ρεύματα των ματιών.
Προσδιορίστε τυχόν απαιτούμενο ρεύμα ή τάση στο κύκλωμα χρησιμοποιώντας τα ρεύματα πλέγματος.
Ας δείξουμε τη μέθοδο με το ακόλουθο παράδειγμα:
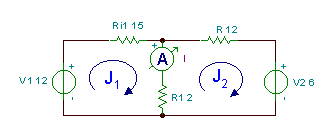
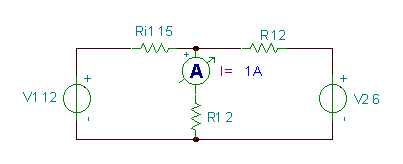
Βρείτε το τρέχον I στο κύκλωμα παρακάτω.
Βλέπουμε ότι υπάρχουν δύο πλέγματα (ή ένα αριστερό και δεξί παράθυρο) σε αυτό το κύκλωμα. Ας αντιστοιχίσουμε τα ρεύματα πλέγματος δεξιόστροφα J1 και J2 στα μάτια. Στη συνέχεια γράφουμε τις εξισώσεις KVL, εκφράζοντας τις τάσεις στις αντιστάσεις από τον νόμο του Ohm:
-V1 + J1* (Ri1+R1) - J2*R1 = 0
V2 - J1*R1 + J2* (R + R1) = 0
Αριθμητικά:
-12 + J1* 17 - J2* 2 = 0
6 - Ι1* 2 + J2* 14 = 0
Express J1 από την πρώτη εξίσωση: J1 = 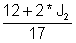

πολλαπλασιάστε με 17: 102 - 24 + 4 * J2 + 238 * J2 = 0 ως εκ τούτου J2 = 
και J1 = 
Τέλος, το απαιτούμενο ρεύμα:
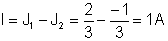
{Μέθοδος ρεύματος ματιών}
Sys J1, J2
J1*(Ri1+R1)-J2*R1-V1=0
J1*R1+J2*(R1+R)+V2=0
τέλος?
J1 = [666.6667m]
J2 = [- 333.3333m]
Ι: = J1-J2.
I = [1]
εισαγωγή numpy ως n
#Χρησιμοποιήστε τη μέθοδο ρεύματος πλέγματος!
#Έχουμε ένα γραμμικό σύστημα εξισώσεων που θέλουμε να λύσουμε
#για I1,I2:
#I1*(Ri1+R1)+I2*Ri1-V1=0
#-V1+I1*Ri1+I2*(Ri1+R)+V2=0
#Γράψτε τον πίνακα των συντελεστών:
A=n.array([[Ri1+R1,Ri1],[Ri1,Ri1+R]])
#Γράψτε τον πίνακα των σταθερών:
b=n.συστοιχία([V1,V1-V2])
x=n.linalg.solve(A,b)
I1=x[0]
I2=x[1]
print("I1= %.3f"%I1)
print("I2= %.3f"%I2)
I=I1
print("I= %.3f"%I)
Ας δούμε τα αποτελέσματα με την TINA:

Στη συνέχεια, ας λύσουμε ξανά το προηγούμενο παράδειγμα, αλλά με το πιο γενικό μέθοδος ρευμάτων βρόχου. Χρησιμοποιώντας αυτή τη μέθοδο, οι κλειστοί βρόχοι ρεύματος, που ονομάζονται ρεύματα βρόχου, εκχωρούνται όχι απαραίτητα στα πλέγματα του κυκλώματος, αλλά σε αυθαίρετα ανεξάρτητους βρόχους. Μπορείτε να βεβαιωθείτε ότι οι βρόχοι είναι ανεξάρτητοι έχοντας τουλάχιστον ένα στοιχείο σε κάθε βρόχο που δεν περιέχεται σε κανένα άλλο βρόχο. Για επίπεδα κυκλώματα, ο αριθμός των ανεξάρτητων βρόχων είναι ο ίδιος με τον αριθμό των ματιών, το οποίο είναι εύκολο να φανεί.
Ένας πιο ακριβής τρόπος προσδιορισμού του αριθμού των ανεξάρτητων βρόχων είναι ο εξής.
Δίνεται ένα κύκλωμα με b κλάδοι και N κόμβοι. Ο αριθμός των ανεξάρτητων βρόχων l είναι:
l = b - Ν + 1
Αυτό προκύπτει από το γεγονός ότι ο αριθμός των ανεξάρτητων εξισώσεων Kirchhoff πρέπει να είναι ίσος με τους κλάδους του κυκλώματος και ήδη γνωρίζουμε ότι υπάρχουν μόνο Ν-1 ανεξάρτητες εξισώσεις κόμβων. Επομένως, ο συνολικός αριθμός των εξισώσεων του Kirchhoff είναι
b = Ν-1 + l και ως εκ τούτου l = b - Ν + 1
Αυτή η εξίσωση προκύπτει επίσης από το θεμελιώδες θεώρημα της θεωρίας γραφημάτων που θα περιγραφεί αργότερα σε αυτόν τον ιστότοπο.
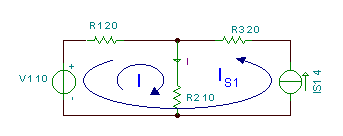
Τώρα ας λύσουμε ξανά το προηγούμενο παράδειγμα, αλλά πιο απλά, χρησιμοποιώντας τη μέθοδο loop current. Με αυτήν τη μέθοδο είμαστε ελεύθεροι να χρησιμοποιούμε βρόχους σε πλέγματα ή άλλους βρόχους, αλλά ας διατηρήσουμε τον βρόχο με το J1 στο αριστερό πλέγμα του κυκλώματος. Ωστόσο, για τον δεύτερο βρόχο επιλέγουμε τον βρόχο με J2, όπως φαίνεται στο παρακάτω σχήμα. Το πλεονέκτημα αυτής της επιλογής είναι ότι ο J1 θα είναι ίσο με το απαιτούμενο ρεύμα I, καθώς είναι το μόνο ρεύμα βρόχου που διέρχεται από το R1. Αυτό σημαίνει ότι δεν χρειάζεται να υπολογίσουμε το J2 καθόλου. Σημειώστε ότι, σε αντίθεση με τα "πραγματικά" ρεύματα, η φυσική έννοια των ρευμάτων βρόχου εξαρτάται από τον τρόπο που τα αντιστοιχίζουμε στο κύκλωμα.
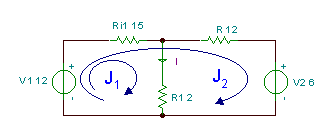

Οι εξισώσεις KVL:
J1 * (R1+Ri1) + J2 * R i1 - V1 = 0
-V1+ J1 * Ri1+ J2 * (R + Ri) + V2 = 0
και το απαιτούμενο ρεύμα: I = J1
Numerically: J1*(15+2)+J2*15-12 = 0
-12 + J1 * 15 + J2 * (15 + 12) + 6 = 0
Express J2 από τη δεύτερη εξίσωση:
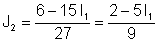
Αντικαταστήστε την πρώτη εξίσωση:
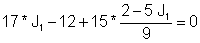
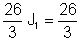
Ως εκ τούτου: J1 = I = 1 Α
Άλλα παραδείγματα.
Παράδειγμα 1
Βρείτε το τρέχον I στο κύκλωμα παρακάτω.
Σε αυτό το κύκλωμα, χρησιμοποιούμε τη μέθοδο των ρευμάτων βρόχου. Στο αριστερό παράθυρο του κυκλώματος παίρνουμε ένα ρεύμα βρόχου με το οποίο δηλώνουμε I δεδομένου ότι είναι ίσο με το ζητούμενο ρεύμα. Το άλλο ρεύμα βρόχου είναι ίσο με το ρεύμα πηγής Is1, οπότε το δηλώνουμε απευθείας ως IS1.
Σημειώστε ότι η κατεύθυνση αυτού του ρεύματος βρόχου είναι δεν δεξιόστροφα, καθώς η κατεύθυνση καθορίζεται από την τρέχουσα πηγή. Ωστόσο, δεδομένου ότι αυτό το ρεύμα βρόχου είναι ήδη γνωστό, δεν χρειάζεται να γράψετε την εξίσωση KVL για το βρόχο όπου IS1 είναι κατηλημμένο.
Επομένως, η μόνη εξίσωση που πρέπει να επιλυθεί είναι:
-V1 + Ι * R2 + R1 * (I - IS1) = 0
ως εκ τούτου
Ι = (V1 + R1 *IS1) / (R1 + R2)
Αριθμητικά
I=(10+20*4)/(20+10)=3 A
Μπορείτε επίσης να δημιουργήσετε αυτό το αποτέλεσμα καλώντας τη συμβολική ανάλυση της TINA από το μενού Ανάλυση / Συμβολική Ανάλυση / Αποτέλεσμα DC:
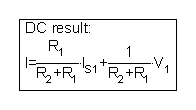
Ή μπορείτε να λύσετε την εξίσωση KVL από τον διερμηνέα:
| {Λύση από τον διερμηνέα της TINA} {Χρησιμοποιήστε την τρέχουσα μέθοδο πλέγματος} Sys I -V1 + I * R2 + R1 * (I - IS1) = 0 τέλος? I = [3] |
Το ακόλουθο παράδειγμα έχει 3 τρέχουσες πηγές και είναι πολύ εύκολο να επιλυθεί με τη μέθοδο των ρευμάτων βρόχου.
Παράδειγμα 2
Βρείτε την τάση V.
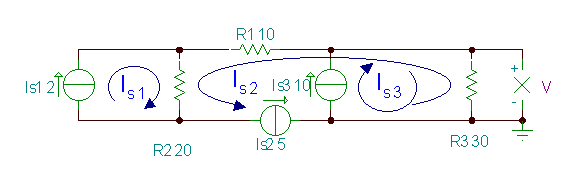

Σε αυτό το παράδειγμα, μπορούμε να επιλέξουμε τρία ρεύματα βρόχου έτσι ώστε το καθένα να περάσει μόνο από μια τρέχουσα πηγή. Επομένως, και τα τρία ρεύματα βρόχου είναι γνωστά και πρέπει να εκφράσουμε μόνο την άγνωστη τάση V χρησιμοποιώντας αυτά.
Κάνοντας το αλγεβρικό άθροισμα των ρευμάτων μέσω του R3:
V = (ΙS3 - ΕγώS2) * R3= (10-5) * 30 = 150 V. Μπορείτε να το επιβεβαιώσετε με το TINA :.
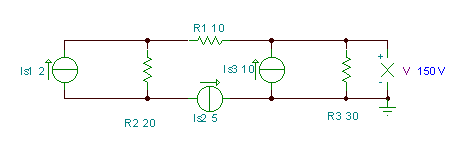

Στη συνέχεια, ας αντιμετωπίσουμε ξανά ένα πρόβλημα που έχουμε ήδη λύσει στο Οι νόμοι του Kirchhoff και Μέθοδος δυναμικού κόμβου Κεφάλαια.
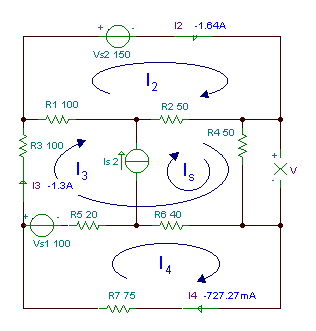
Παράδειγμα 3
Βρείτε την τάση V της αντίστασης R4.
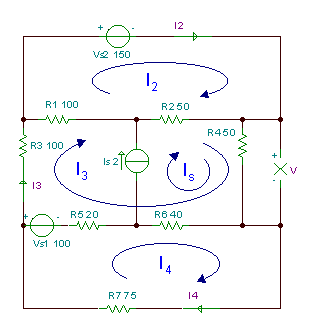

R1 = R3 = 100 ohm, R2 = R4 = 50 ohm, R5 = 20 ohm, R6 = 40 ohm, R7 = 75 ohm.
Αυτό το πρόβλημα χρειάστηκε τουλάχιστον 4 εξισώσεις για την επίλυση στα προηγούμενα κεφάλαια.
Επίλυση αυτού του προβλήματος με τη μέθοδο των ρευμάτων βρόχου, έχουμε τέσσερις ανεξάρτητους βρόχους, αλλά με τη σωστή επιλογή των ρευμάτων βρόχου, ένα από τα ρεύματα βρόχου θα είναι ίσο με το ρεύμα πηγής Is.
Με βάση τα ρεύματα βρόχου που φαίνονται στο παραπάνω σχήμα, οι εξισώσεις βρόχου είναι:
VS1+I4* (R5+R6+R7) - ΕΓΩS*R6 -ΕΓΩ3* (R5 + R6) = 0
VS2 - Εγώ3* (R1+R2) - ΕΓΩS*R2 + Ι2* (R1 + R2) = 0
-VS1 + Ι3* (R1 + R2 + R3 + R4 + R5 + R6) + ΙS* (R2 +R4 + R6) - ΕΓΩ4* (R5 + R6) - Εγώ2* (R1 + R2) = 0
Η άγνωστη τάση V μπορεί να εκφραστεί από τα ρεύματα βρόχου:
V = R4 * (ΕΓΩ2 + Ι3)
Αριθμητικά:
100 + I4* 135-2 * 40-I3* 60 = 0
150 + I2* 150-2 * 50-I3* 150 = 0
-100 + Ι3* 360 + 2 * 140-I4* 60-I2* 150 = 0
V = 50 * (2 + Ι3)
Μπορούμε να χρησιμοποιήσουμε τον κανόνα του Cramer για να λύσουμε αυτό το σύστημα εξισώσεων:
I4 = D3/D
όπου D είναι ο καθοριστικός παράγοντας του συστήματος. D4, ο καθοριστικός παράγοντας για το I4, σχηματίζεται αντικαθιστώντας τη δεξιά πλευρά του συστήματος τοποθετείται για τη στήλη του Ι4συντελεστές
Το σύστημα των εξισώσεων σε διαταγμένη μορφή:
- 60 * Ι3 + 135 * Ι4= -20
150 * I2-150 * Ι3 = - 50
-150 * Ι2+ 360 * Ι3 - 60 * Ι4= - 180
Ετσι το καθοριστικός D:
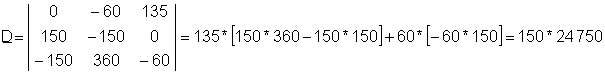
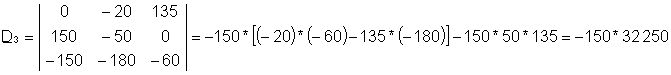
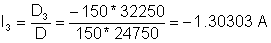
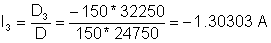
Η λύση αυτού του συστήματος εξισώσεων είναι:
V = R4* (2 + Ι3) = 34.8485 V
Μπορείτε να επιβεβαιώσετε την απάντηση μέσω του αποτελέσματος που υπολογίστηκε από την TINA.
Sys I2, I3, I4
Vs2+I2*(R1+R2)-R2*Is-I3*(R1+R2)=0
-Vs1+I3*(R1+R2+R3+R4+R5+R6)+Is*(R2+R4+R6)-I2*(R1+R2)-I4*(R5+R6)=0
Vs1+I4*(R5+R6+R7)-Is*R6-I3*(R5+R6)=0
τέλος?
I2 = [- 1.6364]
I3 = [- 1.303]
I4 = [- 727.2727m]
V: = R4 * (είναι + I3).
V = [34.8485]
εισαγωγή numpy ως n
#Έχουμε ένα γραμμικό σύστημα εξισώσεων που θέλουμε να λύσουμε
#για I1,I2,I3,I4:
#I1=Είναι
#Vs2+I2*(R1+R2)-R2*I1-I3*(R1+R2)=0
#-Vs1+I3*(R1+R2+R3+R4+R5+R6)+I1*(R2+R4+R6)-I2*(R1+R2)-I4*(R5+R6)=0
#Vs1+I4*(R5+R6+R7)-I1*R6-I3*(R5+R6)=0
#Γράψτε τον πίνακα των συντελεστών:
A=n.array([[1,0,0,0],[-R2,R1+R2,-(R1+R2),0],[R2+R4+R6,-(R1+R2),R1+R2+R3+R4+R5+R6,-(R5+R6)],[-R6,0,-(R5+R6),R5+R6+R7]])
#Γράψτε τον πίνακα των σταθερών:
b=n.array([Is,-Vs2,Vs1,-Vs1])
x=n.linalg.solve(A,b)
I1,I2,I3,I4=x[0],x[1],x[2],x[3]
print(“I1= %.5f”%I1) #x[0]=I1
print(“I2= %.5f”%I2) #x[1]=I2
print(“I3= %.5f”%I3) #x[2]=I1
print(“I4= %.5f”%I4) #x[3]=I2
V=R4*(I1+I3)
print("V= %.5f"%V)
Σε αυτό το παράδειγμα, κάθε άγνωστο ρεύμα βρόχου είναι ρεύμα διακλάδωσης (I1, I3 και I4). οπότε είναι εύκολο να ελέγξετε το αποτέλεσμα σε σύγκριση με τα αποτελέσματα ανάλυσης DC του TINA.