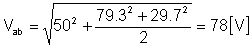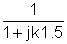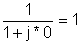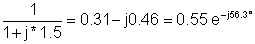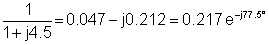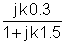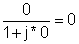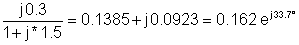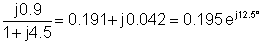Κάντε κλικ ή επιλέξτε τα παρακάτω κυκλώματα Παράδειγμα για να καλέσετε το TINACloud και επιλέξτε τη λειτουργία Interactive DC to Analyze them Online.
Κάντε κλικ ή επιλέξτε τα παρακάτω κυκλώματα Παράδειγμα για να καλέσετε το TINACloud και επιλέξτε τη λειτουργία Interactive DC to Analyze them Online. Πάρτε μια χαμηλού κόστους πρόσβαση στο TINACloud για να επεξεργαστείτε τα παραδείγματα ή να δημιουργήσετε τα δικά σας κυκλώματα
Η Θεώρημα Fourier δηλώνει ότι οποιαδήποτε περιοδική κυματομορφή μπορεί να συντεθεί προσθέτοντας κατάλληλα σταθμισμένους όρους ημιτονοειδούς και συνημίτου διαφόρων συχνοτήτων. Το θεώρημα καλύπτεται καλά σε άλλα εγχειρίδια, οπότε θα συνοψίσουμε μόνο τα αποτελέσματα και θα δείξουμε μερικά παραδείγματα.
Αφήστε την περιοδική συνάρτηση μας να είναι f (t) = f (t ±nT) όπου T είναι ο χρόνος μιας περιόδου και n είναι ακέραιος αριθμός.
w0= 2p/ Τ τη θεμελιώδη γωνιακή συχνότητα.
Με το Θεώρημα Fourier, η περιοδική συνάρτηση μπορεί να γραφτεί ως το ακόλουθο άθροισμα:
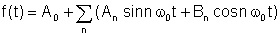
όπου 
An και Βn είναι η Συντελεστές Fourier και το άθροισμα είναι το Σειρά Fourier.
Μια άλλη μορφή, πιθανώς λίγο πιο πρακτική:
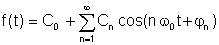
όπου
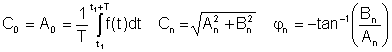
A0 = C0 είναι η DC ή η μέση τιμή, A1, Β1 Και C1 είναι τα βασικά συστατικά, και τα άλλα είναι οι αρμονικοί όροι.
Ενώ μπορεί να απαιτηθούν μόνο μερικοί όροι για την προσέγγιση ορισμένων κυματομορφών, άλλοι θα απαιτούν πολλούς όρους.
Γενικά, όσο περισσότεροι όροι περιλαμβάνονται, τόσο καλύτερη είναι η προσέγγιση, αλλά για κυματομορφές που περιέχουν βήματα, όπως ορθογώνια ερεθίσματα, Φαινόμενο Gibbs μπαίνει στο παιχνίδι. Καθώς ο αριθμός των όρων αυξάνεται, η υπέρβαση συγκεντρώνεται σε μια ολοένα μικρότερη χρονική περίοδο.
An ακόμη και λειτουργία f (t) = f (-t) (συμμετρία άξονα) απαιτεί μόνο όρους συνημίτονο.
An μονή λειτουργία f (t) = - f (-t) (σημείο συμμετρία) απαιτεί μόνο όρους ημιτόνου.
Μια κυματομορφή με συμμετρίας καθρέφτη ή μισού κύματος έχει μόνο περιττός αρμονικές στην αναπαράστασή του Fourier.
Εδώ δεν θα ασχοληθούμε με την επέκταση της σειράς Fourier, αλλά θα χρησιμοποιήσουμε μόνο ένα δεδομένο άθροισμα ημιτονοειδών και συνημίτων ως διέγερση για ένα κύκλωμα.
Στα προηγούμενα κεφάλαια αυτού του βιβλίου, ασχοληθήκαμε με ημιτονοειδή διέγερση. Εάν το κύκλωμα είναι γραμμικό, το θεώρημα υπέρθεσης είναι έγκυρο. Για ένα δίκτυο με μη-ημιτονοειδή περιοδική διέγερση, η υπέρθεση μας επιτρέπει υπολογίστε τα ρεύματα και τις τάσεις που οφείλονται σε κάθε ημιτονοειδή όρο Fourier ένα κάθε φορά. Όταν όλα υπολογίζονται, συνοψίζουμε τελικά τα αρμονικά στοιχεία της απόκρισης.
Είναι λίγο περίπλοκο να προσδιοριστούν οι διαφορετικοί όροι των περιοδικών τάσεων και ρευμάτων και, στην πραγματικότητα, μπορεί να αποφέρει υπερφόρτωση πληροφοριών. Στην πράξη, θα θέλαμε απλώς να κάνουμε μετρήσεις. Μπορούμε να μετρήσουμε τους διαφορετικούς αρμονικούς όρους χρησιμοποιώντας ένα αναλυτής αρμονικών, αναλυτής φάσματος, αναλυτής κυμάτων ή αναλυτής Fourier. Όλα αυτά είναι περίπλοκη και πιθανότατα αποδίδει περισσότερα δεδομένα από ό, τι χρειάζεται. Μερικές φορές αρκεί η περιγραφή ενός περιοδικού σήματος μόνο από τις μέσες τιμές του. Υπάρχουν όμως διάφορα είδη μέσων μετρήσεων.
Μέσος Όρος ΑΞΙΕΣ
Απλός μέσος όρος or DC Ο όρος θεωρήθηκε στην αναπαράσταση Fourier ως Α0
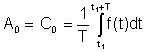
Αυτός ο μέσος όρος μπορεί να μετρηθεί με όργανα όπως το Deprez Όργανα DC.
Αποτελεσματική αξία or rms (root mean square) έχει τον ακόλουθο ορισμό:
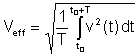
Αυτή είναι η πιο σημαντική μέση τιμή επειδή η θερμότητα που διαχέεται στις αντιστάσεις είναι ανάλογη με την πραγματική τιμή. Πολλά ψηφιακά και ορισμένα αναλογικά βολτόμετρα μπορούν να μετρήσουν την πραγματική τιμή των τάσεων και των ρευμάτων.
Απόλυτος μέσος όρος
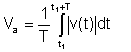
Αυτός ο μέσος όρος δεν είναι πλέον σημαντικός. παλαιότερα όργανα μέτρησαν αυτήν τη μορφή μέσου όρου.
Αν γνωρίζουμε την αναπαράσταση Fourier μιας κυματομορφής τάσης ή ρεύματος, μπορούμε επίσης να υπολογίσουμε τις μέσες τιμές ως εξής:
Απλός μέσος όρος or DC Ο όρος θεωρήθηκε στην αναπαράσταση Fourier ως Α0 = C0
Αποτελεσματική αξία or rms (root mean square) είναι, μετά την ολοκλήρωση της σειράς Fourier της τάσης:
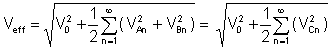
Η παράγοντα klirr είναι μια πολύ σημαντική αναλογία των μέσων τιμών:
Είναι ο λόγος της πραγματικής αξίας των υψηλότερων αρμονικών όρων στην αποτελεσματική αξία της θεμελιώδους αρμονικής:
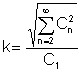

Φαίνεται να υπάρχει αντίφαση εδώ - επιλύουμε το δίκτυο από την άποψη των αρμονικών συστατικών, αλλά μετράμε τις μέσες ποσότητες.
Ας δείξουμε τη μέθοδο με απλά παραδείγματα:
Παράδειγμα 1
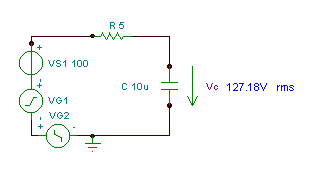
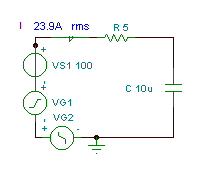
Βρείτε τη συνάρτηση χρόνου και την πραγματική τιμή (rms) της τάσης vC(T)
αν R = 5 ohm, C = 10 mF και v (t) = (100 + 200 cos (w0t) + 30 cos (3 w0t - 90 °)) V, όπου είναι η θεμελιώδης γωνιακή συχνότητα w0= 30 krad / s.
Δοκιμάστε να χρησιμοποιήσετε το θεώρημα υπέρθεσης για να λύσετε το πρόβλημα.
Το πρώτο βήμα είναι να βρείτε τη λειτουργία μεταφοράς ως συνάρτηση της συχνότητας. Για απλότητα, χρησιμοποιήστε την αντικατάσταση: s = j w
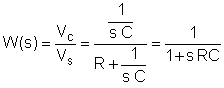
Τώρα αντικαταστήστε τις τιμές των συστατικών και s = jk w0όπου k = 0. 1; 3 σε αυτό το παράδειγμα και w0= 30 krad / s. Σε V, A, ohm, mF και Mrad:
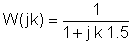
Είναι χρήσιμο να χρησιμοποιήσετε έναν πίνακα για να οργανώσετε τα βήματα της αριθμητικής λύσης:
k | W (jk) = |
0 |
|
1 |
|
3 |
|
Μπορούμε να συνοψίσουμε τα βήματα της λύσης υπέρθεσης σε έναν άλλο πίνακα. Όπως έχουμε ήδη δει, για να βρούμε την πολύπλοκη μέγιστη τιμή ενός στοιχείου, θα πρέπει να πολλαπλασιάσουμε την πολύπλοκη μέγιστη τιμή του στοιχείου της διέγερσης με την τιμή της σύνθετης λειτουργίας μεταφοράς:
k | V | W | VCk |
0 | 100 | 1 | 100 |
1 | 200 | 0.55e-j56.3° | 110e-j56.3° |
3 | 30e-j90° | 0.217e-j77.5° | 6.51e-j167.5° |
Και τέλος μπορούμε να δώσουμε τη συνάρτηση χρόνου γνωρίζοντας τις σύνθετες τιμές αιχμής των στοιχείων:
vC(t) = 100 + 110 cos (w0t - 56.3°) + 6.51 cos (3w0t - 167.5°) V
Η τιμή rms (πραγματική) της τάσης είναι:
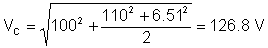
Όπως μπορείτε να δείτε, το όργανο μέτρησης της TINA μετρά αυτή την τιμή rms
Παράδειγμα 2
Βρείτε τη συνάρτηση χρόνου και την πραγματική (rms) τιμή του τρέχοντος i (t)
αν R = 5 ohm, C = 10 mF και v (t) = (100 + 200 cos (w0t) + 30 cos (3w0t - 90 °)) V όπου είναι η θεμελιώδης γωνιακή συχνότητα w0= 30 krad / s.
Προσπαθήστε να λύσετε το πρόβλημα χρησιμοποιώντας το θεώρημα υπέρθεσης.
  |
Τα βήματα της λύσης είναι παρόμοια με το Παράδειγμα 1, αλλά η λειτουργία μεταφοράς είναι διαφορετική.
Τώρα αντικαταστήστε τις αριθμητικές τιμές και s = jk w0,όπου k = 0. 1; 3 σε αυτό το παράδειγμα.
Σε V, A, ohm, mF και Mrad:
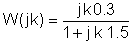
Είναι χρήσιμο να χρησιμοποιείτε έναν πίνακα κατά την αριθμητική λύση:
k | W (jk) = |
0 | |
1 | |
3 | |
Μπορούμε να συνοψίσουμε τα βήματα της υπέρθεσης σε έναν άλλο πίνακα. Όπως έχουμε ήδη δει, για να βρούμε την τιμή αιχμής ενός στοιχείου, θα πρέπει να πολλαπλασιάσουμε την πολύπλοκη μέγιστη τιμή αυτού του στοιχείου της διέγερσης με την τιμή της σύνθετης συνάρτησης μεταφοράς. Χρησιμοποιήστε τις σύνθετες τιμές κορυφής των συστατικών της διέγερσης:
k | VSk | W(jk) | Ik |
0 | 100 | 0 | 0 |
1 | 200 | 0.162 καιj33.7° | 32.4 καιj33.7° |
3 | 30 και-j90° | 0.195 καιj12.5° | 5.85 και-j77.5° |
Και τέλος, γνωρίζοντας τις πολύπλοκες τιμές κορυφής των στοιχείων μπορούμε να δηλώσουμε τη συνάρτηση χρόνου:
i (t) = 32.4 cos (w0t + 33.7°) + 5.85 cos (3w0t - 77.5°) [ΕΝΑ]
Trms τιμή του τρέχοντος:
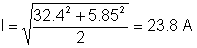
Μπορείτε συχνά να κάνετε έναν έλεγχο λογικής για μέρος της λύσης. Για παράδειγμα, ένας πυκνωτής μπορεί να έχει τάση DC αλλά όχι ρεύμα DC.
Παράδειγμα 3
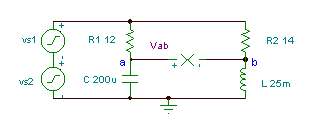
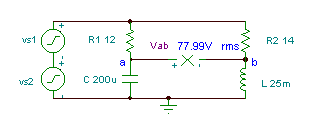
Λάβετε τη συνάρτηση χρόνου της τάσης Vab if R1= 12 ohm, R2 = 14 ohm, L = 25 mH και
C = 200 mF. Η τάση της γεννήτριας είναι v (t) = (50 + 80 cos (w0t) + 30 cos (2 w0t + 60 °)) V, όπου η θεμελιώδης συχνότητα είναι f0 = 50 Hz
Το πρώτο βήμα είναι να βρείτε τη λειτουργία μεταφοράς:
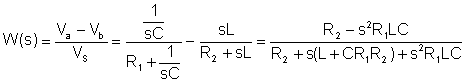
Αντικατάσταση αριθμητικών τιμών σε μονάδες V, A, ohm, mH, mF, kHz:
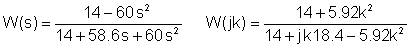
Συγχώνευση των δύο πινάκων:
| k V Sk |   | V abk |
|---|---|---|
| 0 50 |   | 50 |
| 1 80 |   | 79.3 και-j66.3 |
| 2 30 ej60 |   | 29.7 και-j44.7 |
Τέλος η συνάρτηση χρόνου:
vab(t) = 50 + 79.3 cos (w1t - 66.3°) + 29.7 cos (2w1t - 44.7°) [V]
και η τιμή rms: