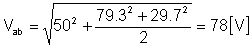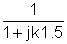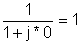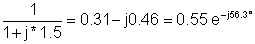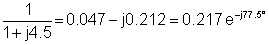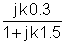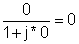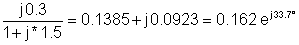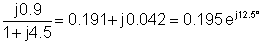Klik atau Ketik litar Contoh di bawah untuk memanggil TINACloud dan pilih mod Interaktif DC untuk Menganalisisnya dalam Talian. Dapatkan akses kos rendah ke TINACloud untuk mengedit contoh atau membuat litar anda sendiri
. Fourier theorem menyatakan bahawa sebarang bentuk gelombang berkala dapat disintesis dengan menambahkan sebutan sinus dan kosinus yang berwajaran tepat dari pelbagai frekuensi. Teorema ini diliputi dengan baik dalam buku teks lain, jadi kami hanya akan meringkaskan hasilnya dan menunjukkan beberapa contoh.
Biarkan fungsi berkala kita menjadi f (t) = f (t ±nT) di mana T adalah masa satu tempoh dan n adalah nombor bulat.
w0= 2p/ T frekuensi sudut asas.
Oleh Fourier theorem, fungsi berkala boleh ditulis sebagai jumlah berikut:
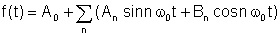
di mana 
An dan Bn adalah Pekali Fourier dan jumlahnya ialah Siri Fourier.
Bentuk lain, mungkin sedikit lebih praktikal:
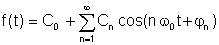
di mana
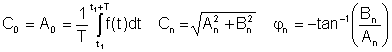
A0 = C0 ialah DC atau nilai purata, A1, B1 dan C1 adalah komponen asas, dan yang lain adalah istilah harmonik.
Walaupun hanya sebilangan istilah yang diperlukan untuk menghampiri beberapa bentuk gelombang, yang lain memerlukan banyak istilah.
Secara amnya, semakin banyak istilah yang disertakan, semakin baik pendekatannya, tetapi untuk bentuk gelombang yang mengandungi langkah, seperti impuls segi empat tepat, Fenomena Gibbs mula bermain. Apabila bilangan istilah meningkat, overshoot menjadi tertumpu dalam jangka masa yang lebih kecil.
An malah berfungsi f (t) = f (-t) (simetri paksi) hanya memerlukan sebutan kosinus.
An fungsi ganjil f (t) = - f (-t) (titik simetri) hanya memerlukan sebutan sinus.
Satu bentuk gelombang dengan cermin atau simetri separuh gelombang hanya mempunyai ganjil harmonik dalam perwakilan Fouriernya.
Di sini kita tidak akan menangani pengembangan siri Fourier, tetapi hanya akan menggunakan sejumlah sinus dan kosinus tertentu sebagai pengujaan untuk rangkaian.
Dalam bab-bab awal buku ini, kita membahas pengujaan sinusoidal. Sekiranya litar linier, maka teorem superposisi ianya sah. Untuk rangkaian dengan pengujaan berkala nonsinusoidal, superposisi membolehkan kita hitung arus dan voltan kerana setiap istilah sinusoid Fourier satu demi satu. Apabila semua dikira, akhirnya kami merangkum komponen harmonik tindak balas.
Agak rumit untuk menentukan pelbagai istilah voltan dan arus berkala dan, sebenarnya, ia mungkin menghasilkan maklumat yang berlebihan. Dalam praktiknya, kami ingin membuat pengukuran. Kita dapat mengukur pelbagai istilah harmonik dengan menggunakan a penganalisis harmonik, penganalisis spektrum, penganalisis gelombang atau penganalisis Fourier. Semua ini adalah rumit dan mungkin menghasilkan lebih banyak data daripada yang diperlukan. Kadang-kadang cukup untuk menggambarkan isyarat berkala hanya dengan nilai purata. Tetapi ada beberapa jenis ukuran purata.
PURATA NILAI-NILAI
Purata mudah or DC istilah dilihat dalam perwakilan Fourier sebagai A0
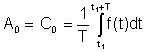
Rata-rata ini dapat diukur dengan instrumen seperti Deprez Instrumen DC.
Nilai berkesan or rms (root mean square) mempunyai definisi berikut:
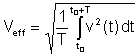
Ini adalah nilai purata yang paling penting kerana haba yang dikeluarkan dalam perintang berkadar dengan nilai efektif. Banyak voltmeter digital dan analog boleh mengukur nilai voltan dan arus berkesan.
Purata mutlak
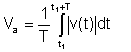
Rata-rata ini tidak lagi penting; instrumen terdahulu mengukur bentuk purata ini.
Sekiranya kita mengetahui perwakilan Fourier bentuk gelombang voltan atau arus, kita juga dapat mengira nilai purata seperti berikut:
Purata mudah or DC istilah dilihat dalam perwakilan Fourier sebagai A0 = C0
Nilai berkesan or rms (root mean square) adalah, setelah mengintegrasikan rangkaian voltan Fourier:
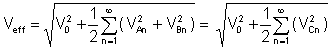
. faktor klirr adalah nisbah nilai purata yang sangat penting:
Ini adalah nisbah nilai efektif bagi istilah harmonik yang lebih tinggi kepada nilai efektif harmonik asas:
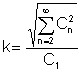
Nampaknya terdapat percanggahan di sini - kami menyelesaikan rangkaian dari segi komponen harmonik, tetapi kami mengukur jumlah purata.
Marilah kita gambarkan kaedah dengan contoh mudah:
1 Contoh
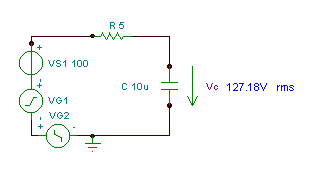
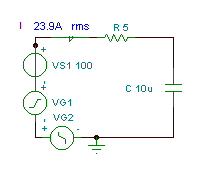
Cari fungsi masa dan nilai efektif (rms) voltan vC(T)
jika R = 5 ohm, C = 10 mF dan v (t) = (100 + 200 cos (w0t) + 30 cos (3 w0t - 90 °)) V, dengan frekuensi sudut asas w0= 30 krad / s.
Cuba gunakan teorema superposisi untuk menyelesaikan masalah.
Langkah pertama adalah mencari fungsi pemindahan sebagai fungsi frekuensi. Untuk kesederhanaan, gunakan pengganti: s = j w
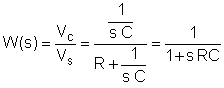
Sekarang ganti nilai komponen dan s = jk w0di mana k = 0; 1; 3 dalam contoh ini dan w0= 30 krad / s. Dalam V, A, ohm, mF dan unit Mrad / s:
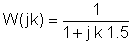
Adalah berguna untuk menggunakan jadual untuk mengatur langkah-langkah penyelesaian berangka:
k | W (jk) = |
0 |
|
1 |
|
3 |
|
Kita dapat meringkaskan langkah penyelesaian superposisi di jadual lain. Seperti yang telah kita lihat, untuk mencari nilai puncak kompleks komponen, kita harus mengalikan nilai puncak kompleks komponen pengujaan dengan nilai fungsi pemindahan kompleks:
k | V | W | VCk |
0 | 100 | 1 | 100 |
1 | 200 | 0.55e-j56.3° | 110e-j56.3° |
3 | 30e-j90° | 0.217e-j77.5° | 6.51e-j167.5° |
Dan akhirnya kita dapat memberi fungsi masa mengetahui nilai puncak komponen yang kompleks:
vC(t) = 100 + 110 cos (w0t - 56.3°) + 6.51 cos (3w0t - 167.5°) V
Nilai rms (berkesan) voltan adalah:
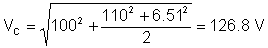
Seperti yang anda lihat, alat ukur TINA mengukur nilai rms ini.
2 Contoh
Cari fungsi masa dan nilai efektif (rms) semasa (t)
jika R = 5 ohm, C = 10 mF dan v (t) = (100 + 200 cos (w0t) + 30 cos (3w0t - 90 °)) V dengan frekuensi sudut asas w0= 30 krad / s.
Cuba selesaikan masalah menggunakan teorem superposisi.
 |
Langkah penyelesaiannya serupa dengan Contoh 1, tetapi fungsi pemindahannya berbeza.
Sekarang gantikan nilai berangka dan s = jk w0,di mana k = 0; 1; 3 dalam contoh ini.
Dalam V, A, ohm, mF dan unit Mrad / s:
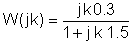
Sangat berguna untuk menggunakan jadual semasa penyelesaian berangka:
k | W (jk) = |
0 | |
1 | |
3 | |
Kita dapat meringkaskan langkah-langkah superposisi di jadual lain. Seperti yang telah kita lihat, untuk mencari nilai puncak komponen, kita harus mengalikan nilai puncak kompleks komponen pengujaan dengan nilai fungsi pemindahan kompleks. Gunakan nilai puncak kompleks komponen pengujaan:
k | VSk | W(jk) | Ik |
0 | 100 | 0 | 0 |
1 | 200 | 0.162 danj33.7° | 32.4 danj33.7° |
3 | 30 dan-j90° | 0.195 danj12.5° | 5.85 dan-j77.5° |
Dan akhirnya, dengan mengetahui nilai puncak komponen yang kompleks, kita dapat menyatakan fungsi masa:
i (t) = 32.4 cos (w0t + 33.7°) + 5.85 cos (3w0t - 77.5°) [A]
Tdia nilai semasa:
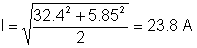
Anda sering boleh melakukan pemeriksaan kewarasan untuk sebahagian penyelesaiannya. Contohnya, kapasitor boleh mempunyai voltan DC tetapi bukan arus DC.
3 Contoh
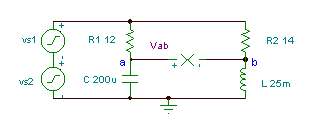
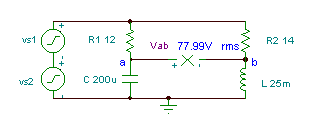
Dapatkan fungsi masa voltan Vab if R1= 12 ohm, R2 = 14 ohm, L = 25 mH, dan
C = 200 mF. Voltan penjana adalah v (t) = (50 + 80 cos (w0t) + 30 cos (2 w0t + 60 °)) V, di mana frekuensi asas adalah f0 = 50 Hz.
Langkah pertama adalah mencari fungsi pemindahan:
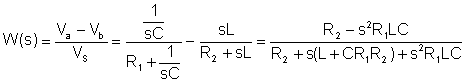
Menggantikan nilai berangka dalam unit V, A, ohm, mH, mF, kHz:
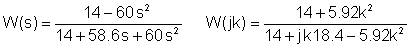
Menggabungkan dua jadual:
| k V Sk |  | V abk |
|---|---|---|
| 0 50 |  | 50 |
| 1 80 |  | 79.3 dan-j66.3 |
| 2 30 ej60 |  | 29.7 dan-j44.7 |
Akhirnya fungsi masa:
vab(t) = 50 + 79.3 cos (w1t - 66.3°) + 29.7 cos (2w1t - 44.7°) [V]
dan nilai rms:
English
English
German
French
Spanish
Portuguese
Russian
Chinese (Simplified)
Chinese (Traditional)
Japanese
Korean
Hungarian