9. FET Amplifier analysis

CURRENT – 9. FET Amplifier analysis

PREVIOUS- 8. FET Amplifiers – Canonical configurations

NEXT- 10. FET Amplifier design

FET Amplifier analysis

9.1 The CS (and Source Resistor) Amplifier

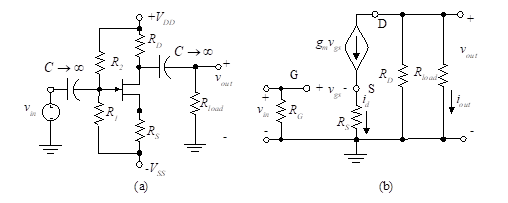
Figure 33 – The CS amplifier with source resistor

Figure 33(a) shows the CS amplifier with source resistor. The ac equivalent circuit is in Figure 33(b). We assume r_o is large compared to , so it can be neglected. If a capacitor is present between source and ground (i.e., the CS amplifier), we need simply set R_S equal to zero in the following ac equations. We do this at the conclusion of this derivation.

In part (b) of Figure 33, R_G is the parallel combination of R₁ and R₂ and V_GG is the Thevenin equivalent voltage of the bias circuit:

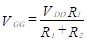 (41)

To analyze the ac equivalent circuit, we write a KVL equation around the gate circuit.

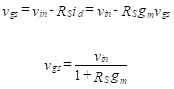 (42)

The output voltage, v_out, is given by

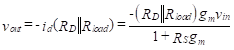
The voltage gain, A_v, is now found.

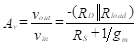 (43)

If the source resistance, R_S, is bypassed by a capacitor, we let R_S = 0, and the voltage gain increases to

 (44)

This is typically a large negative number.

The input resistance and current gain are given by

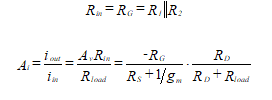 (45)

9.2 The CG Amplifier

Figure 37(a) shows the single-stage common-gate amplifier and Figure 6.37(b) shows its ac equivalent. We have once again neglected r_o under the assumption that it is large compared to the parallel combination of R_D with R_load.

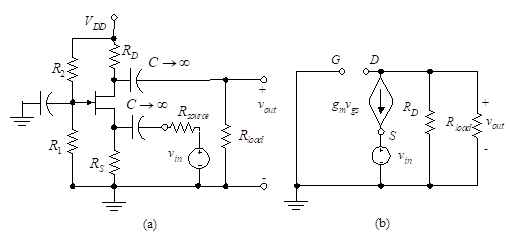
Figure 37 – CG amplifier

From Figure 37(b) leftmost loop, the gate-to-source voltage is given by

 (46)

The current through R_S is

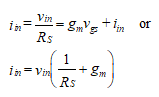 (47)

so the (input) resistance seen by the source is

 (48)

This should be compared to Equation (45) for the CS amplifier. We see that if the gate resistance is high, the input resistance of the common-source amplifier can be much larger than that of the common-gate amplifier. In fact, the number of applications of the CG amplifier is limited due to the low input impedance.

The voltage gain is given by

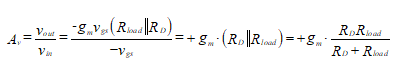 (49)

Comparing this with Equation (44) , we see that the voltage gain for the CS amplifier with an unbypassed resistance in the source circuit is the same as that of the CG amplifier except the CG amplifier does not shift the phase.

The output resistance is simply given by R_D (put in a test current and measure the voltage while setting v_in to zero).

The current gain of the CG amplifier is

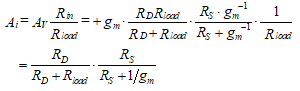 (50)

9.3 The CD (SF) Amplifier

Figure 39(a) shows the single-stage common-drain source follower (SF) amplifier and Figure 39(b) shows its ac equivalent. As with each configuration we have analyzed, we omit the large resistance, r_o under the assumption it is much larger than the parallel combination of R_S with R_load.

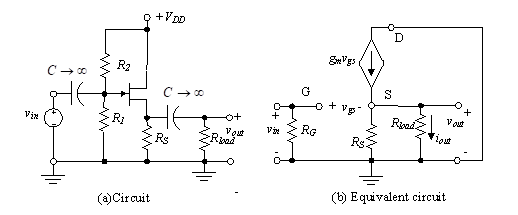
Figure 39 – The CD amplifier

The input resistance is simply R_in = R_G. Writing a KVL equation around the gate-to-source loop, we have

 (51)

from which we obtain

 (52)

The output voltage is

 (53)

The voltage gain is the ratio of output to input voltage.

 (54)

Note that this voltage gain is less than unity, and it approaches one as the parallel combination of R_S with R_load increases.

We now find the current gain. The output current is the ratio of the output voltage to the load resistance. The input current is the input voltage divided by R_G. The gain is therefore given by

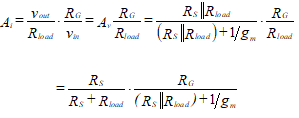 (55)

The output resistance can be found by replacing the load resistor with a test voltage, v_test, and then finding the resulting current, i_test. The current driven by this test source is found from a node equation at the source.

 (56)

The gate-to-source voltage is simply -v_test since we assume the input voltage is zero. Therefore, the output resistance is

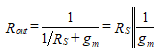 (57)

PREVIOUS- 8. FET Amplifiers – Canonical configurations

NEXT- 10. FET Amplifier design