Klikk eller trykk på Eksempel kretsene nedenfor for å påkalle TINACloud og velg Interaktiv DC-modus for å analysere dem på nettet.
Klikk eller trykk på Eksempel kretsene nedenfor for å påkalle TINACloud og velg Interaktiv DC-modus for å analysere dem på nettet. Få billig tilgang til TINACloud for å redigere eksemplene eller opprette dine egne kretser
Som vi allerede har sett, kan kretsløp med sinusformet eksitering løses ved hjelp av komplekse impedanser for elementene og kompleks topp or komplekse rms verdier for strøm og spenning. Ved hjelp av versjonen av komplekse verdier av Kirchhoffs lover kan nodal- og mesh-analyseteknikker brukes til å løse vekselstrømskretser på en måte som ligner på likestrømskretser. I dette kapittelet vil vi vise dette gjennom eksempler på Kirchhoffs lover.
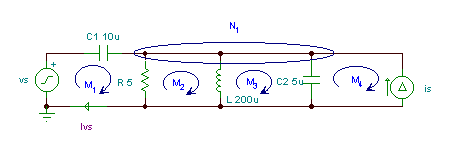
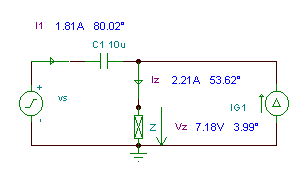
Eksempel 1
Finn amplituden og fasevinkelen til strømmen ivs(T) if
vS(t) = VSM cos 2pft; jeg (t) = ISM cos 2pft; VSM = 10 V; JegSM = 1 A; f = 10 kHz;
Til sammen har vi 10 ukjente spenninger og strømmer, nemlig: i, iC1, TheR, TheL, TheC2iC1iRiLiC2 og vIS. (Hvis vi bruker komplekse topp- eller rms-verdier for spenninger og strømmer, har vi til sammen 20 reelle ligninger!)
Ligningene:
Loop eller mesh ligninger: for M1 - VSM +VC1M+VRM = 0
M2 - VRM + VLM = 0
M3 - VLM + VC2M = 0
M4 - VC2M + VEr m = 0
Ohms lover VRM = R *IRM
VLM = j*w* L *ILM
IC1M = j*w*C1*VC1M
IC2M = j*w*C2*VC2M
Nodal ligning for N1 - IC1M - ISM + IRM + ILM +IC2M = 0
for serieelementer I = IC1MLøsning av ligningssystemet kan du finne den ukjente strømmen:
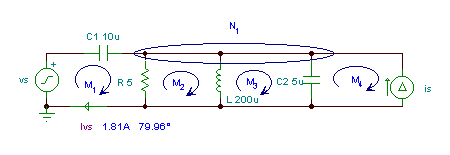
ivs (t) = 1.81 cos (wt + 79.96°) A
Å løse et så stort system med komplekse ligninger er veldig komplisert, så vi har ikke vist det i detalj. Hver komplekse ligning fører til to reelle ligninger, så vi viser løsningen bare ved verdiene beregnet med TINAs tolk.
Løsningen ved hjelp av TINAs tolk:
OM: = 20000 * pi;
Vs: = 10;
Er: = 1;
Sys Ic1, Ir, IL, Ic2, Vc1, Vr, VL, Vc2, Vis, Ivs
Vs=Vc1+Vr {M1}
Vr=VL {M2}
Vr=Vc2 {M3}
Vc2=Vis {M4}
Ivs=Ir+IL+Ic2-Is {N1}
{Ohms regler}
Ic1 = j * om * C1 * Vc1
Vr = R * Ir
VL = j * om * L * IL
Ic2 = j * om * C2 * Vc2
IVs = Ic1
ende;
IVS = [3.1531E1 + 1.7812E0 * j]
abs (IVS) = [1.8089]
fiIvs: = 180 * bue (IVS) / pi
fiIvs = [79.9613]
import sympy som s
importer cmath som c
cp= lambda Z : "{:.4f}".format(Z)
om=20000 XNUMX*c.pi
Vs=10
Er=1
Ic1,Ir,IL,Ic2,Vc1,Vr,VL,Vc2,Vis,Ivs=s.symbols('Ic1 Ir IL Ic2 Vc1 Vr VL Vc2 Vis Ivs')
A=[s.Eq(Vc1+Vr,Vs),s.Eq(VL,Vr),s.Eq(Vc2,Vr),s.Eq(Vis,Vc2), #M1, M2, M3, M4
s.Eq(Ir+IL+Ic2-Is,Ivs), #N1
s.Eq(1j*om*C1*Vc1,Ic1),s.Eq(R*Ir,Vr),s.Eq(1j*om*L*IL,VL),s.Eq(1j*om*C2*Vc2,Ic2),s.Eq(Ic1,Ivs)] #Ohm’s rules
Ic1,Ir,IL,Ic2,Vc1,Vr,VL,Vc2,Vis,Ivs=[complex(Z) for Z in tuple(s.linsolve(A,(Ic1,Ir,IL,Ic2,Vc1,Vr,VL,Vc2,Vis,Ivs)))[0]]
print (ivs)
print(“abs(Ivs)=”,cp(abs(Ivs)))
print(“180*c.phase(Ivs)/c.pi=”,cp(180*c.phase(Ivs)/c.pi))
Løsningen ved bruk av TINA:
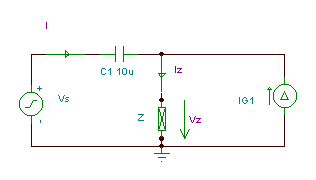
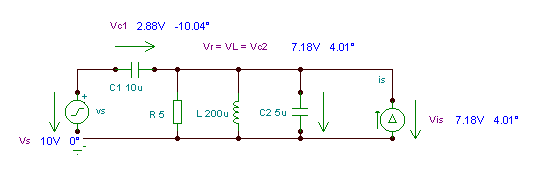
For å løse dette problemet for hånd, arbeid med de komplekse impedansene. For eksempel R, L og C2 er koblet parallelt, slik at du kan forenkle kretsen ved å beregne deres parallelle ekvivalenter. || betyr parallellekvivalent av impedansene:
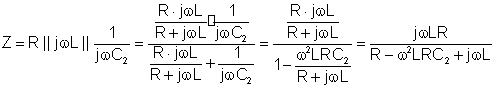
Numerisk:
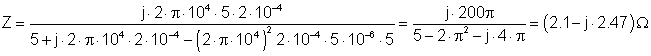
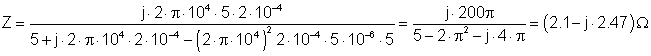
Den forenklede kretsen som bruker impedansen:
Ligningene i ordnet form: I + IG1 = IZ
VS = VC1 +VZ
VZ = Z · IZ
I = j w C1· VC1
Det er fire ukjente- I; IZ; VC1; VZ - og vi har fire ligninger, så en løsning er mulig.
Uttrykke I etter å ha erstattet de andre ukjente fra ligningene:
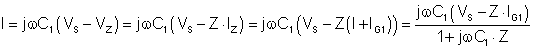
Numerisk
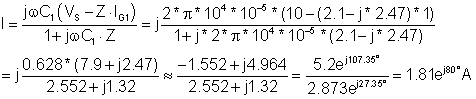
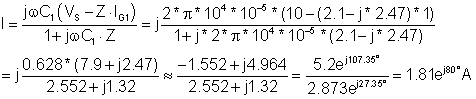
I følge TINAs tolkes resultat.
OM: = 20000 * pi;
Vs: = 10;
Er: = 1;
Z: = replus (R, replus (j * om * L, 1 / j / om / C2));
Z = [2.1046E0-2.4685E0 * j]
sys jeg
I = j * om * C1 * (Vs-Z * (I + Is))
ende;
I = [3.1531E1 + 1.7812E0 * j]
abs (I) = [1.8089]
180 * bue (I) / pi = [79.9613]
import sympy som s
importer cmath som c
Replus= lambda R1, R2 : R1*R2/(R1+R2)
om=20000 XNUMX*c.pi
Vs=10
Er=1
Z=Replus(R,Replus(1j*om*L,1/1j/om/C2))
print('Z=',cp(Z))
I=s.symbols('I')
A=[s.Eq(1j*om*C1*(Vs-Z*(I+Is)),I),]
I=[kompleks(Z) for Z i tuppel(s.linsolve(A,I))[0]][0]
print(“I=”,cp(I))
print(“abs(I)=”,cp(abs(I)))
print(“180*c.fase(I)/c.pi=”,cp(180*c.fase(I)/c.pi))
Tidsfunksjonen til strømmen er da:
I (t) = 1.81 cos (wt + 80°) A
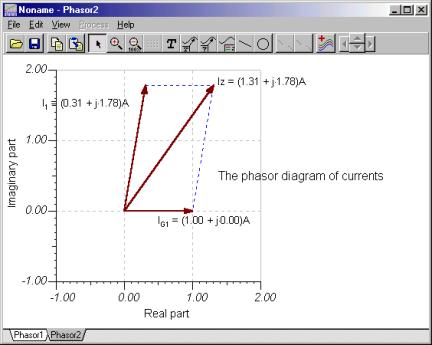
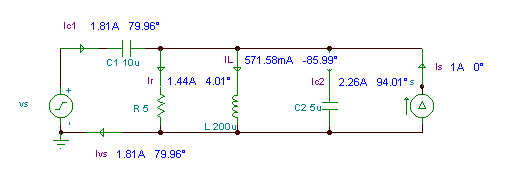
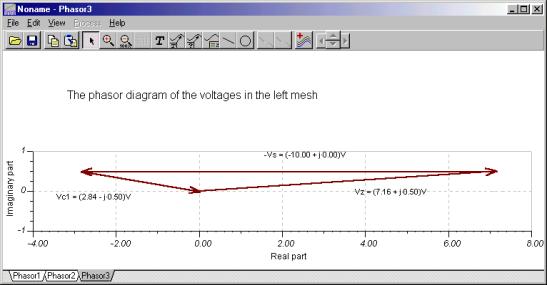
Du kan sjekke Kirchhoffs gjeldende regel ved hjelp av fasediagrammer. Bildet nedenfor ble utviklet ved å sjekke nodeligningen i iZ = jeg + jegG1 danne. Det første diagrammet viser fasorene lagt til ved parallellogramregel, det andre illustrerer trekantregelen for fasortilsetningen.
La oss nå demonstrere KVR ved hjelp av TINAs fasediagramfunksjon. Siden kildespenningen er negativ i ligningen, koblet vi voltmeteret "bakover". Fasordiagrammet illustrerer den opprinnelige formen for Kirchhoffs spenningsregel.
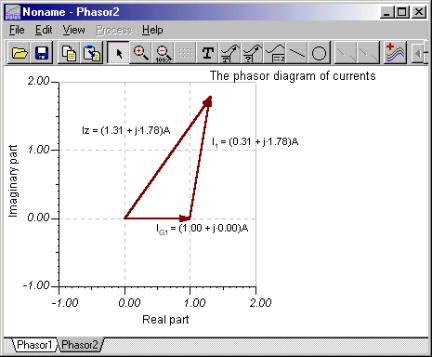
Det første fasordiagrammet bruker parallellogramregelen, mens det andre bruker trekantregelen.
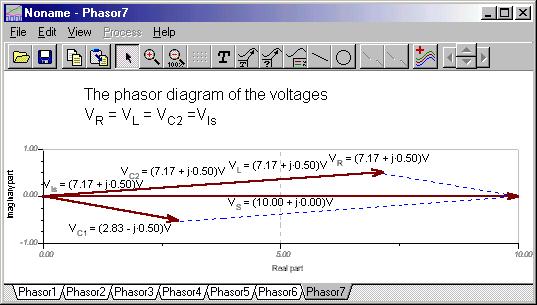
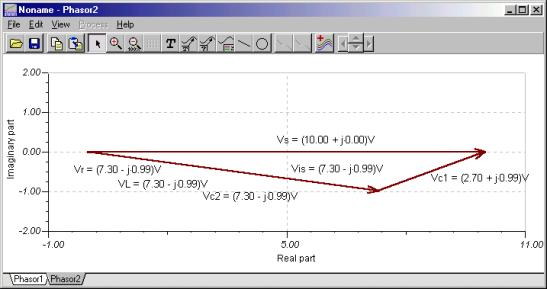
For å illustrere KVR i form VC1 + VZ - VS = 0, vi koblet igjen voltmeteret til spenningskilden bakover. Du kan se at fasordrianten er lukket.
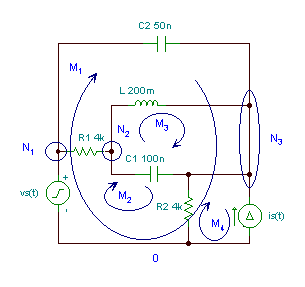
Eksempel 2
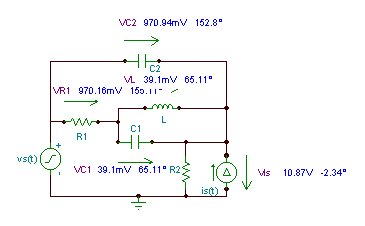
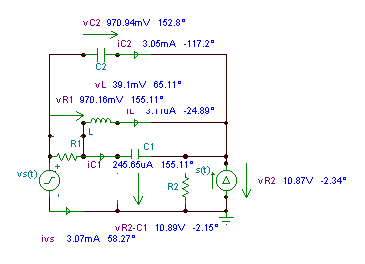
Finn spenningene og strømningene til alle komponentene hvis:
vS(t) = 10 cos wTV, iS(t) = 5 cos (w t + 30 °) mA;
C1 = 100 nF, C2 = 50 nF, R1 = R2 = 4 k; L = 0.2 H, f = 10 kHz.
La de ukjente være de komplekse toppverdiene til spenningene og strømmen til 'passive' elementer, så vel som strømmen til spenningskilden (iVS ) og spenningen til strømkilden (vIS ). Til sammen er det tolv sammensatte ukjente. Vi har tre uavhengige noder, fire uavhengige løkker (merket som MI), og fem passive elementer som kan karakteriseres av fem “Ohms lover” - til sammen er det 3 + 4 + 5 = 12 ligninger:
Nodal ligninger for N1 IVSM = IR1M + IC2M
for N2 IR1M = ILM + IC1M
for N3 IC2M + ILM + IC1M +IsM = IR2M
Loop-ligninger for M1 VSM = VC2M + VR2M
for M2 VSM = VC1M + VR1M+ VR2M
for M3 VLM = VC1M
for M4 VR2M = VEr m
Ohms lover VR1M = R1*IR1M
VR2M = R2*IR2M
IC1m = j *w*C1*VC1M
IC2m = j *w*C2*VC2M
VLM = j *w* L * ILM
Ikke glem at en hvilken som helst kompleks ligning kan føre til to reelle ligninger, så Kirchhoffs metode krever mange beregninger. Det er mye enklere å løse tidsfunksjonene til spenninger og strømmer ved hjelp av et system med differensiallikninger (ikke diskutert her). Først viser vi resultatene beregnet av TINAs tolk:
f: = 10000;
Vs: = 10;
s: = 0.005 * exp (j * pi / 6);
om: = 2 * pi * f;
sys ir1, ir2, ic1, ic2, iL, vr1, vr2, vc1, vc2, vL, vis, ivs
ivs=ir1+ic2 {1}
ir1=iL+ic1 {2}
ic2+iL+ic1+Is=ir2 {3}
Vs=vc2+vr2 {4}
Vs=vr1+vr2+vc1 {5}
vc1=vL {6}
vr2=vis {7}
vr1=ir1*R1 {8}
vr2=ir2*R2 {9}
ic1=j*om*C1*vc1 {10}
ic2=j*om*C2*vc2 {11}
vL=j*om*L*iL {12}
ende;
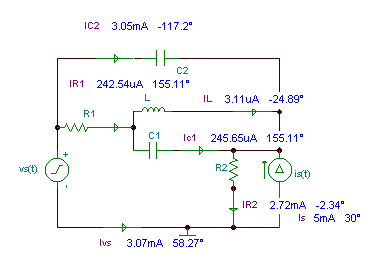
abs (vr1) = [970.1563m]
abs (vr2) = [10.8726]
abs (ic1) = [245.6503u]
abs (ic2) = [3.0503m]
abs (vc1) = [39.0965m]
abs (vc2) = [970.9437m]
abs (iL) = [3.1112u]
abs (VI) = [39.0965m]
abs (IVS) = [3.0697m]
180 + radtodeg (ARC (IVS)) = [58.2734]
abs (vis) = [10.8726]
radtodeg (arc (vis)) = [- 2.3393]
radtodeg (arc (vr1)) = [155.1092]
radtodeg (arc (vr2)) = [- 2.3393]
radtodeg (arc (ic1)) = [155.1092]
radtodeg (arc (ic2)) = [- 117.1985]
radtodeg (arc (vc2)) = [152.8015]
radtodeg (arc (vc1)) = [65.1092]
radtodeg (arc (iL)) = [- 24.8908]
radtodeg (arc (VI)) = [65.1092]
import sympy som s
importere matematikk som m
importer cmath som c
cp= lambda Z : "{:.4f}".format(Z)
f = 10000
Vs=10
S=0.005*c.exp(1j*c.pi/6)
om=2*c.pi*f
ir1,ir2,ic1,ic2,iL,vr1,vr2,vc1,vc2,vL,vis,ivs=s.symbols('ir1 ir2 ic1 ic2 iL vr1 vr2 vc1 vc2 vL vis ivs')
A=[s.Eq(ir1+ic2,ivs), #1
s.Eq(iL+ic1,ir1), #2
s.Eq(ic2+iL+ic1+Is,ir2), #3
s.Eq(vc2+vr2,Vs), #4
s.Eq(vr1+vr2+vc1,Vs), #5
s.Eq(vL,vc1), #6
s.Eq(vis,vr2), #7
s.Eq(ir1*R1,vr1), #8
s.Eq(ir2*R2,vr2), #9
s.Eq(1j*om*C1*vc1,ic1), #10
s.Eq(1j*om*C2*vc2,ic2), #11
s.Eq(1j*om*L*iL,vL)] #12
ir1,ir2,ic1,ic2,iL,vr1,vr2,vc1,vc2,vL,vis,ivs=[complex(Z) for Z in tuple(s.linsolve(A,(ir1,ir2,ic1,ic2,iL,vr1,vr2,vc1,vc2,vL,vis,ivs)))[0]]
print(“abs(vr1)=”,cp(abs(vr1)))
print(“abs(vr2)=”,cp(abs(vr2)))
print(“abs(ic1)=”,cp(abs(ic1)))
print(“abs(ic2)=”,cp(abs(ic2)))
print(“abs(vc1)=”,cp(abs(vc1)))
print(“abs(vc2)=”,cp(abs(vc2)))
print(“abs(iL)=”,cp(abs(iL)))
print(“abs(vL)=”,cp(abs(vL)))
print(“abs(ivs)=”,cp(abs(ivs)))
print(“180+degrees(phase(ivs))=”,cp(180+m.degrees(c.phase(ivs))))
print(“abs(vis)=”,cp(abs(vis)))
print(“degrees(phase(vis))=”,cp(m.degrees(c.phase(vis))))
print(“degrees(phase(vr1))=”,cp(m.degrees(c.phase(vr1))))
print(“degrees(phase(vr2))=”,cp(m.degrees(c.phase(vr2))))
print(“degrees(phase(ic1))=”,cp(m.degrees(c.phase(ic1))))
print(“degrees(phase(ic2))=”,cp(m.degrees(c.phase(ic2))))
print(“degrees(phase(vc2))=”,cp(m.degrees(c.phase(vc2))))
print(“degrees(phase(vc1))=”,cp(m.degrees(c.phase(vc1))))
print(“degrees(phase(iL))=”,cp(m.degrees(c.phase(iL))))
print(“degrees(phase(vL))=”,cp(m.degrees(c.phase(vL))))
Prøv nå å forenkle likningene for hånd ved å bruke substitusjon. Første erstatter ekv.9. til ekvivalent 5.
VS = VC2 + R2 IR2 en.)
deretter eq.8 og eq.9. inn i eq 5.
VS = VC1 + R2 IR2 + R1 IR1 b.)
deretter eq 12., eq. 10. og jegL fra eq. 2 til eq.6.
VC1 = VL = jwLIL = jwL (jegR1 - JEGC1) = jwLIR1 - jwL jwC1 VC1
Express VC1
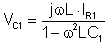
Express VC2 fra ekv. 4. og ekv. og erstatter ekv. 5, ekv. 8. og VC1:
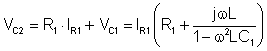
Sett inn ekv. 2., 10., 11. og d.) I ekv.3. og uttrykker jegR2
IR2 = IC2 + IR1 + IS = jwC2 VC2 + IR1 + IS
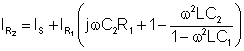
Erstatt nå d.) Og e.) I ekv. 4 og uttrykk jegR1
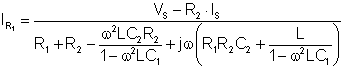
Numerisk:
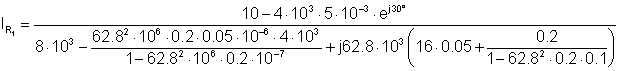
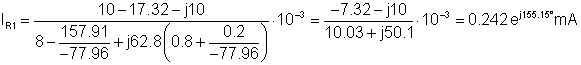
Tidsfunksjonen til iR1 er følgende:
iR1(t) = 0.242 cos (wt + 155.5°) mA
Målte spenninger: