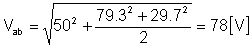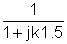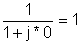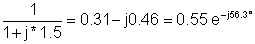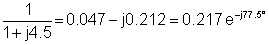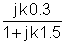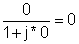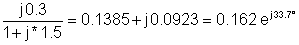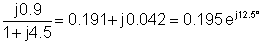Klikk eller trykk på Eksempel kretsene nedenfor for å påkalle TINACloud og velg Interaktiv DC-modus for å analysere dem på nettet.
Få billig tilgang til TINACloud for å redigere eksemplene eller opprette dine egne kretser

De Fourier-setningen angir at enhver periodisk bølgeform kan syntetiseres ved å legge passende vektede sinus- og kosinusbegrep for forskjellige frekvenser. Teoremet er godt dekket i andre lærebøker, så vi vil bare oppsummere resultatene og vise noen eksempler.

La vår periodiske funksjon være f (t) = f (t ±nT) hvor T er tiden for en periode og n er et heltall.

w₀= 2p/ T den grunnleggende kantfrekvensen.

Av den Fourier teorem, den periodiske funksjonen kan skrives som følgende sum:

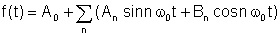
hvor

A_n og b_n er Fourier-koeffisienter og summen er Fourier-serien.

En annen form, sannsynligvis litt mer praktisk:

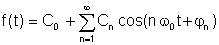
hvor

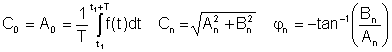
A₀ = C₀ er DC eller gjennomsnittsverdi, A₁, B₁ og C₁ er de grunnleggende komponentene, og de andre er de harmoniske begrepene.

Selv om bare noen få termer kan være nødvendige for å tilnærme noen bølgeformer, vil andre kreve mange vilkår.

Generelt, jo flere begreper inkludert, jo bedre er tilnærmingen, men for bølgeformer som inneholder trinn, for eksempel rektangulære impulser, Gibbs fenomen kommer inn i spillet. Når antallet begreper øker, blir overskuddet konsentrert i en stadig mindre periode.

An selv funksjon f (t) = f (-t) (aksesymmetri) krever bare kosinusbegrep.

An merkelig funksjon f (t) = - f (-t) (punktsymmetri) krever bare sine termer.

En bølgeform med speil eller halvbølge symmetri har bare Odd harmoniske i sin Fourier-representasjon.

Her vil vi ikke takle Fourier-serien utvidelse, men bare bruke en gitt sum av sines og kosinus som en eksitasjon for en krets.

I de tidligere kapitlene i denne boken behandlet vi sinusoidal eksitasjon. Hvis kretsen er lineær, vil superposisjonsteorem er gyldig. For et nettverk med nonsinusoidal periodisk eksitasjon, lar superposisjon oss gjøre det beregne strømmer og spenninger på grunn av hver Fourier sinusform en om gangen. Når alt er beregnet, oppsummerer vi til slutt de harmoniske komponentene i responsen.

Det er litt komplisert å bestemme de forskjellige vilkårene for periodiske spenninger og strømmer, og faktisk kan det gi en overbelastning av informasjon. I praksis vil vi bare gjøre målinger. Vi kan måle de forskjellige harmoniske begrepene ved å bruke a harmonisk analysator, spektrumanalysator, bølgeanalysator eller Fourier-analysator. Alle disse er komplisert og gir sannsynligvis mer data enn nødvendig. Noen ganger er det tilstrekkelig å beskrive et periodisk signal bare med dets gjennomsnittsverdier. Men det er flere typer gjennomsnittlige målinger.

GJENNOMSNITT VERDIER

Enkelt gjennomsnitt or DC begrep ble sett i Fourier-representasjonen som A₀

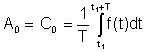
Dette gjennomsnittet kan måles med instrumenter som Deprez DC-instrumenter.

Effektiv verdi or rms (root mean square) har følgende definisjon:

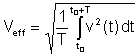
Dette er den viktigste gjennomsnittsverdien fordi varmen som avledes i motstander er proporsjonal med den effektive verdien. Mange digitale og noen analoge voltmetre kan måle effektiv verdi på spenninger og strømmer.

Absolutt gjennomsnitt

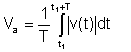
Dette gjennomsnittet er ikke lenger viktig; tidligere instrumenter målte denne formen for gjennomsnittet.

Hvis vi kjenner Fourier-representasjonen av en spennings- eller strømbølgeform, kan vi også beregne gjennomsnittsverdiene som følger:

Enkelt gjennomsnitt or DC begrep ble sett i Fourier-representasjonen som A₀ = C₀

Effektiv verdi or rms (root mean square) er etter integrering av Fourier-serien av spenningen:

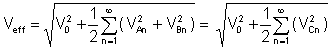
De klirr-faktor er et veldig viktig forhold mellom gjennomsnittsverdiene:

Det er forholdet mellom den effektive verdien av de høyere harmoniske begrepene til den effektive verdien av den grunnleggende harmonikken:

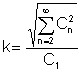
Det ser ut til å være en motsetning her - vi løser nettverk når det gjelder harmoniske komponenter, men vi måler gjennomsnittsmengder.

La oss illustrere metoden ved enkle eksempler:

Eksempel 1

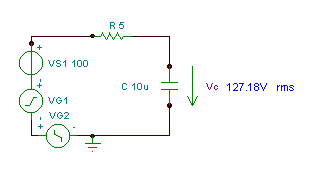
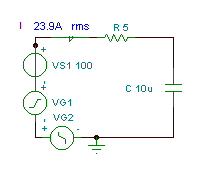
Finn tidsfunksjonen og den effektive (rms) verdien til spenningen v_C(T)

Prøv å bruke superposisjonsteoremet for å løse problemet.

Det første trinnet er å finne overføringsfunksjonen som en funksjon av frekvensen. For enkelhets skyld bruker du substitusjonen: s = j w

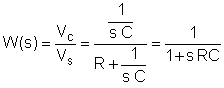
Erstatt nå komponentverdiene og s = jk w₀hvor k = 0; 1; 3 i dette eksemplet og w₀= 30 krad / s. I V, A, ohm, mF og Mrad / s enheter:

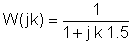
Det er nyttig å bruke en tabell for å organisere trinnene i den numeriske løsningen:

Vi kan oppsummere trinnene i superposisjonsløsningen i en annen tabell. Som vi allerede har sett, bør vi multiplisere den komplekse toppverdien for komponenten til eksitasjonen med verdien av den komplekse overføringsfunksjonen for å finne den komplekse toppverdien til en komponent:

Og til slutt kan vi gi tidsfunksjonen ved å kjenne til de komplekse toppverdiene for komponentene:

v_C(t) = 100 + 110 cos (w₀t - 56.3°) + 6.51 cos (3w₀t - 167.5°) V

Rms (effektive) verdien til spenningen er:

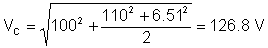
Som du kan se, måler TINA måleinstrument denne rms-verdien.

Eksempel 2

Finn tidsfunksjonen og den effektive (rms) verdien til gjeldende i (t)

Forsøk å løse problemet ved å bruke superposisjonen.

Erstatt nå de numeriske verdiene og s = jk w_0,hvor k = 0; 1; 3 i dette eksemplet.

I V, A, ohm, mF og Mrad / s enheter:

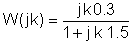
Det er nyttig å bruke en tabell under den numeriske løsningen:

Vi kan oppsummere trinnene i superposisjonen i en annen tabell. Som vi allerede har sett, for å finne toppverdien til en komponent, bør vi multiplisere den komplekse toppverdien til den komponenten i eksitasjonen med verdien av den komplekse overføringsfunksjonen. Bruk de komplekse toppverdiene for komponentene i eksitasjonen:

Og til slutt, når vi kjenner til de komplekse toppverdiene for komponentene, kan vi oppgi tidsfunksjonen:

I (t) = 32.4 cos (w₀t + 33.7°) + 5.85 cos (3w₀t - 77.5°) [EN]

Than rms verdien av strømmen:

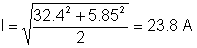
Du kan ofte gjøre en tilregnelighetskontroll for en del av løsningen. For eksempel kan en kondensator ha likespenning, men ikke likestrøm.

Eksempel 3

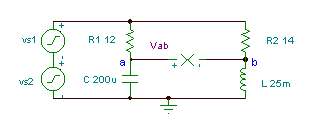
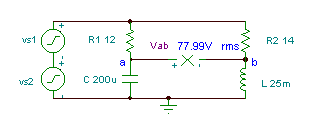
Få tidsfunksjonen til spenningen V_ab if R₁= 12 ohm, R₂ = 14 ohm, L = 25 mH, og

Det første trinnet er å finne overføringsfunksjonen:

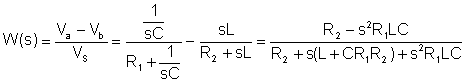
Ved å erstatte numeriske verdier i V, A, ohm, mH, mF, kHz enheter:

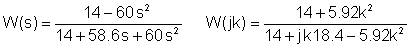
Slå sammen de to tabellene:

k V Sk		V ABK
0		50
1		79.3 og-j66.3
2 30 ej60		29.7 og-j44.7

v_ab(t) = 50 + 79.3 cos (w₁t - 66.3°) + 29.7 cos (2w₁t - 44.7°) [V]

og rms-verdien: