Klikk eller trykk på Eksempel kretsene nedenfor for å påkalle TINACloud og velg Interaktiv DC-modus for å analysere dem på nettet.
Klikk eller trykk på Eksempel kretsene nedenfor for å påkalle TINACloud og velg Interaktiv DC-modus for å analysere dem på nettet. Få billig tilgang til TINACloud for å redigere eksemplene eller opprette dine egne kretser
En sinusformet spenning kan beskrives ved ligningen:
v (t) = VM synd (ωt + Φ) eller v (t) = VM cos (ωt + Φ)
| hvor | v (t) | Øyeblikkelig verdi av spenningen, i volt (V). |
| VM | Maksimal eller toppverdien av spenningen, i volt (V) | |
| T | Periode: Tiden tatt for en syklus, i sekunder | |
| f | Frekvens - antall perioder i 1 andre, i Hz (Hertz) eller 1 / s. f = 1 / T | |
| ω | Vinkelfrekvens, uttrykt i radianer / s ω = 2 * π * f eller ω = 2 * π / T. | |
| Φ | Første fase gitt i radianer eller grader. Denne mengden bestemmer verdien av sinus- eller cosinusbølgen til = 0. | |
| Merk: Amplituden til en sinusformet spenning er noen ganger uttrykt som Veff, den effektive eller RMS-verdien. Dette er relatert til VM i henhold til forholdet VM= √2Veff, eller omtrent Veff = 0.707 VM |
Her er noen eksempler for å illustrere vilkårene ovenfor.
Egenskapene til 220 V vekselstrøm i husholdningssteder i Europa:
Effektiv verdi: Veff = 220 V
Peak verdi: VM= √2 * 220 V = 311 V
Frekvens: f = 50 1 / s = 50 Hz
Vinkelfrekvens: ω = 2 * π * f = 314 1 / s = 314 rad / s
Periode: T = 1 / f = 20 ms
Tidsfunksjon: v (t) = 311 sin (314 t)
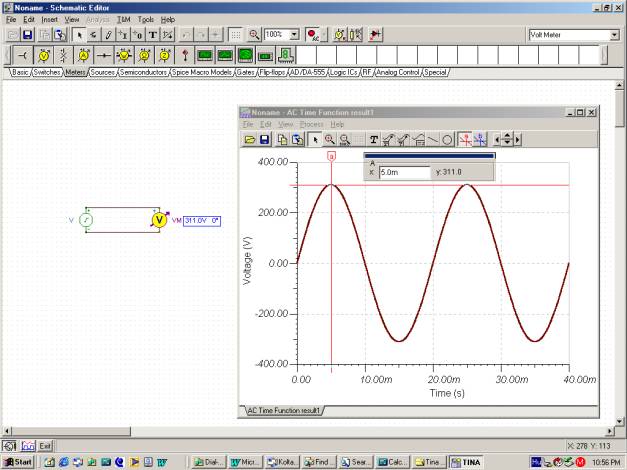
La oss se tidsfunksjonen ved hjelp av TINAs analyse / veksel analyse / tidsfunksjon kommando.
Du kan sjekke at perioden er T = 20m og at VM = 311 V.
Egenskapene til 120 V AC spenningen i stikkontakten i USA:
Effektiv verdi: Veff = 120 V
Peak verdi: VM= √2 120 V = 169.68 V ≈ 170 V
Frekvens: f = 60 1 / s = 60 Hz
Vinkelfrekvens: ω = 2 * π * f = 376.8 rad / s ≈ 377 rad / s
Periode: T = 1 / f = 16.7 ms
Tidsfunksjon: v (t) = 170 sin (377 t)
Merk at i dette tilfellet kan tidsfunksjonen gis enten som v (t) = 311 sin (314 t + Φ) eller v (t) = 311 cos (314 t + Φ), siden i tilfelle av utgangsspenningen vi vet ikke den innledende fasen.
Initialfasen spiller en viktig rolle når flere spenninger er tilstede samtidig. Et godt praktisk eksempel er trefasesystemet, hvor tre spenninger med samme toppverdier, form og frekvens er til stede, hver av dem har en 120 ° faseskift i forhold til de andre. I et 60 Hz-nettverk er tidsfunksjonene:
vA(t) = 170 sin (377 t)
vB(t) = 170 sin (377 t - 120 °)
vC(t) = 170 sin (377 t + 120 °)
Følgende figur laget med TINA viser kretsen med disse tidsfunksjonene som TINAs spenningsgeneratorer.
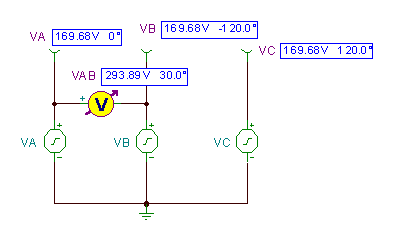

Spenningsforskjellen vAB= vA(TVB(t) vises som løst av TINAs analyse / veksel analyse / tidsfunksjon kommando.
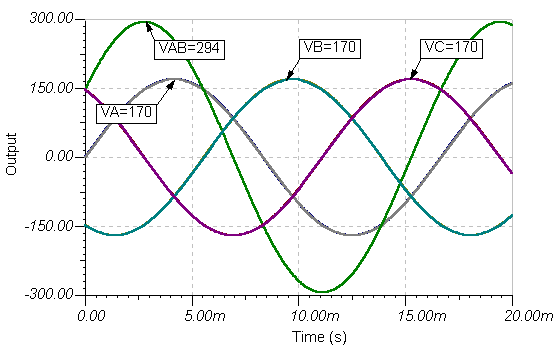

Legg merke til at toppen av vAB (t) er omtrent 294 V, større enn 170 V-toppene av vA(t) eller vB(t) spenninger, men ikke bare summen av deres toppspenninger. Dette skyldes faseforskjellen. Vi vil diskutere hvordan du beregner den resulterende spenningen (som er Ö3 * 170 @ 294 i dette tilfellet) senere i dette kapitlet og også i det separate Trefasesystemer kapittel.
Karakteristiske verdier av sinusformede signaler
Selv om et vekselstrømssignal varierer kontinuerlig i løpet av perioden, er det enkelt å definere noen karakteristiske verdier for å sammenligne en bølge med en annen: Disse er topp, gjennomsnitt og roten-middel-firkantet (rms) -verdiene.
Vi har allerede møtt toppverdien VM , som er rett og slett maksimal verdi av tidsfunksjonen, amplitude av sinusformet bølge.
Noen ganger brukes peak-to-peak (pp) verdien. For sinusformede spenninger og strømmer er topp-til-topp-verdien dobbelt toppverdien.
De gjennomsnittlig verdi av sinusbølgen er det aritmetiske gjennomsnittet av verdiene for den positive halv-syklusen. Det kalles også absolutt gjennomsnitt siden det er det samme som gjennomsnittet av den absolutte verdien av bølgeformen. I praksis møter vi denne bølgeformen ved likeretter sinusbølgen med en krets kalt en full bølge-likeretter.
Det kan vises at det absolutte gjennomsnittet av en sinusformet bølge er:
VAV= 2 / π VM ≅ 0.637 VM
Merk at gjennomsnittet av en hel syklus er null.
Den rms eller effektive verdien av en sinusformet spenning eller strøm tilsvarer ekvivalent DC-verdi som produserer den samme varmekraften. For eksempel produserer en spenning med en effektiv verdi på 120 V den samme oppvarmings- og belysningskraften i en lyspære som 120 V fra en likspenningskilde. Det kan vises at rms eller effektiv verdi av en sinusformet bølge er:

Vrms = VM / √2 ≅ 0.707 VM
Disse verdiene kan beregnes på samme måte for både spenninger og strømmer.
RMS-verdien er veldig viktig i praksis. Med mindre annet er angitt, er strømledningens spenninger (f.eks. 110V eller 220V) gitt i rms-verdier. De fleste AC-målere er kalibrert i rms og angir rms nivå.
Eksempel 1 Finn toppverdien av sinusformet spenning i et elektrisk nettverk med 220 V rms-verdi.
VM = 220 / 0.707 = 311.17 V
Eksempel 2 Finn toppverdien av sinusformet spenning i et elektrisk nettverk med 110 V rms-verdi.
VM = 110 / 0.707 = 155.58 V
Eksempel 3 Finn (absolutt) gjennomsnittet av sinusformet spenning hvis rms-verdien er 220 V.
Va = 0.637 * VM = 0.637 * 311.17 = 198.26 V
Eksempel 4 Finn absolutt gjennomsnitt av sinusformet spenning hvis rms-verdien er 110 V.
Spenningen fra spenningen fra eksempel 2 er155.58 V og dermed:
Va = 0.637 * VM = 0.637 * 155.58 = 99.13 V
Eksempel 5 Finn forholdet mellom absolutt gjennomsnitt (Va) og rms (V) -verdier for sinusformet bølgeform.
V / Va = 0.707 / 0.637 = 1.11
Vær oppmerksom på at du ikke kan legge til gjennomsnittsverdier i en vekselstrømskrets fordi det fører til feilresultater.
phasors
Som vi allerede har sett i forrige avsnitt, er det ofte nødvendig i AC-kretser å legge til sinusformede spenninger og strømmer av samme frekvens. Selv om det er mulig å legge til signaler numerisk ved hjelp av TINA, eller ved å benytte trigonometriske relasjoner, er det mer praktisk å bruke den såkalte fasor metode. En fasor er et komplekst tall som representerer amplitude og fase av et sinusformet signal. Det er viktig å merke seg at fasoren ikke representerer frekvensen, som må være den samme for alle fasorer.
En fasor kan håndteres som et komplekst tall eller representeres grafisk som en plan pil i det komplekse planet. Den grafiske representasjonen kalles et fasordiagram. Ved hjelp av fasordiagrammer kan du legge til eller trekke fasorer i et komplekst plan ved trekant eller parallellogramregel.
Det er to former for komplekse tall: rektangulær og polar.
Den rektangulære representasjonen er i forma + jb, hvor j = Ö-1 er den imaginære enheten.
Den polære representasjonen er i formen Aej j , hvor A er absoluttverdien (amplitude) og f er vinkelen fra fasoren fra den positive reelle akse, mot urviseren.
Vi vil bruke pin bokstaver for komplekse mengder.
La oss nå se hvordan du får den tilsvarende faseren fra en tidsfunksjon.
Først anta at alle spenninger i kretsen uttrykkes i form av cosinusfunksjoner. (Alle spenninger kan konverteres til det skjemaet.) Da fasor svarende til spenningen på v (t) = VM cos ( w t+f) er: VM = VMe jf , som også kalles den komplekse toppverdien.
For eksempel, vurder spenningen: v (t) = 10 cos ( w t + 30°)
Den tilsvarende fasoren er: 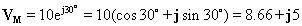
Vi kan beregne tidsfunksjonen fra en fasor på samme måte. Først skriver vi fasoren i polarform f.eks VM = VMe jr og deretter er den tilsvarende tidsfunksjonen
v (t) = VM (cos (wt+r).
For eksempel, vurdere fasoren VM = 10 - j20 V
Ta det til polar form:
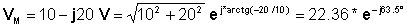
Og dermed er tidsfunksjonen: v (t) = 22.36 cos (wt - 63.5°) V
Fasorer brukes ofte til å definere komplekse effektive eller rms-verdier av spenninger og strømmer i vekselstrømskretser. Gitt v (t) = VMcos (wt+r) = 10cos (wt + 30°)
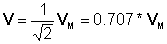
Numerisk:
v (t) = 10 * cos (wt-30°)
Den komplekse effektive (rms) verdien: V = 0.707 * 10 * e- j30° = 7.07 e- j30° = 6.13 - j 3.535
Omvendt: Hvis den komplekse effektive verdien av en spenning er:
V = - 10 + j 20 = 22.36 e j 116.5°
så den komplekse toppverdien: 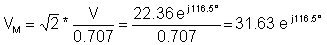
og tidsfunksjonen: v (t) = 31.63 cos ( wt + 116.5° ) V
En kort begrunnelse for ovennevnte teknikker er som følger. Gitt en tidsfunksjon
VM (cos ( w t+r), la oss definere kompleks tidsfunksjon som:
v (t) = VM e jr e jwt = VMe jwt = VM (cos (r) + j synd(r)) E jwt
hvor VM =VM e j r t = VM (cos (r) + j synd(r)) er bare fasoren introdusert ovenfor.
For eksempel, den komplekse tidsfunksjonen til v (t) = 10 cos (wt + 30°)
v (t) = VMe jwt = 10 e j30 e jwt = 10e jwt (cos (30) + j synd (30)) = e jwt (+ 8.66j5)
Ved å introdusere komplekse tidsfunksjonen har vi en representasjon med både en reell del og en imaginær del. Vi kan alltid gjenopprette den opprinnelige virkelige funksjonen av tid ved å ta den virkelige delen av resultatet: v (t) = Re {v(T)}
Den komplekse tidsfunksjonen har imidlertid den store fordelen at siden alle de komplekse tidsfunksjonene i de aktuelle kretsene har samme ejwt multiplikator, kan vi faktorere dette ut og bare jobbe med fasorene. I praksis bruker vi ikke ejwt del i det hele tatt - bare transformasjonene fra tidsfunksjonene til fasorene og tilbake.
For å demonstrere fordelen av å bruke fasorer, la oss se følgende eksempel.
Eksempel 6 Finn summen og forskjellen i spenningene:
v1 = 100 cos (314 * t) og v2 = 50 cos (314 * t-45°)
Først skriv fasene til begge spenningene:
V1M = 100 V2M= 50 e - j 45° = 35.53 - j 35.35
Derfor:
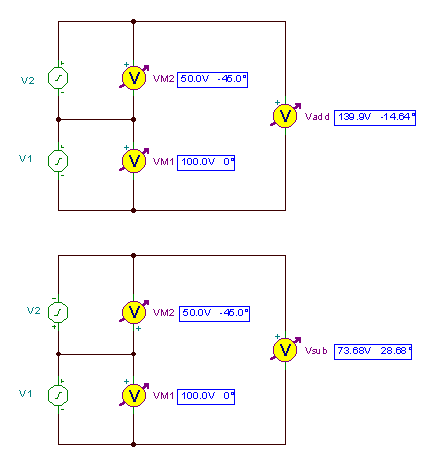
Vlegge til = V1M + V2M = 135.35 - j 35.35 = 139.89 e- j 14.63°
Vnedenfor = V1M - V2M = 64.65 + j35.35 = 73.68 og j 28.67°
og så fungerer tiden:
vlegge til(t) = 139.89 * cos (wt - 14.63°)
vnedenfor(t) = 73.68 * cos (wt + 28.67°)
Som dette enkle eksempelet viser, er metoden til phasors.is et ekstremt kraftig verktøy for å løse AC-problemer.
La oss løse problemet ved hjelp av verktøyene i TINAs tolk.
{beregning av v1 + v2}
v1: = 100
v2: = 50 * exp (-pi / 4 * j)
v2 = [35.3553-35.3553 * j]
v1add: = v1 + v2
v1add = [135.3553-35.3553 * j]
abs (v1add) = [139.8966]
radtodeg (arc (v1add)) = [- 14.6388]
{beregning av v1-v2}
v1sub: = v1-v2
v1sub = [64.6447 + 35.3553 * j]
abs (v1sub) = [73.6813]
radtodeg (arc (v1sub)) = [28.6751]
#beregning av v1+v2
importere matematikk som m
importer cmath som c
v1=100
v2=50*c.exp(complex(0,-c.pi/4))
print(“v2=”,v2)
vadd=v1+v2
print(“vadd=”,vadd)
print(“abs(vadd)=”,abs(vadd))
print(“degrees(arc(vadd))=”,m.degrees(c.phase(vadd)))
#beregning av v1-v2
vsub=v1-v2
print(“vsub=”,vsub)
print(“abs(vsub)=”,abs(vsub))
print(“degrees(arc(vsub))=”,m.degrees(c.phase(vsub)))
Amplituden og fase resultater bekrefter håndberegningene.
Nå kan vi sjekke resultatet ved hjelp av TINAs AC-analyse.
Før vi utfører analysen, la oss sørge for at Basisfunksjon for vekselstrøm Ia satt til cosinus i Redigeringsalternativer dialogboksen fra menyen Vis / Valg. Vi vil forklare rollen til denne parameteren på Eksempel 8.
Kretsene og resultatene:
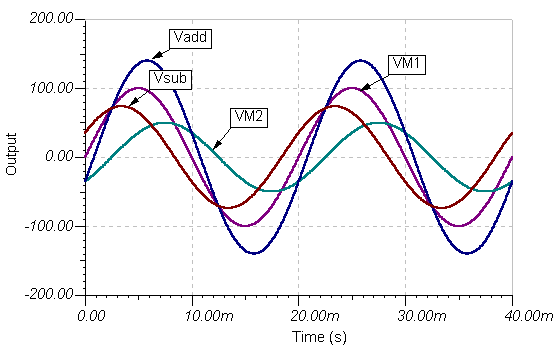
Igjen er resultatet det samme. Her er tidsfunksjonsgrafer:
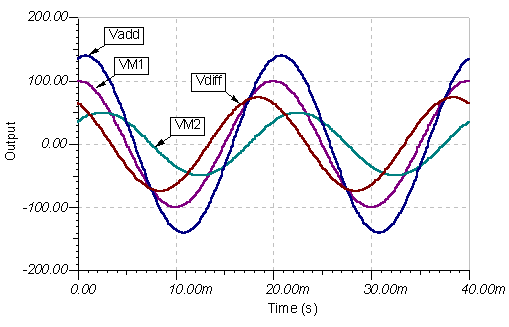
Eksempel 7 Finn summen og forskjellen i spenningene:
v1 = 100 sin (314 * t) og v2 = 50 cos (314 * t-45°)
Dette eksemplet gir et nytt spørsmål. Så langt har vi krevd at alle tidsfunksjoner skal gis som cosinusfunksjoner. Hva skal vi gjøre med en tidsfunksjon gitt som sinus? Løsningen er å omdanne sinusfunksjonen til en cosinusfunksjon. Ved hjelp av trigonometrisk forholdssyn (x) = cos (x-p/ 2) = cos (x-90°), kan vårt eksempel omformuleres som følger:
v1 = 100 cos (314t - 90°) og v2 = 50 cos (314 * t - 45°)
Nå er fasene av spenningene:
V1M = 100 e - j 90° = -100 j V2M= 50 e - j 45° = 35.53 - j 35.35
Derfor:
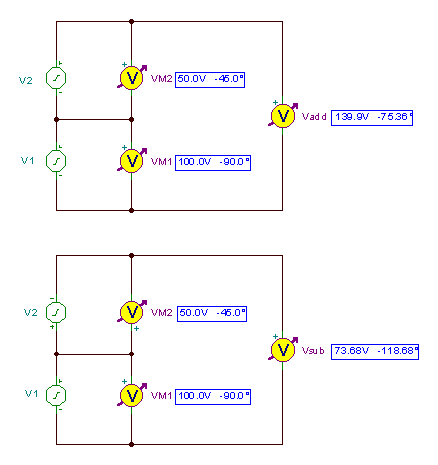
V legge til = V1M + V2M = 35.53 - j 135.35
V nedenfor = V1M - V2M = - 35.53 - j 64.47
og så fungerer tiden:
vlegge til(t) = 139.8966 cos (wt-75.36°)
vnedenfor(t) = 73.68 cos (wt-118.68°)
La oss løse problemet ved hjelp av verktøyene i TINAs tolk.
{beregning av v1 + v2}
v1: = - 100 * j
v2: = 50 * exp (-pi / 4 * j)
v2 = [35.3553 - 35.3553 * j]
v1add: = v1 + v2
v1add = [35.3553-135.3553 * j]
abs (v1add) = [139.8966]
radtodeg (arc (v1add)) = [- 75.3612]
{beregning av v1-v2}
v1sub: = v1-v2
v1sub = [- 35.3553 - 64.6447 * j]
abs (v1sub) = [73.6813]
radtodeg (arc (v1sub)) = [- 118.6751]
#beregning av v1+v2
importere matematikk som m
importer cmath som c
v1=100
v2=50*c.exp(complex(0,-c.pi/4))
print(“v2=”,v2)
vadd=v1+v2
print(“vadd=”,vadd)
print(“abs(vadd)=”,abs(vadd))
print(“degrees(arc(vadd))=”,m.degrees(c.phase(vadd)))
#beregning av v1-v2
vsub=v1-v2
print(“vsub=”,vsub)
print(“abs(vsub)=”,abs(vsub))
print(“degrees(arc(vsub))=”,m.degrees(c.phase(vsub)))
La oss sjekke resultatet med TINAs AC-analyse
Eksempel 8
Finn summen og forskjellen i spenningene:v1 = 100 synd (314 * t) og v2 = 50 synd (314 * t-45°)
Dette eksempelet bringer opp et annet problem. Hva om alle spenninger blir gitt som sinusbølger, og vi ønsker også å se resultatet som en sinusbølge ?. Vi kunne selvfølgelig konvertere begge spenningene til cosinusfunksjoner, beregne svaret og konvertere resultatet tilbake til en sinusfunksjon - men dette er ikke nødvendig. Vi kan lage fasorer fra sinusbølgene på samme måte som vi gjorde fra cosinusbølger, og deretter bare bruke amplituden og fasene som amplitude og fase av sinusbølger i resultatet.
Dette vil åpenbart gi samme resultat som å transformere sinusbølgene til cosinusbølger. Som vi kunne se i forrige eksempel, er dette tilsvarer å multiplisere med -j og deretter bruker cos (x) = sin (x-90°) for å transformere den tilbake til en sinusbølge. Dette tilsvarer å multiplisere med j. Med andre ord, siden -j × j = 1, vi kunne bruke fasene avledet direkte fra amplituder og faser av sinusbølger for å representere funksjonen og deretter returnere til dem direkte. Også resonnement på samme måte om de komplekse tidsfunksjonene, kan vi vurdere sinusbølger som de imaginære delene av komplekse tidsfunksjoner og supplere dem med cosinusfunksjonen for å opprette hele komplekse tidsfunksjonen.
La oss se løsningen på dette eksemplet ved å bruke sinusfunksjonene som basen til fasorene (transformere sin ( w t) til den reelle enhetsfasoren (1)).
V1M = 100 V2M= 50 e - j 45° = 35.53 - j 35.35
Derfor:
V legge til = V1M + V2M = 135.53 - j 35.35
V nedenfor = V1M - V2M = 64.47+ j 35.35
Merk at fasorene er nøyaktig det samme som i eksempel 6, men ikke tidsfunksjonene:
v3(t) = 139.9sin (wt - 14.64°)
v4(t) = 73.68sin (wt + 28.68°)
Som du kan se, er det veldig enkelt å oppnå resultatet ved hjelp av sinusfunksjoner, spesielt når de første dataene våre er sinusbølger. Mange lærebøker foretrekker å bruke sinusbølgen som basefunksjonen til fasorene. I praksis kan du bruke begge metodene, men ikke forveksle dem.
Når du lager fasene, er det svært viktig at alle tidsfunksjoner først konverteres til sinus eller cosinus. Hvis du startet fra sinusfunksjoner, bør dine løsninger være representert med sinusfunksjoner når du returnerer fra fasorer til tidsfunksjoner. Det samme gjelder når du starter med cosinusfunksjoner.
La oss løse det samme problemet ved hjelp av TINAs interaktive modus. Siden vi ønsker å bruke sinusfunksjoner som grunnlag for å lage fasene, må du sørge for at Basisfunksjon for vekselstrøm er satt til sinus i Redigeringsalternativer dialogboksen fra menyen Vis / Alternativ.
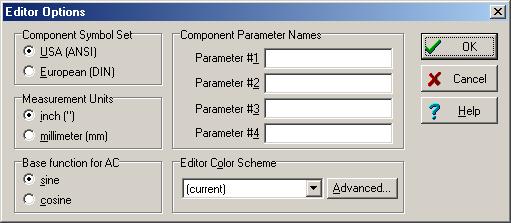

Kretsene for å lage summen og forskjellen på bølgeformene og resultatet:
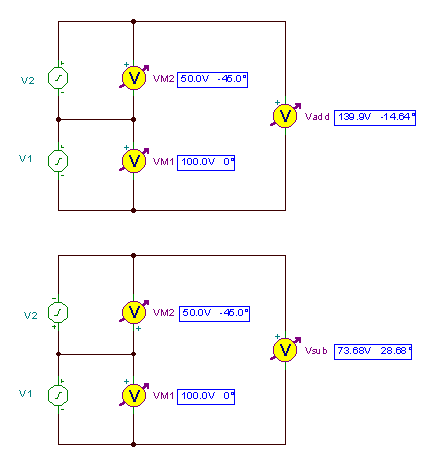
og tidsfunksjonene: