Кликнете или докоснете примерните схеми по-долу, за да извикате TINACloud и изберете режим Интерактивна DC, за да ги анализирате онлайн.
Кликнете или докоснете примерните схеми по-долу, за да извикате TINACloud и изберете режим Интерактивна DC, за да ги анализирате онлайн. Получете достъп до TINACloud, за да редактирате примерите или да създадете свои собствени схеми
Друг начин за опростяване на пълния набор от уравнения на Кирххоф е методът на мрежата или тока на веригата. Използвайки този метод, сегашният закон на Кирхоф се изпълнява автоматично, а уравненията на цикъла, които пишем, също удовлетворяват закона за напрежението на Кирхоф. Задоволяването на сегашния закон на Kirchhoff се постига чрез присвояване на затворени токови вериги, наречени мрежести или контурни токове, към всеки независим контур на веригата и използване на тези токове за изразяване на всички останали количества от веригата. Тъй като токовете на цикъла са затворени, токът, който се влива в възел, също трябва да изтича от възела; така че писането на уравнения на възли с тези течения води до идентичност.
Нека първо разгледаме метода на мрежести токове.
Първо отбелязваме, че методът на мрежовия ток е приложим само за „равнинни“ вериги. Планарните вериги нямат пресичащи проводници, когато са изтеглени в равнина. Често чрез пречертаване на схема, която изглежда непланарна, можете да определите, че тя всъщност е равнинна. За неплоски вериги използвайте метод на токов контур описани по-долу в тази глава.
За да обясните идеята за мрежести токове, представете клоните на веригата като „риболовна мрежа“ и присвойте мрежов ток на всяка мрежа на мрежата. (Понякога се казва също, че във всеки „прозорец“ на веригата е зададен затворен контур на тока.)
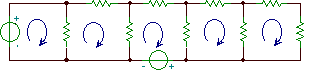  Схематичната диаграма   „Риболовната мрежа“ или графиката на веригата |
Техниката на представяне на схемата чрез обикновен чертеж, наречен a крива, е доста мощен. От Законите на Кирхоф не зависят от естеството на компонентите, можете да пренебрегнете конкретните компоненти и да замените в тях прости сегментни линии, наречени клонове от графиката. Представянето на схеми чрез графики ни позволява да използваме математическите техники теория на графите, Това ни помага да проучим топологичния характер на дадена верига и да определим независимите контури. Върнете се по-късно на този сайт, за да прочетете повече по тази тема.
Етапи на анализ на тока на мрежата:
Задайте мрежов ток на всяка мрежа. Въпреки че посоката е произволна, обичайно е да се използва посоката на часовниковата стрелка.
Прилагайте закона за напрежението (KVL) на Kirchhoff около всяка мрежа, в същата посока като мрежовите токове. Ако резисторът има два или повече мрежести тока през него, общият ток през резистора се изчислява като алгебраична сума на мрежовите токове. С други думи, ако ток, преминаващ през резистора, има същата посока като мрежовия ток на контура, той има положителен знак, в противен случай отрицателен знак в сумата. Източниците на напрежение се вземат предвид както обикновено, Ако тяхната посока е същата като мрежовия ток, напрежението им се приема за положително, иначе отрицателно, в уравненията на KVL. Обикновено за източници на ток през източника протича само един мрежест ток и този ток има същата посока като тока на източника. Ако това не е така, използвайте по-общия метод на токов цикъл, описан по-долу в този параграф. Не е необходимо да се пишат KVL уравнения за контури, съдържащи мрежести токове, присвоени на източници на ток.
Решете получените уравнения на веригата за мрежовите токове.
Определете всеки заявен ток или напрежение във веригата, като използвате мрежестите токове.
Нека илюстрираме методът по следния пример:
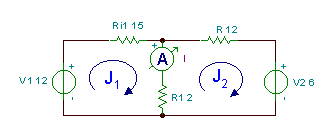
Намерете тока в схемата по-долу.
Виждаме, че в тази схема има две мрежи (или ляв и десен прозорец). Нека зададем мрежести токове J по посока на часовниковата стрелка J1 и J2 до окото. Тогава пишем уравненията на KVL, изразяващи напреженията през резисторите по закона на Ом:
-V1 + J1* (Ri1+R1) - J2*R1 = 0
V2 - J1*R1 + J2* (R + R1) = 0
Изразено в числа:
-12 + J1* 17 - J2* 2 = 0
6 - J1* 2 + J2* 14 = 0
Експрес J1 от първото уравнение: J1 = 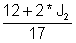

умножете по 17: 102 - 24 + 4 * J2 + 238 * J2 = 0 следователно J2 = 
и J1 = 
И накрая, необходимия ток:
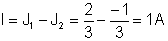
{Метод на текущата мрежа:}
Sys J1, J2
J1*(Ri1+R1)-J2*R1-V1=0
J1*R1+J2*(R1+R)+V2=0
края;
J1 = [666.6667m]
J2 = [- 333.3333m]
I: = J1-J2;
I = [1]
импортирайте numpy като n
#Използвайте метода на мрежовия ток!
#Имаме линейна система от уравнения, която искаме да решим
#за I1,I2:
#I1*(Ri1+R1)+I2*Ri1-V1=0
#-V1+I1*Ri1+I2*(Ri1+R)+V2=0
#Напишете матрицата на коефициентите:
A=n.array([[Ri1+R1,Ri1],[Ri1,Ri1+R]])
#Напишете матрицата на константите:
b=n.масив([V1,V1-V2])
x=n.linalg.solve(A,b)
I1=x[0]
I2=x[1]
print(“I1= %.3f”%I1)
print(“I2= %.3f”%I2)
I=I1
print(“I= %.3f”%I)
Нека проверим резултатите с TINA:
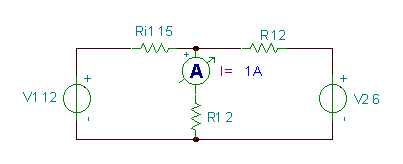

На следващо място, нека решим отново предишния пример, но с по-общия метод на контурните токове. Използвайки този метод, се наричат затворените токови контури контурни токове, са назначени не непременно на мрежите на веригата, а на произволни независими контури, Можете да гарантирате, че контурите са независими, като имате поне един компонент във всеки цикъл, който не се съдържа в никой друг цикъл. За равнинните вериги броят на независимите контури е същият като броя на окото, което е лесно да се види.
По-точен начин за определяне на броя на независимите бримки е следният.
Като се има предвид схема с b клони и N възли. Броят на независимите бримки l е:
l = b - N + 1
Това следва от факта, че броят на независимите уравнения на Кирхоф трябва да е равен на клоните във веригата, и вече знаем, че има само N-1 независими уравнения на възела Следователно общият брой на уравненията на Кирхоф е
b = N-1 + l и следователно l = b - N + 1
Това уравнение следва и от основната теорема на теорията на графовете, която ще бъде описана по-късно на този сайт.
Сега нека решим предишния пример отново, но по-просто, като използваме метода на контурния ток. С този метод сме свободни да използваме бримки в мрежи или всякакви други контури, но нека да поддържаме цикъла с J1 в лявата мрежа на веригата. За втория цикъл обаче избираме цикъла с J2, както е показано на фигурата по-долу. Предимството на този избор е, че J1 ще бъде равен на искания ток I, тъй като той е единственият токов цикъл, преминаващ през R1. Това означава, че не е необходимо да изчисляваме J2 изобщо. Обърнете внимание, че за разлика от „реалните“ токове, физическото значение на контурните токове зависи от това как ги причисляваме към веригата.
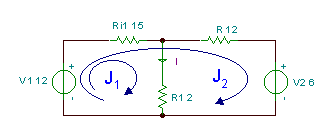

Уравненията на KVL:
J1 * (R1+Ri1) + J2 * R i1 - V1 = 0
-V1+ J1 * Ri1+ J2 * (R + Ri) + V2 = 0
и необходимия ток: I = J1
Numerically: J1*(15+2)+J2*15-12 = 0
-12 + J1 * 15 + J2 * (15 + 12) + 6 = 0
Експресирайте J2 от второто уравнение:
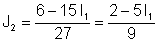
Заместване в първото уравнение:
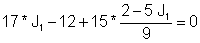
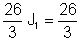
Следователно: J1 = I = 1 A
Други примери.
Пример 1
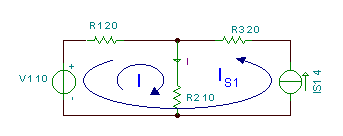
Намерете тока в схемата по-долу.
В тази схема използваме метода на контурните токове. В левия прозорец на веригата вземаме токов цикъл, с който се обозначаваме I тъй като тя е равна на искания ток. Другият токов контур е равен на източника на тока Is1, така че го обозначаваме директно като IS1.
Обърнете внимание, че посоката на този токов контур е не по посока на часовниковата стрелка, тъй като посоката му се определя от източника на ток. Въпреки това, тъй като този токов цикъл вече е известен, не е необходимо да се пише уравнението KVL за цикъла където IS1 е взето.
Следователно единственото уравнение за разрешаване е:
-V1 + I * R2 + R1 * (Аз - азS1) = 0
следователно
I = (V1 + R1 *IS1) / (R1 + R2)
числено
I=(10+20*4)/(20+10)=3 A
Можете също да генерирате този резултат, извиквайки символичния анализ на TINA от менюто Анализ / Символичен анализ / DC Резултат:
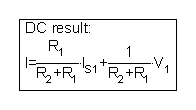
Или можете да разрешите уравнението KVL от интерпретатора:
| {Решение от преводача на TINA} {Използва се метод на мрежовия ток} Sys I -V1 + I * R2 + R1 * (I - IS1) = 0 края; I = [3] |
Следващият пример има 3 източника на ток и е много лесен за разрешаване чрез метода на контурните токове.
Пример 2
Намери напрежението V.
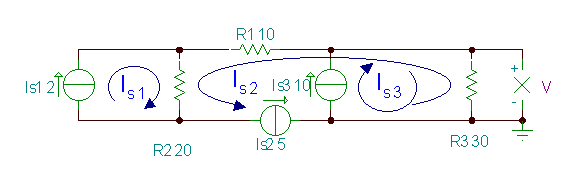

В този пример можем да изберем три контурни тока, така че всеки да преминава през само един източник на ток. Следователно, всичките три контура на тока са известни и трябва само да изразим неизвестното напрежение V, използвайки ги.
Осъществяване на алгебричната сума на токовете през R3:
V = (IS3 - АзS2) * R3= (10-5) * 30 = 150 V. Можете да потвърдите това с TINA:.
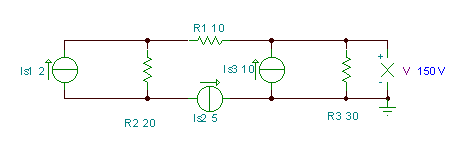

На следващо място, нека отново да се справим с проблем, който вече сме решили в Законите на Кирххоф намлява Метод на потенциалния възел глави.
Пример 3
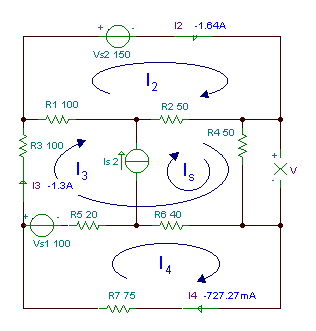
Намерете напрежението V на резистора R4.
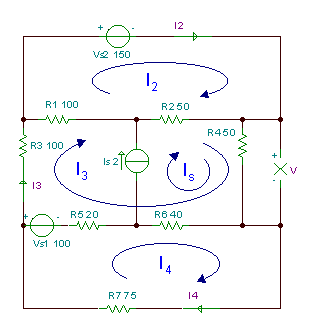

R1 = R3 = 100 ом, R2 = R4 = 50 ом, R5 = 20 ом, R6 = 40 ом, R7 = 75 ома.
Този проблем се нуждаеше от поне 4 уравнения, за да се реши в предишните глави.
Решавайки този проблем с метода на контурните токове, имаме четири независими контура, но при правилния избор на контурни токове един от контурните токове ще бъде равен на източника на ток.
Въз основа на токовете на цикъла, показани на фигурата по-горе, уравненията на цикъла са:
VS1+I4* (R5+R6+R7) - АзS*R6 -I3* (R5 + R6) = 0
VS2 - Аз3* (R1+R2) - АзS*R2 + I2* (R1 + R2) = 0
-VS1 + I3* (R1 + R2 + R3 + R4 + R5 + R6) + IS* (R2 +R4 + R6) - Аз4* (R5 + R6) - Аз2* (R1 + R2) = 0
Неизвестното напрежение V може да се изрази от контурните токове:
V = R4 * (I2 + I3)
Изразено в числа:
100 + I4* 135-2 * 40-I3* 60 = 0
150 + I2* 150-2 * 50-I3* 150 = 0
-100 + I3* 360 + 2 * 140-I4* 60-I2* 150 = 0
V = 50 * (2 + I3)
Можем да използваме правилото на Крамер за решаване на тази система от уравнения:
I4 = D3/D
където D е определящият фактор на системата. D4, определящ фактор за I4, се образува чрез замяна на дясната страна на системата се поставя за колоната от I4коефициенти.
Системата от уравнения в подредена форма:
- 60 * I3 + 135 * I4= -20
* Аз 1502* Аз -1503 = - 50
* Аз -1502+ 360 * I3 - 60 * I4= - 180
Така че определящ D:
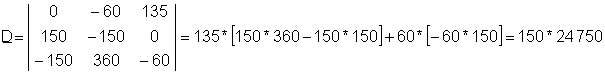
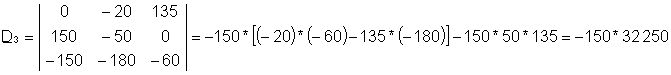
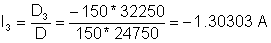
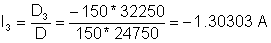
Решението на тази система от уравнения е:
V = R4* (2 + I3) = 34.8485 V
Можете да потвърдите отговора чрез резултата, изчислен от TINA.
Сис I2, I3, I4
Vs2+I2*(R1+R2)-R2*Is-I3*(R1+R2)=0
-Vs1+I3*(R1+R2+R3+R4+R5+R6)+Is*(R2+R4+R6)-I2*(R1+R2)-I4*(R5+R6)=0
Vs1+I4*(R5+R6+R7)-Is*R6-I3*(R5+R6)=0
края;
I2 = [- 1.6364]
I3 = [- 1.303]
I4 = [- 727.2727m]
V: = R4 * (Е + I3);
V = [34.8485]
импортирайте numpy като n
#Имаме линейна система от уравнения, която искаме да решим
#за I1,I2,I3,I4:
#I1=Е
#Vs2+I2*(R1+R2)-R2*I1-I3*(R1+R2)=0
#-Vs1+I3*(R1+R2+R3+R4+R5+R6)+I1*(R2+R4+R6)-I2*(R1+R2)-I4*(R5+R6)=0
#Vs1+I4*(R5+R6+R7)-I1*R6-I3*(R5+R6)=0
#Напишете матрицата на коефициентите:
A=n.array([[1,0,0,0],[-R2,R1+R2,-(R1+R2),0],[R2+R4+R6,-(R1+R2),R1+R2+R3+R4+R5+R6,-(R5+R6)],[-R6,0,-(R5+R6),R5+R6+R7]])
#Напишете матрицата на константите:
b=n.масив([Е,-Vs2,Vs1,-Vs1])
x=n.linalg.solve(A,b)
I1,I2,I3,I4=x[0],x[1],x[2],x[3]
print(“I1= %.5f”%I1) #x[0]=I1
print(“I2= %.5f”%I2) #x[1]=I2
print(“I3= %.5f”%I3) #x[2]=I1
print(“I4= %.5f”%I4) #x[3]=I2
V=R4*(I1+I3)
print(“V= %.5f”%V)
В този пример всеки неизвестен токов цикъл е разклонен ток (I1, I3 и I4); така че е лесно да се провери резултатът в сравнение с резултатите от DC анализа на TINA.