 Feu clic o Toqueu els circuits d'exemple a continuació per invocar TINACloud i seleccioneu el mode DC interactiu per analitzar-los en línia.
Feu clic o Toqueu els circuits d'exemple a continuació per invocar TINACloud i seleccioneu el mode DC interactiu per analitzar-los en línia. Obtingueu un accés de baix cost a TINACloud per editar els exemples o crear els vostres propis circuits
En aquest i en els capítols següents, presentarem un tema molt important: CA, o Corrent altern. El nom de corrent altern no és molt precís i normalment cobreix circuits amb tensions i corrents sinusoïdals; no obstant això, el corrent altern pot també significar qualsevol forma d'ona de corrent arbitrària. La importància de la tensió AC és que aquest tipus de tensió s’utilitza per a la font d’energia elèctrica principal a les llars i la indústria a tot el món. També és la base de moltes aplicacions electròniques, de telecomunicacions i industrials.
Per gestionar les formes d'ona sinusoïdals i els circuits associats a ells, utilitzarem un mètode senzill i elegant anomenat mètode de fasors. Els fases es basen en les propietats dels nombres complexos, que són ideals per representar quantitats sinusoïdals. En aquest capítol, es resumirà els principals fets sobre els números complexos i les seves operacions. També mostrarem com l’interpret de TINA facilita els càlculs amb números complexos.
Els números complexos consten de dues parts, a part real (x), que és un nombre real i un anomenat part imaginària (y), que és un nombre real multiplicat per 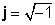
z = x + jy
where 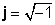
Exemples de nombres complexos:
z 1 = 1 + j
z 2 = 4-2 j
z 3 = 3- 5j
Els números complexos van ser introduïts originalment al segle XVII per representar les arrels dels polinomis que no es podien representar només amb nombres reals. Per exemple, les arrels de l’equació x2 + 2x + 2 = 0 només es pot descriure com 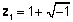
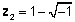
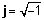
Representació geomètrica de nombres complexos
Forma rectangular
Com que un nombre complex sempre es pot separar en les seves parts reals i complexes, podem representar un nombre complex com un punt en un pla bidimensional. La part real d’un nombre complex és la projecció del punt sobre l’eix real, i la part imaginària del número és la projecció sobre l’eix imaginari. Quan un nombre complex es representa com la suma de parts reals i imaginàries, diem que està dins rectangular or forma algebraica.
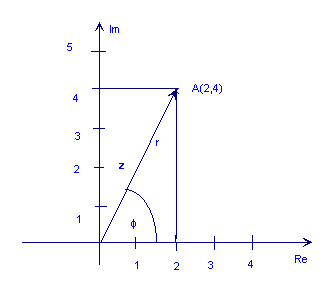
La figura següent mostra el nombre complex z = 2 + 4j
Forma polar i exponencial
Com es pot veure a la figura de dalt, el punt A també es pot representar per la longitud de la fletxa, r (també anomenat valor absolut, magnitud o amplitud) i el seu angle (o fase), φ relativa en sentit antihorari amb l’eix horitzontal positiu. Aquest és el polar forma d’un nombre complex. Es denota com r ∠ φ.
El següent pas és molt important. També es pot escriure un nombre complex en forma polar exponencial forma:
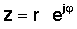
Aquesta expressió senzilla és distintiva pel fet que té un nombre imaginari en l’exponent en lloc del nombre real habitual. Aquesta complexa exponencial es comporta molt diferent de la funció exponencial amb un argument real. Mentre ex creix ràpidament en magnitud per augmentar x> 0 i disminueix per x <0, la funció 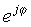
La fórmula d'Euler proporciona un vincle unificador entre les formes rectangulars, polars i exponencials dels nombres complexos:
z = x + jy = re jφ = r (cos φ + j sense φ )
where 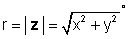
i φ = tan-1 (i / x).
Per al nostre exemple anterior, z = 2 + 4j:
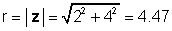
φ = tan-1 (4 / 2) = 63.4 °
per tant 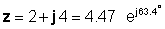
O viceversa:
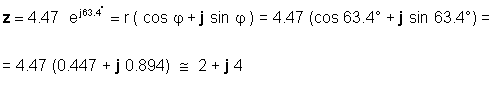
Haureu de ser capaç d’utilitzar els dos formularis, segons l’aplicació. Per exemple, la suma o la resta són òbviament més fàcils de fer quan els nombres són de forma rectangular, mentre que la multiplicació i la divisió són més fàcils de fer quan els nombres són de forma exponencial.
Operacions amb números complexos
Les operacions que es poden fer amb nombres complexos són similars a les de nombres reals. A continuació es resumeixen les regles i algunes definicions noves.
Operacions amb j
Les operacions amb j simplement segueix la definició de la unitat imaginària,


Per poder treballar ràpidament i amb precisió, haureu de memoritzar aquestes regles:
j 2 = -1
j 3 =-j
j 4 =1
1/j = -j
j2 = -1 simplement segueix la definició de 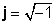
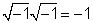
Per a 1 /j, multiplicem 1 /jby j / j = 1 i obtindreu j/ (jj) = j / (- 1) = -j.
Conjugat complex
El complex conjugat d’un nombre complex es deriva fàcilment i és bastant important. Per obtenir el conjunt conjugat complex d’una forma rectangular, simplement canvieu el signe de la part imaginària. Per fer-ho per un nombre en forma exponencial, canvieu el signe de l'angle del nombre complex mantenint el seu valor absolut igual.
El conjugat complex d’un nombre complex z és sovint denotat per z*.
Donat el nombre complex z= a + jb, el seu conjugat complex és z*= a– jb.
If z es dóna en forma exponencial, 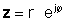
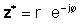
Utilitzant les definicions anteriors, és fàcil veure que un nombre complex multiplicat pel seu conjugat complex proporciona el quadrat del valor absolut del nombre complex:
zz* = r2 = a2 + b2
A més, sumant o restant qualsevol nombre complex i el seu conjugat, obtenim les següents relacions:
z + z * = 2a
per tant
Re (z) = a = ( z + z * ) / 2
De la mateixa manera:
z - z * =j2b
per tant
Jo sóc(z) = b = ( z -z * ) / 2j
Prova:
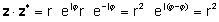
o multiplicar les parts reals i imaginàries i utilitzar-les j2= -1
zz* = (a + jb) (a - jb) = a2+a jb - a jb - jbjb = a2j2 = a2 + b2
z + z* = a + jb + a - jb = 2a
z - z*= a + jb - a + jb =j2b
Exemples numèrics:
De forma rectangular:
z = 3 + j4
z* = 3– j4
zz * = 9 + 16 = 25
En forma polar
z = 5 ∠ 53.13 °
z * = 5 ∠- 53.13 °
De forma exponencial:
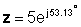
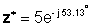
Suma i resta
La suma i la resta de nombres complexos és senzilla; només cal que sumem les parts reals i les imaginàries per separat. Per exemple, si
z1 = 3 - 4j i z2 = 2 + 3j
llavors
z1 + z2 = 3 - 4j + 2 + 3j = 3 + 2 - 4j + 3j = 5 - j
z1 - z2 = 3 - 4j - 2 - 3j = 3 - 2 - 4j - 3j = 1 - j7
Evidentment, hauríem d’utilitzar la forma rectangular per a aquestes operacions. Si els nombres es donen de forma exponencial o polar, hauríem de transformar-los primer en forma rectangular mitjançant la fórmula d’Euler, tal com s’ha donat anteriorment.
Multiplicació
Hi ha dos mètodes per multiplicar nombres complexos -
Multiplicació de nombres complexos donats de forma rectangular
Per dur a terme l’operació, simplement multipliqueu les parts reals i imaginàries d’un número al seu torn per les parts reals i imaginàries de l’altre número i utilitzeu la identitat j2 = -1.
z1z2 = (a1 + jb1) (a2 + jb2) = a1 a2 + jb1a2+ jb2a1 - b1b2 = a1 a2- b1b2 + j(b1a2+ jb2a1)
Quan els números complexos es donen numèricament, no cal utilitzar la fórmula anterior. Per exemple, anem
z1 = 3 - 4j i z2 = 2 + 3j
Amb la multiplicació directa dels components:
z1z2 = (3 - 4j) (2 + 3j) = 6-8j +9j + 12 = 18 + j
o utilitzant la fórmula: z1z2 = a1 a2- b1b2 + j(b1a2+ b2a1)
z1z2 = 6 + 12 + j (-8 + 9) = 18 + j
Creiem que és més probable que feu un error si utilitzeu la fórmula que si multipliqueu els components directament.
z1: = 3-4 * j
z2: = 2 + 3 * j
z1 * z2 = [18 + 1 * j]
importar matemàtiques com m
importar cmath com a c
z1=complex('3-4j')
z2=complex('2+3j')
imprimir ("z1*z2=",z1*z2)
Multiplicació de nombres complexos donats en forma polar o exponencial
Per dur a terme aquesta operació, multipliqueu els valors absoluts i afegiu els angles dels dos números complexos. Deixar:
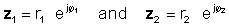
A continuació, utilitzant la regla de multiplicació de funcions exponencials:
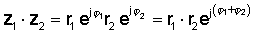
o en forma polar
z1 z2 = r1 r2 ∠ φ1 + φ2
Nota: ja hem utilitzat aquesta regla quan hem calculat zz *més amunt Com que l’angle del conjugat té el signe oposat a l’angle original, un nombre complex multiplicat pel seu propi conjugat és sempre un nombre real; és a dir, el quadrat del seu valor absolut: zz * = r2
Per exemple, deixeu:
z1 = 5 ∠ 30 ° i z2 = 4 ∠ -60 °
llavors
z1z2 = 20 ∠ -30 °
o de forma exponencial
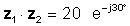
La multiplicació és, òbviament, més senzilla quan els números estan en forma polar o exponencial.
Tanmateix, si els nombres complexos es donen de forma rectangular, haureu de considerar la realització de la multiplicació directament com es mostra més amunt, ja que hi ha passos addicionals si convertiu els números en forma polar abans de multiplicar-los. Un altre factor a considerar és si voleu que les respostes siguin en forma rectangular o en forma polar / exponencial. Per exemple, si els dos nombres són de forma rectangular, però voleu que el seu producte sigui en forma polar, té sentit convertir-los immediatament i multiplicar-los.
divisió
Hi ha dos mètodes per dividir nombres complexos:
Divisió de nombres complexos donats de forma rectangular
Per dur a terme l’operació, multiplica el numerador i el denominador pel conjugat del denominador. El denominador es converteix en un nombre real i la divisió es redueix a la multiplicació de dos nombres complexos i una divisió per un nombre real, el quadrat del valor absolut del denominador.
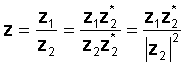
Per exemple, deixeu:
z1 = 3 - 4j i z2 = 2 + 3j
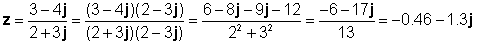
Comproveu aquest resultat amb l’interpret de TINA:
z1: = 3-4 * j
z2: = 2 + 3 * j
z1 / z2 = [- 461.5385m-1.3077 * j]
importar matemàtiques com m
importar cmath com a c
z1=complex('3-4j')
z2=complex('2+3j')
imprimir ("z1/z2=",z1/z2)
Divisió de nombres complexos donats en forma polar o exponencial
Per dur a terme l'operació, divideixi els valors absoluts (magnituds) i resti l'angle del denominador a l'angle del numerador. Deixar:
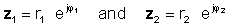
llavors utilitzant la regla de divisió de funcions exponencials
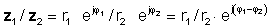
o en forma polar
z 1 / z2 = r1 / r2 ∠ φ 1- φ 2
Per exemple, deixeu:
z 1 = 5 ∠ 30 ° i z 2 = 2 ∠ -60 °
llavors
z 1 / z2 = 2.5 ∠ 90 °
o en formes exponencials i rectangulars
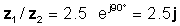
Comproveu aquest resultat amb l’interpret de TINA:
z1: = 5 * exp (j * degtorad (30))
z2: = 2 * exp (j * degtorad (-60))
z1 / z2 = [0 + 2.5 * j]
importar matemàtiques com m
importar cmath com a c
z1=5*(c.exp(complex(0,m.radians(30))))
z2=2*(c.exp(complex(0,m.radians(-60))))
imprimir ("z1/z2=",z1/z2)
La divisió és òbviament més simple quan els nombres estan en forma polar o exponencial.
Tanmateix, si els nombres complexos es donen de forma rectangular, haureu de considerar la realització de la divisió directament mitjançant el mètode conjugat complex com es mostra més amunt, ja que hi ha passos addicionals si convertiu els números en forma polar abans de dividir-los. Un altre factor a considerar és si voleu que les respostes siguin en forma rectangular o en forma polar / exponencial. Per exemple, si els dos nombres tenen forma rectangular, però voldríeu que el seu quocient sigui en forma polar, té sentit convertir-los immediatament i després dividir-los.
Ara il·lustrem l’ús de nombres complexos per problemes numèrics. Com és habitual, revisarem les nostres solucions mitjançant l’interpret de TINA. L'intèrpret treballa amb radiants, però té funcions estàndard per a la conversió de radiants en graus o viceversa.
Exemple 1 Cerqueu la representació polar:
z = 12 - j 48
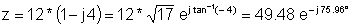
z: = 12-j * 48;
abs (z) = [49.4773]
arc (z) = [- 1.3258]
radtodeg (arc (z)) = [- 75.9638]
importar matemàtiques com m
importar cmath com a c
z=12-complex (48j)
imprimir ("abs(z)=",abs(z))
print("arc(z)="",c.phase(z))
imprimir ("graus (arc (z)) =", m.graus (fase c (z)))
Exemple 2 Cerqueu la representació rectangular:
z = 25 e j 125 °
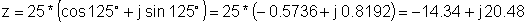
z: = 25 * exp (j * (degtorad (125)));
z = [- 14.3394 + 20.4788 * j]
Re (z) = [- 14.3394]
Im (z) = [20.4788]
importar matemàtiques com m
importar cmath com a c
z=25*c.exp(complex(0,m.radians(125)))
imprimir ("z=",z)
print("real(z)="",z.real)
print("imag(z)="",z.imag)
Exemple 3 Cerqueu la representació polar dels següents números complexos:
z 1 = 12 + j 48 z2 = 12 - j48 z3= -12 + j 48 z4= -12 - j 48
Els valors absoluts dels quatre nombres són els mateixos, perquè el valor absolut és independent dels signes. Només els angles són diferents.
z1: = 12 + j * 48;
abs (z1) = [49.4773]
arc (z1) = [1.3258]
radtodeg (arc (z1)) = [75.9638]
z2: = 12-j * 48;
abs (z2) = [49.4773]
arc (z2) = [- 1.3258]
radtodeg (arc (z2)) = [- 75.9638]
z3: = - 12 + j * 48;
abs (z3) = [49.4773]
arc (z3) = [1.8158]
radtodeg (arc (z3)) = [104.0362]
z4: = - 12-j * 48:
abs (z4) = [49.4773]
arc (z4) = [- 1.8158]
radtodeg (arc (z4)) = [- 104.0362]
importar matemàtiques com m
importar cmath com a c
z1=complex('12+48j')
imprimir ("abs(z1)="", abs(z1))
print(“arc(z1)=",c.phase(z1))
imprimir ("graus (arc (z1)) =", m.graus (fase c (z1)))
z2=complex('12-48j')
imprimir ("abs(z2)="", abs(z2))
print(“arc(z2)=",c.phase(z2))
imprimir ("graus (arc (z2)) =", m.graus (fase c (z2)))
z3=complex('-12+48j')
imprimir ("abs(z3)="", abs(z3))
print(“arc(z3)=",c.phase(z3))
imprimir ("graus (arc (z3)) =", m.graus (fase c (z3)))
z4=complex('-12-48j')
imprimir ("abs(z4)="", abs(z4))
print(“arc(z4)=",c.phase(z4))
imprimir ("graus (arc (z4)) =", m.graus (fase c (z4)))
La funció arc () de TINA determina l’angle de qualsevol nombre complex, situant-lo automàticament correctament en un dels quatre quadrants.
Tingueu cura amb el bronzejat-1 funció per trobar l'angle, ja que es restringeix als angles de retorn només al primer i quart quadrants (–90 °φ<90 °).
Des z1 es troba al primer quadrant del sistema de coordenades, el càlcul és:
α 1 = tan-1(48 / 12) = tan-1(4) = 75.96 °
Des z4 es troba al tercer quadrant del sistema de coordenades, tan-1no retorna l’angle correctament. El càlcul d'angle és:
α 4 = 180 ° + 75.96 ° = 255.96 ° o -360 ° + 255.96 ° = - 104.04 °, que és el mateix que calcula TINA.
z2 es troba al quart quadrant del sistema de coordenades El càlcul d'angle és:
α 2 = tan-1(-48 / 12) = tan-1(-4) = -75.96 °
z3, tanmateix, es troba en el quadrant 2nd del sistema de coordenades, tan tan-1 no retorna l’angle correctament. El càlcul d'angle és:
α 3 = 180 ° -75.96 ° = 104.04 °.
Exemple 4 Tenim dos números complexos: z1= 4 - j 6 i z2 = 5 ej45 ° .
Cercar z3 = z1 + z2; z4 = z1 - z2; z5 = z1 * z2; z6 = z1 / z2
Primer solucionem el problema mitjançant l’interpret de TINA
{Solució de l'intèrpret de TINA} |
Observeu com TINA maneja sense esforç els dos números complexos donats en diferents formes.
La solució és més complicada sense l'intèrpret. Per tal de poder comparar els diferents mètodes de multiplicació i divisió, primer determinarem la forma polar de z1 i la forma rectangular de z2 .
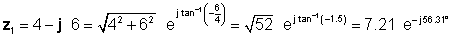
A continuació, trobem les quatre solucions utilitzant primer les formes més fàcils: rectangular per sumar i restar, i exponencial per a la multiplicació i la divisió:
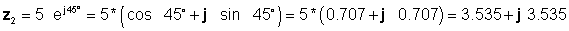
z 3 = z1 + z2 = 4 - j 6 + 3.535 + j 3.535 = 7.535 - j2.465
z 4 = z1 - z2 = 4 - j 6 - 3.535 - j 3.535 = 0.465 - j9.535
z 5 = z1 * z2 = 7.21 * 5 * ej(-56.31 ° + 45 °) = 36.05 e -j11.31 ° = 36.03 * (cos (-11.31 °) +j* sin (-11.31 °))
z 5 = 35.33 - j 7.07
z 6 = z1/z2= (7.21 / 5) * e j (-56.31 ° -45 °) = 1.442 e - j 101.31 ° = 1.442 (cos (-101.31 °) +j* sin (-101.31 °))
z 6 = -0.2828 - j 1.414
que coincideixen amb els resultats obtinguts amb l’Interpret de TINA.
La multiplicació d’una forma rectangular:
z 5 =z1*z2 = (4-j6) * 3.535 * (1 +j) = 7.07 * (2-j3) * (1 +j) = 7.07 * (2-j3+j2 + 3) = 7.07 * (5-j) = 35.35-j7.07
Finalment, la divisió es fa de forma rectangular:
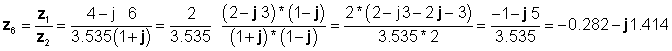
que coincideixen amb els resultats anteriors.
