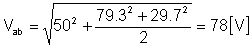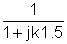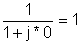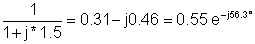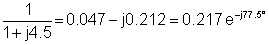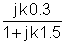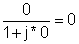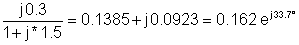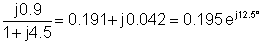Feu clic o Toqueu els circuits d'exemple a continuació per invocar TINACloud i seleccioneu el mode DC interactiu per analitzar-los en línia. Obtingueu un accés de baix cost a TINACloud per editar els exemples o crear els vostres propis circuits
El Teorema de Fourier estableix que qualsevol forma d'ona periòdica es pot sintetitzar afegint termes sinusoïdals i cosinus ponderats adequadament de diverses freqüències. El teorema està ben cobert en altres llibres de text, de manera que només resumirem els resultats i mostrarem alguns exemples.
Sigui f (t) = f (t) la nostra funció periòdica ±nT) on T és el temps d’un període i n és un nombre enter.
w0= 2p/ T la freqüència angular fonamental.
Pel Teorema de Fourier, la funció periòdica es pot escriure com a suma següent:
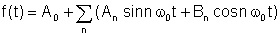
where 
An i Bn són els Coeficients de Fourier i la suma és la Sèries de Fourier.
Una altra forma, probablement una mica més pràctica:
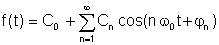
where
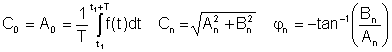
A0 = C0 és el valor DC o mitjà, A1, B1 i C1 són els components fonamentals i els altres són els termes harmònics.
Tot i que només es poden requerir uns quants termes aproximats a algunes formes d'ona, altres requereixen molts termes.
Generalment, com més termes s’incloguin, millor serà l’aproximació, però per a formes d’ona que contenen passos, com impulsos rectangulars, la Fenomen de Gibbs entra en joc. A mesura que augmenta el nombre de termes, la superació de dades es concentra en un període de temps cada vegada menor.
An fins i tot funcionen f (t) = f (-t) (simetria de l’eix) requereix només termes cosinus.
An funció estranya f (t) = - f (-t) (simetria puntual) només requereix termes sinus.
Una forma d’ona amb simetria de mirall o de mitja ona només té estrany harmònics en la seva representació de Fourier.
Aquí no tractarem l'expansió de la sèrie de Fourier, sinó que només utilitzarem una suma determinada de sinus i cosinus com a excitació per a un circuit.
En els capítols anteriors d’aquest llibre, hem tractat l’excitació sinusoïdal. Si el circuit és lineal, el Teorema de la superposició és vàlid. Per a una xarxa amb excitació periòdica nonsusoidal, la superposició ens permet calculeu els corrents i les tensions deguts a cada terme sinusoide de Fourier un per un. Quan es calculen totes, finalment resumim els components harmònics de la resposta.
És una mica complicat determinar els diferents termes de les tensions i corrents periòdics i, de fet, pot produir una sobrecàrrega d'informació. A la pràctica, ens agradaria simplement fer mesures. Podem mesurar els diferents termes harmònics mitjançant a analitzador harmònic, analitzador d’espectres, analitzador d’ones o analitzador de Fourier. Totes aquestes són complicat i probablement produirà més dades de les necessàries. De vegades és suficient descriure un senyal periòdic només segons els seus valors mitjans. Però hi ha diversos tipus de mesures mitjanes.
MITJANA VALUES
Mitjana senzilla or DC el terme va ser vist a la representació de Fourier com A0
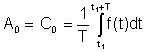
Aquesta mitjana es pot mesurar amb instruments com el Deprez Instruments de corrent continu
Valor efectiu or rms (quadrat mitjà arrel) té la definició següent:
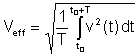
Aquest és el valor mitjà més important perquè la calor dissipada en resistències és proporcional al valor efectiu. Molts voltímetres digitals i alguns analògics poden mesurar el valor efectiu de tensions i corrents.
Mitjana absoluta
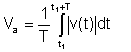
Aquesta mitjana ja no és important; els instruments anteriors mesuraven aquesta forma de mitjana.
Si coneixem la representació de Fourier d'una tensió o una forma d'ona de corrent, també podem calcular els valors mitjans de la manera següent:
Mitjana senzilla or DC el terme va ser vist a la representació de Fourier com A0 = C0
Valor efectiu or rms (quadrat mitjà arrel) és, després d'integrar la tensió de Fourier:
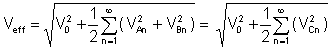
El klirr factor és una ràtio molt important entre els valors mitjans:
És la relació del valor efectiu dels termes harmònics superiors al valor efectiu de l'harmònic fonamental:
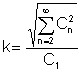
Sembla que hi ha una contradicció aquí: resolem la xarxa en termes de components harmònics, però mesurem quantitats mitjanes.
Il·lustrem el mètode amb exemples senzills:
Exemple 1
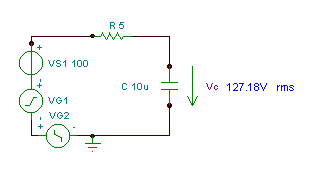
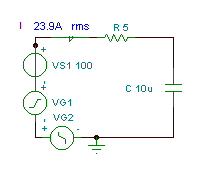
Cerqueu la funció de temps i el valor efectiu (rms) de la tensió vC(t)
si R = 5 ohm, C = 10 mF i v (t) = (cos 100 + 200 (w0t) + 30 cos (3 w0t - 90 °)) V, on és la freqüència angular fonamental w0= 30 krad / s.
Proveu d'utilitzar el teorema de superposicions per solucionar el problema.
El primer pas és trobar la funció de transferència en funció de la freqüència. Per senzillesa, utilitzeu la substitució: s = j w
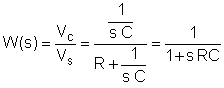
Ara substituïu els valors dels components i s = jk w0on k = 0; 1; 3 en aquest exemple i w0= 30 krad / s. En V, A, ohm, mUnitats F i Mrad / s:
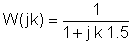
És útil utilitzar una taula per organitzar els passos de la solució numèrica:
k | W (jk) = |
0 |
|
1 |
|
3 |
|
Podem resumir els passos de la solució de superposició en una altra taula. Com ja hem vist, per trobar el valor màxim complex d'un component, hauríem de multiplicar el valor màxim complex del component de l'excitació pel valor de la funció de transferència complexa:
k | V | W | VCk |
0 | 100 | 1 | 100 |
1 | 200 | 0.55e-J56.3° | 110e-J56.3° |
3 | 30e-J90° | 0.217e-J77.5° | 6.51e-J167.5° |
I finalment podem donar la funció del temps coneixent els valors punta complexos dels components:
vC(t) = 100 + 110 cos (w0t - 56.3°) + 6.51 cos (3w0t - 167.5°) V
El valor rms (efectiu) de la tensió és:
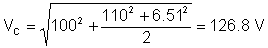
Com podeu veure, l’instrument de mesura de TINA mesura aquest valor eficaç.
Exemple 2
Cerqueu la funció del temps i el valor efectiu (rms) de la i (t) actual
si R = 5 ohm, C = 10 mF i v (t) = (cos 100 + 200 (w0t) + 30 cos (3w0t - 90 °)) V on es troba la freqüència angular fonamental w0= 30 krad / s.
Intenteu resoldre el problema fent servir el teorema de la superposició.
 |
Els passos de la solució són similars a l’exemple 1, però la funció de transferència és diferent.
Ara substitueix els valors numèrics i s = jk w0,on k = 0; 1; 3 en aquest exemple.
En V, A, ohm, mUnitats F i Mrad / s:
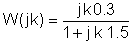
És útil utilitzar una taula durant la solució numèrica:
k | W (jk) = |
0 | |
1 | |
3 | |
Podem resumir els passos de la superposició en una altra taula. Com ja hem vist, per trobar el valor màxim d’un component, hauríem de multiplicar el valor màxim complex d’aquest component de l’excitació pel valor de la funció de transferència complexa. Utilitzeu els valors de pic complexos dels components de l'excitació:
k | VSk | W(jk) | Ik |
0 | 100 | 0 | 0 |
1 | 200 | 0.162 ij33.7° | 32.4 ij33.7° |
3 | 30 i-J90° | 0.195 ij12.5° | 5.85 i-J77.5° |
I finalment, coneixent els valors màxims complexos dels components, podem afirmar la funció de temps:
i (t) = cos 32.4 (w0t + 33.7°) + 5.85 cos (3w0t - 77.5°) [A]
Tvalora el valor actual:
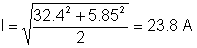
Sovint podeu fer un control sanitari per part de la solució. Per exemple, un condensador pot tenir un voltatge de corrent continu però no un corrent continu.
Exemple 3
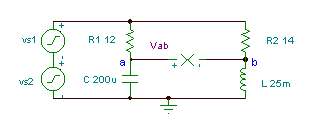
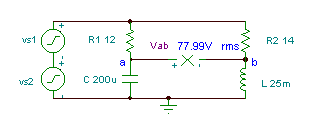
Obteniu la funció de temps de la tensió Vab if R1= 12 ohm, R2 = 14 ohm, L = 25 mH, i
C = 200 mF. La tensió del generador és v (t) = (50 + 80 cos (w0t) + 30 cos (2 w0t + 60 °)) V, on la freqüència fonamental és f0 = 50 Hz.
El primer pas és trobar la funció de transferència:
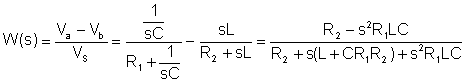
Substitució de valors numèrics en unitats V, A, ohm, mH, mF, kHz:
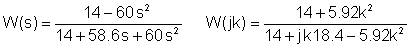
Fusió de les dues taules:
| k V Sk |  | V abk |
|---|---|---|
| 0 50 |  | 50 |
| 1 80 |  | 79.3 i-J66.3 |
| 2 30 ej60 |  | 29.7 i-J44.7 |
Finalment, la funció de temps:
vab(t) = 50 + 79.3 cos (w1t - 66.3°) + 29.7 cos (2w1t - 44.7°) [V]
i el valor rms:
English
English
German
French
Spanish
Portuguese
Russian
Chinese (Simplified)
Chinese (Traditional)
Japanese
Korean
Hungarian