 Klicken Sie auf oder tippen Sie auf die Beispielschaltkreise, um TINACloud aufzurufen und den interaktiven Gleichstrommodus auszuwählen, um sie online zu analysieren.
Klicken Sie auf oder tippen Sie auf die Beispielschaltkreise, um TINACloud aufzurufen und den interaktiven Gleichstrommodus auszuwählen, um sie online zu analysieren. Erhalten Sie einen kostengünstigen Zugang zu TINACloud, um die Beispiele zu bearbeiten oder eigene Schaltungen zu erstellen
In diesem und den folgenden Kapiteln werden wir ein sehr wichtiges Thema vorstellen: Wechselstrom oder Wechselstrom. Der Name Wechselstrom ist nicht sehr präzise und umfasst normalerweise Schaltungen mit sinusförmigen Spannungen und Strömen. Wechselstrom kann jedoch auch eine beliebige Stromwellenform bedeuten. Die Bedeutung der Wechselspannung ist, dass diese Spannung weltweit für die Hauptstromquelle in Haushalten und in der Industrie verwendet wird. Es ist auch die Basis für viele Elektronik-, Telekommunikations- und Industrieanwendungen.
Um mit sinusförmigen Wellenformen und den damit verbundenen Schaltungen umzugehen, verwenden wir eine einfache und elegante Methode, die als Zeigermethode bezeichnet wird. Zeiger basieren auf den Eigenschaften komplexer Zahlen, die ideal für die Darstellung sinusförmiger Größen sind. In diesem Kapitel werden die wichtigsten Fakten zu komplexen Zahlen und deren Operationen zusammengefasst. Wir werden auch zeigen, wie der Interpreter von TINA Berechnungen mit komplexen Zahlen vereinfacht.
Komplexe Zahlen bestehen aus zwei Teilen: a Realteil (x), das ist eine reelle Zahl und eine sogenannte Imaginärteil (y), eine reelle Zahl, multipliziert mit 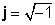
z = x + jy
woher 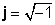
Beispiele für komplexe Zahlen:
z 1 = 1 + j
z 2 = 4-2 j
z 3 = 3- 5j
Komplexe Zahlen wurden ursprünglich im XNUMX. Jahrhundert eingeführt, um die Wurzeln von Polynomen darzustellen, die nicht allein mit reellen Zahlen dargestellt werden konnten. Zum Beispiel die Wurzeln der Gleichung x2 + 2x + 2 = 0 kann nur als beschrieben werden 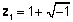
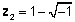
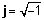
Geometrische Darstellung komplexer Zahlen
Rechteckform
Da eine komplexe Zahl immer in ihre reellen und komplexen Teile unterteilt werden kann, können wir eine komplexe Zahl als Punkt auf einer zweidimensionalen Ebene darstellen. Der Realteil einer komplexen Zahl ist die Projektion des Punktes auf die Realachse, und der Imaginärteil der Zahl ist die Projektion auf die Imaginärachse. Wenn eine komplexe Zahl als die Summe von Real- und Imaginärteilen dargestellt wird, sagen wir, dass sie in ist rechteckig or algebraische Form.
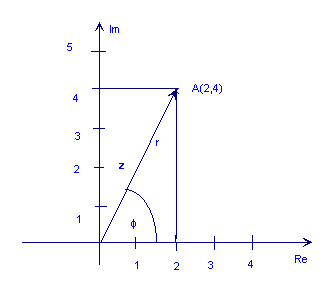
Die folgende Abbildung zeigt die komplexe Nummer z = 2 + 4j
Polare und exponentielle Form
Wie Sie aus der obigen Abbildung sehen können, könnte der Punkt A auch durch die Länge des Pfeils dargestellt werden. r (auch als absoluter Wert, Größe oder Amplitude bezeichnet) und deren Winkel (oder Phase), φ relativ gegen den Uhrzeigersinn zur positiven horizontalen Achse. Dies ist das polar Form einer komplexen Zahl. Es wird als r ∠ bezeichnet φ.
Der nächste Schritt ist sehr wichtig. Eine komplexe Zahl in Polarform kann auch geschrieben werden exponentiell bilden:
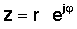
Dieser einfache Ausdruck zeichnet sich dadurch aus, dass er anstelle der üblichen reellen Zahl eine imaginäre Zahl im Exponenten hat. Dieses komplexe Exponential verhält sich ganz anders als die Exponentialfunktion mit einem echten Argument. Während ex wächst schnell in der Größe, um x> 0 zu erhöhen, und verringert sich für x <0, die Funktion 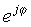
Die Euler-Formel stellt eine verbindende Verbindung zwischen den rechteckigen, polaren und exponentiellen Formen komplexer Zahlen dar:
z = x + jy = re jφ = r (cos φ + j Sünde φ )
woher 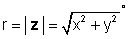
und φ = tan-1 (y / x).
Für unser Beispiel oben z = 2 + 4j:
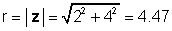
φ = tan-1 (4 / 2) = 63.4 °
deswegen 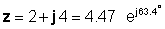
Oder umgekehrt:
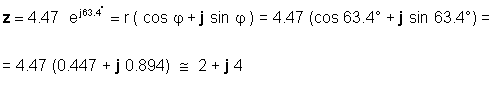
Je nach Anwendung müssen Sie mit beiden Formularen vertraut sein. Zum Beispiel ist Addition oder Subtraktion offensichtlich einfacher, wenn die Zahlen in rechteckiger Form vorliegen, während Multiplikation und Division einfacher sind, wenn die Zahlen in Exponentialform vorliegen.
Operationen mit komplexen Zahlen
Die Operationen, die mit komplexen Zahlen ausgeführt werden können, ähneln denen für reelle Zahlen. Die Regeln und einige neue Definitionen sind unten zusammengefasst.
Operationen mit j
Die Operationen mit j Folgen Sie einfach der Definition der imaginären Einheit.


Um schnell und genau arbeiten zu können, sollten Sie sich diese Regeln einprägen:
j 2 = -1
j 3 =-j
j 4 =1
1/j = -j
j2 = -1 folgt einfach aus der Definition von 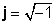
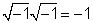
Für 1 /jmultiplizieren wir 1 /jby j / j = 1 und erhalten j/ (jj) = j / (- 1) = -j.
Komplexes Konjugat
Das komplexe Konjugat einer komplexen Zahl lässt sich leicht ableiten und ist sehr wichtig. Um das komplexe Konjugat einer komplexen Zahl in rechteckiger Form zu erhalten, ändern Sie einfach das Vorzeichen des Imaginärteils. Um dies für eine Zahl in exponentieller Form zu tun, ändern Sie das Vorzeichen des Winkels der komplexen Zahl, wobei der absolute Wert gleich bleibt.
Das komplexe Konjugat einer komplexen Zahl z wird oft mit bezeichnet z*.
Angesichts der komplexen Nummer z= a + jb ist sein komplexes Konjugat z*= a– jb.
If z wird in exponentieller Form angegeben, 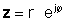
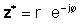
Anhand der obigen Definitionen kann man leicht erkennen, dass eine komplexe Zahl multipliziert mit ihrem komplexen Konjugat das Quadrat des absoluten Werts der komplexen Zahl ergibt:
zz* = r2 = a2 + b2
Indem Sie eine komplexe Zahl und deren Konjugat addieren oder subtrahieren, erhalten wir die folgenden Beziehungen:
z + z * = 2a
deswegen
Re (z) = a = ( z + z * ) / 2
Ähnlich:
z - z * =j2b
deswegen
Ich bin(z) = b = ( z -z * ) / 2j
Beweis:
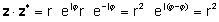
oder die Real- und Imaginärteile multiplizieren und verwenden j2= -1
zz* = (a + jb) (a - jb) = a2+a jb - a jb - jbjb = a2j2 = a2 + b2
z + z* = a + jb + a - jb = 2a
z - z*= a + jb - a + jb =j2b
Numerische Beispiele:
In rechteckiger Form:
z = 3 + j4
z* = 3– j4
zz * = 9 + 16 = 25
In polarer Form
z = 5 ≤ 53.13 °
z * = 5 ° C - 53.13 °
In exponentieller Form:
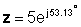
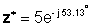
Addition und Subtraktion
Das Addieren und Subtrahieren komplexer Zahlen ist unkompliziert - wir müssen nur den Real- und den Imaginärteil getrennt addieren. Zum Beispiel wenn
z1 = 3 - 4j und z2 = 2 + 3j
dann
z1 + z2 = 3 - 4j + 2 + 3j = 3 + 2 - 4j + 3j = 5 - j
z1 - z2 = 3 - 4j - 2 - 3j = 3 - 2 - 4j - 3j = 1 - j7
Natürlich sollten wir für diese Operationen die rechteckige Form verwenden. Wenn die Zahlen in exponentieller oder polarer Form angegeben werden, sollten wir sie zuerst in die rechteckige Form umwandeln, indem wir die Euler-Formel verwenden, wie zuvor angegeben.
Vervielfältigen
Es gibt zwei Methoden zur Multiplikation komplexer Zahlen:
Multiplikation komplexer Zahlen in rechteckiger Form
Um die Operation auszuführen, multiplizieren Sie einfach den Real- und Imaginärteil einer Zahl nacheinander mit dem Real- und Imaginärteil der anderen Zahl und verwenden Sie die Identität j2 = -1.
z1z2 = (a1 + jb1) (ein2 + jb2) = a1 a2 + jb1a2+ jb2a1 - b1b2 = a1 a2- b1b2 + j(b1a2+ jb2a1)
Wenn die komplexen Zahlen numerisch angegeben werden, muss die obige Formel nicht verwendet werden. Zum Beispiel lassen
z1 = 3 - 4j und z2 = 2 + 3j
Bei direkter Multiplikation der Komponenten:
z1z2 = (3 - 4j) (2 + 3j) = 6-8j +9j + 12 = 18 + j
oder mit der Formel: z1z2 = a1 a2- b1b2 + j(b1a2+ B2a1)
z1z2 = 6 + 12 + j (-8 + 9) = 18 + j
Wir glauben, dass Sie eher einen Fehler machen, wenn Sie die Formel verwenden, als wenn Sie die Komponenten direkt multiplizieren.
z1: = 3-4 * j
z2: = 2 + 3 * j
z1 * z2 = [18 + 1 * j]
Mathe als m importieren
cmath als c importieren
z1=komplex('3-4j')
z2=komplex('2+3j')
print(“z1*z2=",z1*z2)
Multiplikation komplexer Zahlen in polarer oder exponentieller Form
Multiplizieren Sie dazu die Absolutwerte und addieren Sie die Winkel der beiden komplexen Zahlen. Lassen:
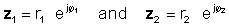
Dann mit der Regel der Multiplikation von Exponentialfunktionen:
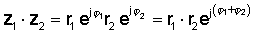
oder in polarer Form
z1 z2 = r1 r2 ∠φ1 + φ2
Hinweis: Wir haben diese Regel bereits bei der Berechnung verwendet zz *über. Da der Winkel des Konjugats das entgegengesetzte Vorzeichen des ursprünglichen Winkels hat, ist eine komplexe Zahl multipliziert mit ihrem eigenen Konjugat immer eine reelle Zahl; nämlich das Quadrat seines absoluten Wertes: zz * = r2
Zum Beispiel lassen Sie:
z1 = 5 ≤ 30 ° und z2 = 4 ∠ -60 °
dann
z1z2 = 20 ∠ -30 °
oder in exponentieller Form
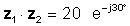
Die Multiplikation ist offensichtlich einfacher, wenn die Zahlen polar oder exponentiell sind.
Wenn die komplexen Zahlen jedoch in rechteckiger Form angegeben werden, sollten Sie die Multiplikation direkt wie oben gezeigt durchführen, da es zusätzliche Schritte gibt, wenn Sie die Zahlen vor dem Multiplizieren in polare Form konvertieren. Ein weiterer zu berücksichtigender Faktor ist, ob die Antworten in rechteckiger Form oder in polarer / exponentieller Form vorliegen sollen. Wenn die beiden Zahlen beispielsweise rechteckig sind, Sie jedoch möchten, dass ihr Produkt in polarer Form vorliegt, ist es sinnvoll, sie sofort zu konvertieren und dann zu multiplizieren.
Division
Es gibt zwei Methoden zur Division komplexer Zahlen:
Division komplexer Zahlen in rechteckiger Form
Um die Operation auszuführen, multiplizieren Sie den Zähler und den Nenner mit dem Konjugat des Nenners. Der Nenner wird zu einer reellen Zahl und die Division reduziert sich auf die Multiplikation zweier komplexer Zahlen und eine Division durch eine reelle Zahl, das Quadrat des Absolutwerts des Nenners.
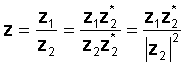
Zum Beispiel lassen Sie:
z1 = 3 - 4j und z2 = 2 + 3j
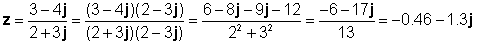
Lassen Sie uns dieses Ergebnis mit dem Interpreter von TINA überprüfen:
z1: = 3-4 * j
z2: = 2 + 3 * j
z1 / z2 = [- 461.5385m-1.3077 * j]
Mathe als m importieren
cmath als c importieren
z1=komplex('3-4j')
z2=komplex('2+3j')
print(“z1/z2=",z1/z2)
Division komplexer Zahlen in polarer oder exponentieller Form
Um die Operation auszuführen, dividieren Sie die Absolutwerte (Beträge) und subtrahieren Sie den Winkel des Nenners vom Winkel des Zählers. Lassen:
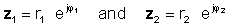
dann mit der Regel der Aufteilung der Exponentialfunktionen
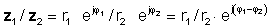
oder in polarer Form
z 1 / z2 = r1 / r2 ∠ φ 1- φ 2
Zum Beispiel lassen Sie:
z 1 = 5 ∠ 30 ° und z 2 = 2 60 -XNUMX °
dann
z 1 / z2 = 2.5 ≤ 90 °
oder in exponentiellen und rechteckigen Formen
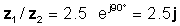
Lassen Sie uns dieses Ergebnis mit dem Interpreter von TINA überprüfen:
z1: = 5 * exp (j * degtorad (30))
z2: = 2 * exp (j * degtorad (-60))
z1 / z2 = [0 + 2.5 * j]
Mathe als m importieren
cmath als c importieren
z1=5*(c.exp(complex(0,m.radians(30))))
z2=2*(c.exp(complex(0,m.radians(-60))))
print(“z1/z2=",z1/z2)
Die Division ist offensichtlich einfacher, wenn die Zahlen in polarer oder exponentieller Form vorliegen.
Wenn die komplexen Zahlen jedoch in rechteckiger Form angegeben werden, sollten Sie in Betracht ziehen, die Division direkt mit der oben gezeigten komplexen konjugierten Methode durchzuführen, da es zusätzliche Schritte gibt, wenn Sie die Zahlen vor dem Teilen in polare Form konvertieren. Ein weiterer zu berücksichtigender Faktor ist, ob die Antworten in rechteckiger Form oder in polarer / exponentieller Form vorliegen sollen. Wenn die beiden Zahlen beispielsweise rechteckig sind, Sie jedoch ihren Quotienten in polarer Form wünschen, ist es sinnvoll, sie sofort zu konvertieren und dann zu teilen.
Lassen Sie uns nun die Verwendung komplexer Zahlen durch numerischere Probleme veranschaulichen. Wie gewohnt werden wir unsere Lösungen mit dem TINA Interpreter überprüfen. Der Interpreter arbeitet mit Bogenmaß, verfügt jedoch über Standardfunktionen für die Umrechnung von Bogenmaß in Grad oder umgekehrt.
Beispiel 1 Finden Sie die polare Darstellung:
z = 12 - j 48
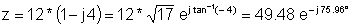
z: = 12-j * 48;
abs (z) = [49.4773]
Bogen (z) = [- 1.3258]
Radtodeg (Bogen (z)) = [- 75.9638]
Mathe als m importieren
cmath als c importieren
z=12-komplex(48j)
print(“abs(z)=",abs(z))
print(“arc(z)=",c.phase(z))
print(“degrees(arc(z))=”,m.degrees(c.phase(z)))
Beispiel 2 Finden Sie die rechteckige Darstellung:
z = 25 e j 125 °
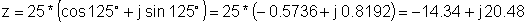
z: = 25 * exp (j * (degtorad (125)));
z = [- 14.3394 + 20.4788 * j]
Re (z) = [- 14.3394]
Im (z) = [20.4788]
Mathe als m importieren
cmath als c importieren
z=25*c.exp(complex(0,m.radians(125)))
print(“z=",z)
print(“real(z)=",z.real)
print(“imag(z)=",z.imag)
Beispiel 3 Finden Sie die polare Darstellung der folgenden komplexen Zahlen:
z 1 = 12 + j 48 z2 = 12 - j48 z3= -12 + j 48 z4= -12 - j 48
Die absoluten Werte aller vier Zahlen sind gleich, da der absolute Wert unabhängig von den Vorzeichen ist. Nur die Winkel sind unterschiedlich.
z1: = 12 + j * 48;
abs (z1) = [49.4773]
Bogen (z1) = [1.3258]
radtodeg (arc (z1)) = [75.9638]
z2: = 12-j * 48;
abs (z2) = [49.4773]
Bogen (z2) = [- 1.3258]
radtodeg (arc (z2)) = [- 75.9638]
z3: = - 12 + j * 48;
abs (z3) = [49.4773]
Bogen (z3) = [1.8158]
radtodeg (arc (z3)) = [104.0362]
z4: = - 12-j * 48:
abs (z4) = [49.4773]
Bogen (z4) = [- 1.8158]
radtodeg (arc (z4)) = [- 104.0362]
Mathe als m importieren
cmath als c importieren
z1=komplex('12+48j')
print(“abs(z1)=",abs(z1))
print(“arc(z1)=",c.phase(z1))
print(“degrees(arc(z1))=”,m.degrees(c.phase(z1)))
z2=komplex('12-48j')
print(“abs(z2)=",abs(z2))
print(“arc(z2)=",c.phase(z2))
print(“degrees(arc(z2))=”,m.degrees(c.phase(z2)))
z3=komplex('-12+48j')
print(“abs(z3)=",abs(z3))
print(“arc(z3)=",c.phase(z3))
print(“degrees(arc(z3))=”,m.degrees(c.phase(z3)))
z4=komplex('-12-48j')
print(“abs(z4)=",abs(z4))
print(“arc(z4)=",c.phase(z4))
print(“degrees(arc(z4))=”,m.degrees(c.phase(z4)))
Die arc () -Funktion von TINA bestimmt den Winkel einer komplexen Zahl und platziert sie automatisch korrekt in einem der vier Quadranten.
Seien Sie jedoch vorsichtig mit der Bräune-1 Funktion zum Ermitteln des Winkels, da er nur im ersten und vierten Quadranten (–90 °) auf Rückgabewinkel beschränkt istφ<90 °).
Da z1 Befindet sich im ersten Quadranten des Koordinatensystems, so lautet die Berechnung:
α 1 = tan-1(48 / 12) = tan-1(4) = 75.96 °
Da z4 befindet sich im dritten Quadranten des Koordinatensystems, tan-1gibt den Winkel nicht korrekt zurück. Die Winkelberechnung lautet:
α 4 = 180 ° + 75.96 ° = 255.96 ° oder -360 ° + 255.96 ° = - 104.04 °, was der von TINA berechneten entspricht.
z2 liegt im vierten Quadranten des Koordinatensystems Die Winkelberechnung lautet:
α 2 = tan-1(-48 / 12) = tan-1(-4) = -75.96 °
z3, Befindet sich jedoch im 2-Quadranten des Koordinatensystems, so ist tan-1 gibt den Winkel nicht richtig zurück. Die Winkelberechnung lautet:
α 3 = 180 ° -75.96 ° = 104.04 °.
Beispiel 4 Wir haben zwei komplexe Zahlen: z1= 4 - j 6 und z2 = 5 ej45 ° .
Finden Sie z3 = z1 + z2; z4 = z1 - z2; z5 = z1 * z2; z6 = z1 / z2
Zuerst lösen wir das Problem mit dem TINA Interpreter
{Lösung durch den TINA-Dolmetscher} |
Beachten Sie, wie TINA mühelos mit den beiden komplexen Zahlen umgeht, die in unterschiedlichen Formen angegeben werden.
Die Lösung ist ohne den Dolmetscher komplizierter. Damit wir die verschiedenen Multiplikations- und Divisionsmethoden vergleichen können, werden wir zunächst die polare Form von bestimmen z1 und die rechteckige Form von z2 .
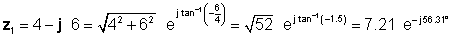
Als nächstes finden wir die vier Lösungen mit den einfachsten Formen zuerst: rechteckig für Addition und Subtraktion und exponentiell für Multiplikation und Division:
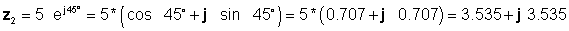
z 3 = z1 + z2 = 4 - j 6 + 3.535 + j 3.535 = 7.535 - j2.465
z 4 = z1 - z2 = 4 - j 6 - 3.535 - j 3.535 = 0.465 - j9.535
z 5 = z1 * z2 = 7.21 * 5 * ej(-56.31 ° + 45 °) = 36.05 e -j11.31 ° = 36.03 * (cos (-11.31 °) +j* sin (-11.31 °))
z 5 = 35.33 - j 7.07
z 6 = z1/z2= (7.21 / 5) * e j (-56.31 ° -45 °) = 1.442 e - j 101.31 ° = 1.442 (cos (-101.31 °) +j* sin (-101.31 °))
z 6 = -0.2828 - j 1.414
die mit den mit dem TINA Interpreter erzielten Ergebnissen übereinstimmen.
Die Multiplikation erfolgt in rechteckiger Form:
z 5 =z1*z2 = (4-j6) * 3.535 * (1 +j) = 7.07 * (2-j3) * (1 +j) = 7.07 * (2-j3+j2 + 3) = 7.07 * (5-j) = 35.35-j7.07
Schließlich die Aufteilung in rechteckiger Form durchgeführt:
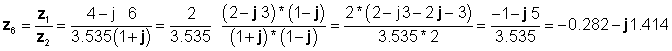
die mit den vorherigen Ergebnissen übereinstimmen.

