Klicken Sie auf oder tippen Sie auf die Beispielschaltkreise, um TINACloud aufzurufen und den interaktiven Gleichstrommodus auszuwählen, um sie online zu analysieren.
Klicken Sie auf oder tippen Sie auf die Beispielschaltkreise, um TINACloud aufzurufen und den interaktiven Gleichstrommodus auszuwählen, um sie online zu analysieren. Erhalten Sie einen kostengünstigen Zugang zu TINACloud, um die Beispiele zu bearbeiten oder eigene Schaltungen zu erstellen
Wie wir bereits gesehen haben, können Schaltungen mit sinusförmiger Erregung mit gelöst werden komplexe Impedanzen für die Elemente und komplexer Peak or Komplex Effektivwerte für die Ströme und Spannungen. Unter Verwendung der Version der Kirchhoffschen Gesetze mit komplexen Werten können Knoten- und Netzanalysetechniken verwendet werden, um Wechselstromkreise auf ähnliche Weise wie Gleichstromkreise zu lösen. In diesem Kapitel werden wir dies anhand von Beispielen für Kirchhoffs Gesetze zeigen.
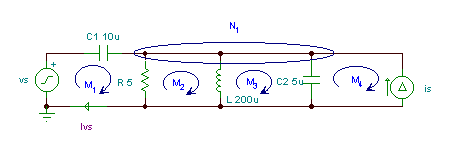
Beispiel 1
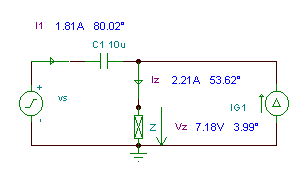
Finden Sie die Amplitude und den Phasenwinkel des Stroms ivs(T) if
vS(t) = VSM cos 2pft; i (t) = ichSM cos 2pft; VSM = 10 V; ichSM = 1 A; f = 10 kHz;
Insgesamt haben wir 10 unbekannte Spannungen und Ströme, nämlich: i, iC1,R,L,C2, vC1, vR, vL, vC2 und vIS. (Wenn wir komplexe Spitzen- oder Effektivwerte für die Spannungen und Ströme verwenden, haben wir insgesamt 20 reelle Gleichungen!)
Die Gleichungen:
Schleifen- oder Maschengleichungen: z M1 - VSM +VC1M+VRM = 0
M2 - VRM + VLM = 0
M3 - VLM + VC2M = 0
M4 - VC2M + VIsM = 0
Ohmsche Gesetze VRM = R *IRM
VLM = j*w* L *ILM
IC1M = j*w*C1*VC1M
IC2M = j*w*C2*VC2M
Knotengleichung für N1 - IC1M - ISM + IRM + ILM +IC2M = 0
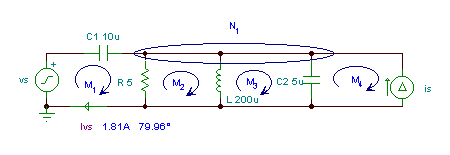
für Serienelemente I = IC1MWenn Sie das Gleichungssystem lösen, können Sie den unbekannten Strom finden:
ivs (t) = 1.81 cos (wt + 79.96°) A
Das Lösen eines so großen Systems komplexer Gleichungen ist sehr kompliziert, daher haben wir es nicht im Detail gezeigt. Jede komplexe Gleichung führt zu zwei reellen Gleichungen, daher zeigen wir die Lösung nur anhand der mit dem TINA-Interpreter berechneten Werte.
Die Lösung mit dem TINA Interpreter:
om: = 20000 * pi;
Vs: = 10;
Is: = 1;
SysIc1, Ir, IL, Ic2, Vc1, Vr, VL, Vc2, Vis, Ivs
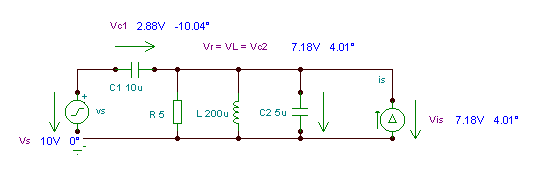
Vs=Vc1+Vr {M1}
Vr=VL {M2}
Vr=Vc2 {M3}
Vc2=Vis {M4}
Ivs=Ir+IL+Ic2-Is {N1}
{Ohmsche Regeln}
Ic1 = j * om * C1 * Vc1
Vr = R * Ir
VL = j * om * L * IL
Ic2 = j * om * C2 * Vc2
Ivs = Ic1
end;
Ivs = [3.1531E-1 + 1.7812E0 * j]
abs (Ivs) = [1.8089]
fiIvs: = 180 * arc (Ivs) / pi
fiIvs = [79.9613]
sympy als s importieren
cmath als c importieren
cp= lambda Z : „{:.4f}“.format(Z)
om=20000*c.pi
Vs=10
Ist=1
Ic1,Ir,IL,Ic2,Vc1,Vr,VL,Vc2,Vis,Ivs=s.symbols('Ic1 Ir IL Ic2 Vc1 Vr VL Vc2 Vis Ivs')
A=[s.Eq(Vc1+Vr,Vs),s.Eq(VL,Vr),s.Eq(Vc2,Vr),s.Eq(Vis,Vc2), #M1, M2, M3, M4
s.Gl(Ir+IL+Ic2-Is,Ivs), #N1
s.Eq(1j*om*C1*Vc1,Ic1),s.Eq(R*Ir,Vr),s.Eq(1j*om*L*IL,VL),s.Eq(1j*om*C2*Vc2,Ic2),s.Eq(Ic1,Ivs)] #Ohm’s rules
Ic1,Ir,IL,Ic2,Vc1,Vr,VL,Vc2,Vis,Ivs=[complex(Z) for Z in tuple(s.linsolve(A,(Ic1,Ir,IL,Ic2,Vc1,Vr,VL,Vc2,Vis,Ivs)))[0]]
drucken(Ivs)
print(“abs(Ivs)=",cp(abs(Ivs)))
print(“180*c.phase(Ivs)/c.pi=",cp(180*c.phase(Ivs)/c.pi))
Die Lösung mit TINA:
Um dieses Problem von Hand zu lösen, arbeiten Sie mit den komplexen Impedanzen. Zum Beispiel R, L und C.2 sind parallel geschaltet, sodass Sie die Schaltung vereinfachen können, indem Sie ihr paralleles Äquivalent berechnen. || bedeutet das parallele Äquivalent der Impedanzen:
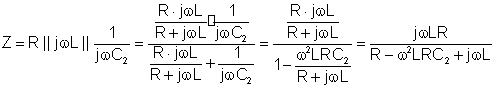
Numerisch:
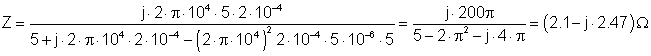
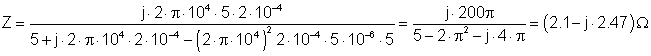
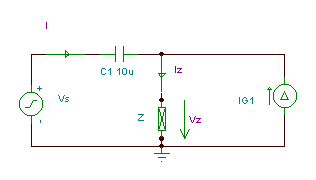
Die vereinfachte Schaltung mit der Impedanz:
Die Gleichungen in geordneter Form: I + IG1 = IZ
VS = VC1 +VZ
VZ = Z · IZ
I = j w C1· VC1
Es gibt vier Unbekannte. I; IZ; VC1; VZ - und wir haben vier Gleichungen, so dass eine Lösung möglich ist.
Express I nach dem Ersetzen der anderen Unbekannten aus den Gleichungen:
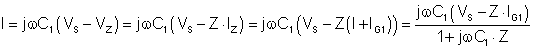
Numerisch
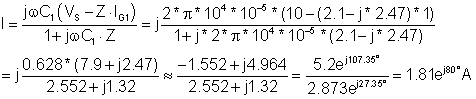
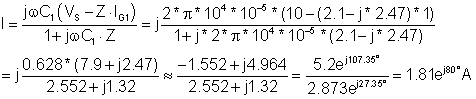
Nach dem Ergebnis des Dolmetschers von TINA.
om: = 20000 * pi;
Vs: = 10;
Is: = 1;
Z: = Replus (R, Replus (j * om * L, 1 / j / om / C2));
Z = [2.1046E0-2.4685E0 * j]
sys ich
I = j * om * C1 * (Vs-Z * (I + Is))
end;
I = [3.1531E-1 + 1.7812E0 * j]
abs (I) = [1.8089]
180 * Bogen (I) / pi = [79.9613]
sympy als s importieren
cmath als c importieren
Replus= Lambda R1, R2 : R1*R2/(R1+R2)
om=20000*c.pi
Vs=10
Ist=1
Z=Replus(R,Replus(1j*om*L,1/1j/om/C2))
print('Z=',cp(Z))
I=s.symbols('I')
A=[s.Eq(1j*om*C1*(Vs-Z*(I+Is)),I),]
I=[complex(Z) für Z in tuple(s.linsolve(A,I))[0]][0]
print(“I=",cp(I))
print(“abs(I)=",cp(abs(I)))
print(“180*c.phase(I)/c.pi=",cp(180*c.phase(I)/c.pi))
Die Zeitfunktion des Stroms ist also:
i (t) = 1.81 cos (wt + 80°) A
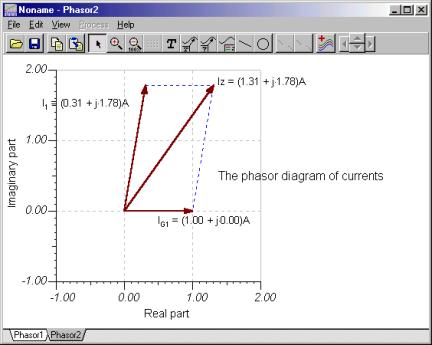
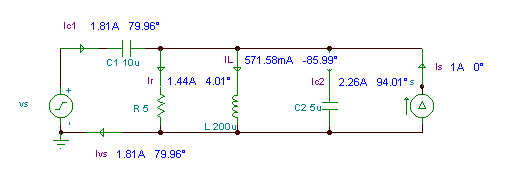
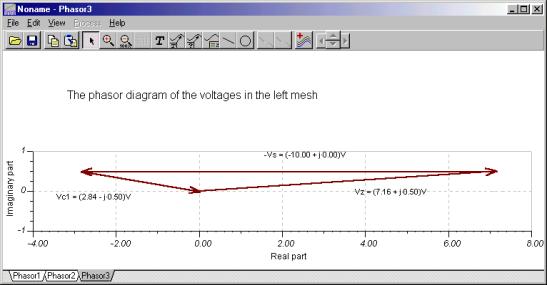
Sie können die aktuelle Regel von Kirchhoff anhand von Zeigerdiagrammen überprüfen. Das folgende Bild wurde durch Überprüfen der Knotengleichung in i entwickeltZ = i + iG1 bilden. Das erste Diagramm zeigt die durch die Parallelogrammregel hinzugefügten Zeiger, das zweite zeigt die Dreiecksregel der Zeigeraddition.
Lassen Sie uns nun KVR mithilfe der Zeigerdiagrammfunktion von TINA demonstrieren. Da die Quellenspannung in der Gleichung negativ ist, haben wir das Voltmeter „rückwärts“ angeschlossen. Das Zeigerdiagramm zeigt die ursprüngliche Form der Kirchhoffschen Spannungsregel.
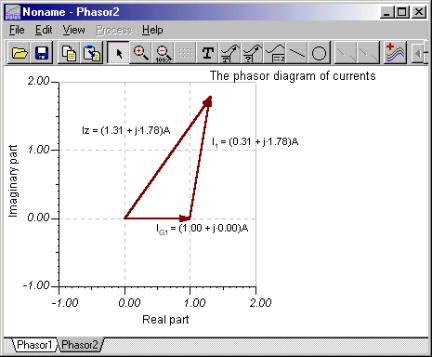
Das erste Zeigerdiagramm verwendet die Parallelogrammregel, während das zweite die Dreiecksregel verwendet.
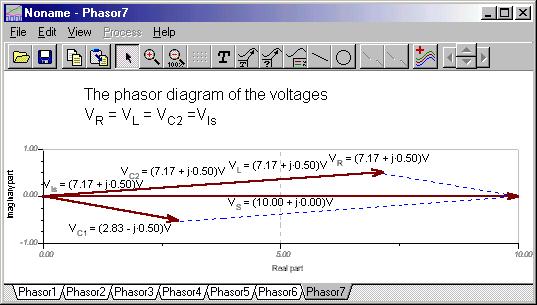
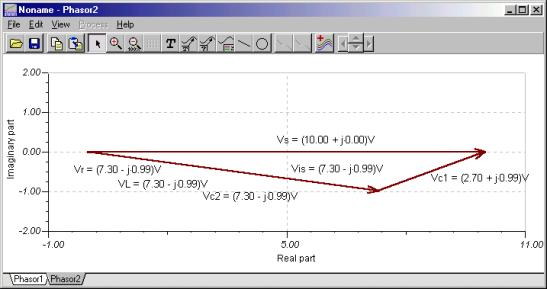
Zur Veranschaulichung von KVR in der Form V.C1 + VZ - VS = 0, wir haben das Voltmeter wieder rückwärts an die Spannungsquelle angeschlossen. Sie können sehen, dass das Zeigerdreieck geschlossen ist.
Beispiel 2
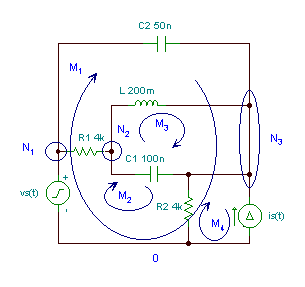
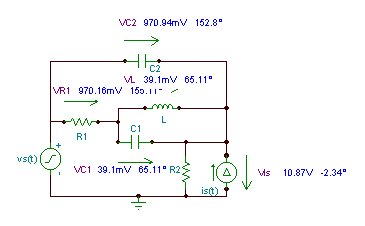
Finden Sie die Spannungen und Ströme aller Komponenten, wenn:
vS(t) = 10 cos wFernseher, iS(t) = 5 cos (w t + 30 °) mA;
C1 = 100 nF, C2 = 50 nF, R1 = R2 = 4 k; L = 0.2 H f = 10 kHz.
Die Unbekannten seien die komplexen Spitzenwerte der Spannungen und Ströme von "passiven" Elementen sowie der Strom der Spannungsquelle (iVS ) und die Spannung der Stromquelle (vIS ). Insgesamt gibt es zwölf komplexe Unbekannte. Wir haben drei unabhängige Knoten, vier unabhängige Schleifen (markiert als M.I) und fünf passive Elemente, die durch fünf „Ohmsche Gesetze“ charakterisiert werden können - insgesamt gibt es 3 + 4 + 5 = 12 Gleichungen:
Knotengleichungen für N1 IVsM = IchR1M + IC2M
für N2 IR1M = IchLM + IC1M
für N3 IC2M + ILM + IC1M +IsM = IchR2M
Schleifengleichungen bilden1 VSM = VC2M + VR2M
bilden2 VSM = VC1M + VR1M+ VR2M
bilden3 VLM = VC1M
bilden4 VR2M = VIsM
Ohmsche Gesetze VR1M = R1*IR1M
VR2M = R2*IR2M
IC1m = j *w*C1*VC1M
IC2m = j *w*C2*VC2M
VLM = j *w* L * ILM
Vergessen Sie nicht, dass jede komplexe Gleichung zu zwei reellen Gleichungen führen kann. Kirchhoffs Methode erfordert daher viele Berechnungen. Es ist viel einfacher, die Zeitfunktionen der Spannungen und Ströme unter Verwendung eines Differentialgleichungssystems (hier nicht erörtert) zu lösen. Zuerst zeigen wir die vom TINA Interpreter berechneten Ergebnisse:
f: = 10000;
Vs: = 10;
s: = 0.005 * exp (j * pi / 6);
om: = 2 * pi * f;
sys ir1, ir2, ic1, ic2, iL, vr1, vr2, vc1, vc2, vL, vis, ivs
ivs=ir1+ic2 {1}
ir1=iL+ic1 {2}
ic2+iL+ic1+Is=ir2 {3}
Vs=vc2+vr2 {4}
Vs=vr1+vr2+vc1 {5}
vc1=vL {6}
vr2=vis {7}
vr1=ir1*R1 {8}
vr2=ir2*R2 {9}
ic1=j*om*C1*vc1 {10}
ic2=j*om*C2*vc2 {11}
vL=j*om*L*iL {12}
end;
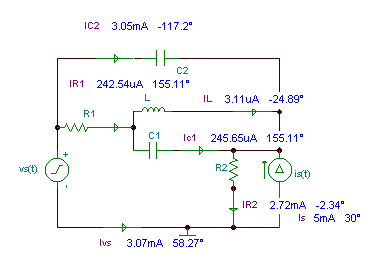
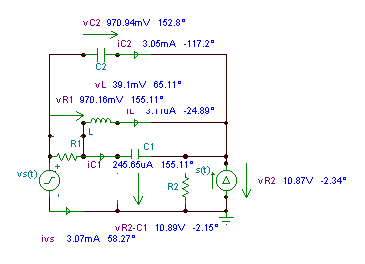
abs (vr1) = [970.1563m]
abs (vr2) = [10.8726]
abs (ic1) = [245.6503u]
abs (ic2) = [3.0503m]
abs (vc1) = [39.0965m]
abs (vc2) = [970.9437m]
abs (iL) = [3.1112u]
abs (vL) = [39.0965m]
abs (ivs) = [3.0697m]
180 + radtodeg (Bogen (ivs)) = [58.2734]
abs (vis) = [10.8726]
radtodeg (arc (vis)) = [- 2.3393]
radtodeg (arc (vr1)) = [155.1092]
radtodeg (arc (vr2)) = [- 2.3393]
radtodeg (arc (ic1)) = [155.1092]
radtodeg (arc (ic2)) = [- 117.1985]
radtodeg (arc (vc2)) = [152.8015]
radtodeg (arc (vc1)) = [65.1092]
Radtodeg (Bogen (iL)) = [- 24.8908]
Radtodeg (Bogen (vL)) = [65.1092]
sympy als s importieren
Mathe als m importieren
cmath als c importieren
cp= lambda Z : „{:.4f}“.format(Z)
f = 10000
Vs=10
S=0.005*c.exp(1j*c.pi/6)
om=2*c.pi*f
ir1,ir2,ic1,ic2,iL,vr1,vr2,vc1,vc2,vL,vis,ivs=s.symbols('ir1 ir2 ic1 ic2 iL vr1 vr2 vc1 vc2 vL vis ivs')
A=[s.Gl(ir1+ic2,ivs), #1
s.Eq(iL+ic1,ir1), #2
s.Eq(ic2+iL+ic1+Is,ir2), #3
s.Eq(vc2+vr2,Vs), #4
s.Eq(vr1+vr2+vc1,Vs), #5
s.Eq(vL,vc1), #6
s.Gl(vis,vr2), #7
s.Eq(ir1*R1,vr1), #8
s.Eq(ir2*R2,vr2), #9
s.Eq(1j*om*C1*vc1,ic1), #10
s.Eq(1j*om*C2*vc2,ic2), #11
s.Eq(1j*om*L*iL,vL)] #12
ir1,ir2,ic1,ic2,iL,vr1,vr2,vc1,vc2,vL,vis,ivs=[complex(Z) for Z in tuple(s.linsolve(A,(ir1,ir2,ic1,ic2,iL,vr1,vr2,vc1,vc2,vL,vis,ivs)))[0]]
print(“abs(vr1)=",cp(abs(vr1)))
print(“abs(vr2)=",cp(abs(vr2)))
print(“abs(ic1)=",cp(abs(ic1)))
print(“abs(ic2)=",cp(abs(ic2)))
print(“abs(vc1)=",cp(abs(vc1)))
print(“abs(vc2)=",cp(abs(vc2)))
print(“abs(iL)=",cp(abs(iL)))
print(“abs(vL)=",cp(abs(vL)))
print(“abs(ivs)=",cp(abs(ivs)))
print(“180+Grad(Phase(ivs))=”,cp(180+m.Grad(c.Phase(ivs))))
print(“abs(vis)=",cp(abs(vis)))
print(“degrees(phase(vis))=”,cp(m.degrees(c.phase(vis))))
print(“degrees(phase(vr1))=”,cp(m.degrees(c.phase(vr1))))
print(“degrees(phase(vr2))=”,cp(m.degrees(c.phase(vr2))))
print(“degrees(phase(ic1))=”,cp(m.degrees(c.phase(ic1))))
print(“degrees(phase(ic2))=”,cp(m.degrees(c.phase(ic2))))
print(“degrees(phase(vc2))=”,cp(m.degrees(c.phase(vc2))))
print(“degrees(phase(vc1))=”,cp(m.degrees(c.phase(vc1))))
print(“degrees(phase(iL))=”,cp(m.degrees(c.phase(iL))))
print(“degrees(phase(vL))=”,cp(m.degrees(c.phase(vL))))
Versuchen Sie nun, die Gleichungen von Hand durch Substitution zu vereinfachen. Erster Ersatz Gl. 9. in Gleichung 5.
VS = VC2 + R2 IR2 ein.)
dann Äq.8 und Äq.9. in eq 5.
VS = VC1 + R2 IR2 + R1 IR1 b.)
dann Gl. 12., Gl. 10. und ichL aus Gl. 2 in Äq.6.
VC1 = VL = jwLIL = jwL (IR1 - IchC1) = jwLIR1 - jwL jwC1 VC1
Express VC1
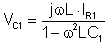
Express VC2 aus Gl. 4. und Gl. 5. und ersetze Gleichung 8, Gleichung 11. und V.C1:
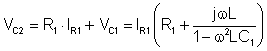
Ersetzen Sie Gleichung 2., 10., 11. und d.) In Gleichung 3. und drücke ich ausR2
IR2 = IchC2 + IR1 + IS = jwC2 VC2 + IR1 + IS
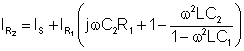
Setzen Sie nun d.) Und e.) In Gleichung 4 ein und drücken Sie I ausR1
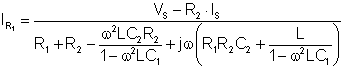
Numerisch:
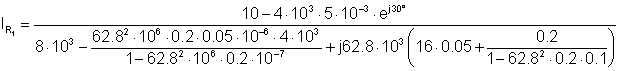
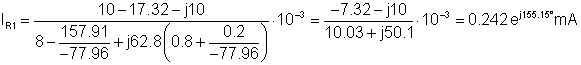
Die Zeitfunktion von iR1 ist das Folgende:
iR1(t) = 0.242 cos (wt + 155.5°) mA
Die gemessenen Spannungen: