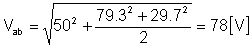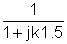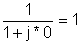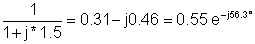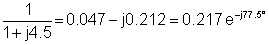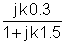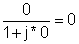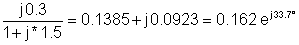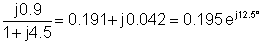Klicken Sie auf oder tippen Sie auf die Beispielschaltkreise, um TINACloud aufzurufen und den interaktiven Gleichstrommodus auszuwählen, um sie online zu analysieren.
Erhalten Sie einen kostengünstigen Zugang zu TINACloud, um die Beispiele zu bearbeiten oder eigene Schaltungen zu erstellen

Das Fourier-Theorem besagt, dass jede periodische Wellenform durch Hinzufügen entsprechend gewichteter Sinus- und Kosinusterme verschiedener Frequenzen synthetisiert werden kann. Der Satz wird in anderen Lehrbüchern ausführlich behandelt, daher werden wir nur die Ergebnisse zusammenfassen und einige Beispiele zeigen.

Unsere periodische Funktion sei f (t) = f (t ±nT), wobei T die Zeit einer Periode und n eine ganze Zahl ist.

w₀= 2p/ T die Grundkreisfrequenz.

Durch die Fourier-Satz, Die periodische Funktion kann als folgende Summe geschrieben werden:

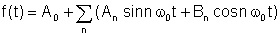
woher

A_n und B_n sind die Fourierkoeffizienten und die Summe ist das die Fourierreihe.

Eine andere Form, wahrscheinlich etwas praktischer:

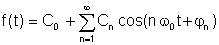
woher

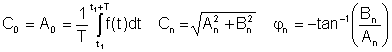
A₀ = C₀ ist der DC oder Durchschnittswert A₁, B₁ und C₁ sind die Grundkomponenten und die anderen sind die harmonischen Terme.

Während zur Approximation einiger Wellenformen möglicherweise nur wenige Terme erforderlich sind, sind für andere viele Terme erforderlich.

Im Allgemeinen gilt: Je mehr Terme enthalten sind, desto besser ist die Näherung, aber bei Wellenformen, die Stufen enthalten, wie z. B. Rechteckimpulse, ist die Gibbs-Phänomen kommt ins Spiel. Mit zunehmender Anzahl der Begriffe konzentriert sich die Überschwingung auf einen immer kleineren Zeitraum.

An gleiche Funktion f(t) = f(-t) (Achsensymmetrie) erfordert nur Kosinusterme.

An komische Funktion f(t) = – f(-t) (Punktsymmetrie) erfordert nur Sinusterme.

Eine Wellenform mit Spiegel- oder Halbwellensymmetrie hat nur ungerade Harmonische in ihrer Fourier-Darstellung.

Wir werden uns hier nicht mit der Fourier-Reihenentwicklung befassen, sondern nur eine gegebene Summe von Sinus- und Cosinuswerten als Anregung für eine Schaltung verwenden.

In den früheren Kapiteln dieses Buches haben wir uns mit sinusförmiger Erregung befasst. Wenn die Schaltung linear ist, ist die Überlagerungssatz ist gültig. Für ein Netzwerk mit nichtsinusförmiger periodischer Anregung ermöglicht uns die Überlagerung Berechnen Sie die Ströme und Spannungen für jeden Fourier-Sinus-Term nacheinander. Wenn alles berechnet ist, fassen wir schließlich die harmonischen Komponenten der Antwort zusammen.

Es ist etwas kompliziert, die verschiedenen Terme der periodischen Spannungen und Ströme zu bestimmen, und tatsächlich kann es zu einer Informationsüberflutung kommen. In der Praxis möchten wir einfach Messungen durchführen. Wir können die verschiedenen harmonischen Terme mit a messen harmonischer Analysator, Spektrumanalysator, Wellenanalysator oder Fourier-Analysator. All dies sind kompliziert und liefern wahrscheinlich mehr Daten als nötig. Manchmal reicht es aus, ein periodisches Signal nur durch seine Durchschnittswerte zu beschreiben. Es gibt jedoch verschiedene Arten von Durchschnittsmessungen.

DURCHSCHNITTLICH WERTE

Einfacher Durchschnitt or DC Der Begriff wurde in der Fourier-Darstellung als A gesehen₀

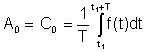
Dieser Durchschnitt kann mit Instrumenten wie dem Deprez gemessen werden Gleichstrominstrumente.

Effektiver Wert or rms (Root Mean Square) hat die folgende Definition:

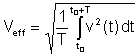
Dies ist der wichtigste Durchschnittswert, da die in Widerständen abgegebene Wärme proportional zum Effektivwert ist. Viele digitale und einige analoge Voltmeter können den Effektivwert von Spannungen und Strömen messen.

Absoluter Durchschnitt

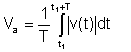
Dieser Durchschnitt ist nicht mehr wichtig; Frühere Instrumente haben diese Form des Durchschnitts gemessen.

Wenn wir die Fourier-Darstellung einer Spannungs- oder Stromwellenform kennen, können wir die Durchschnittswerte auch wie folgt berechnen:

Einfacher Durchschnitt or DC Der Begriff wurde in der Fourier-Darstellung als A gesehen₀ = C₀

Effektiver Wert or rms (quadratischer Mittelwert) ist nach Integration der Fourier-Reihe der Spannung:

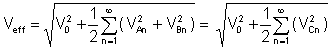
Das Klirrfaktor ist ein sehr wichtiges Verhältnis der Durchschnittswerte:

Es ist das Verhältnis des Effektivwerts der höheren harmonischen Terme zum Effektivwert der Grundschwingung:

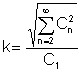
Hier scheint ein Widerspruch zu bestehen – wir lösen Netzwerke anhand harmonischer Komponenten, messen aber Durchschnittsgrößen.

Lassen Sie uns die Methode anhand einfacher Beispiele veranschaulichen:

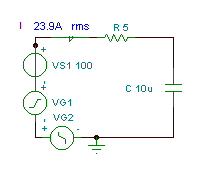
Beispiel 1

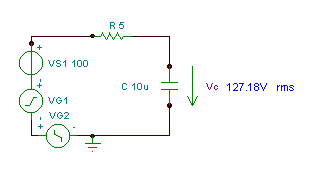
Finden Sie die Zeitfunktion und den Effektivwert (Effektivwert) der Spannung v_C(T)

wenn R = 5 Ohm, C = 10 mF und v (t) = (100 + 200 cos (w₀t) + 30 cos (3 w₀t - 90 °)) V, wobei die Grundwinkelfrequenz ist w₀= 30 krad / s.

Versuchen Sie, das Problem mit dem Superpositionssatz zu lösen.

Der erste Schritt besteht darin, die Übertragungsfunktion als Funktion der Frequenz zu ermitteln. Verwenden Sie der Einfachheit halber die Substitution: s = j w

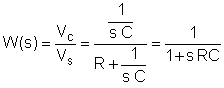
Ersetzen Sie nun die Komponentenwerte und s = jk w₀wobei k = 0; 1; 3 in diesem Beispiel und w₀= 30 Krad/s. In V, A, Ohm, mF- und Mrad / s-Einheiten:

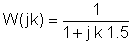
Es ist hilfreich, eine Tabelle zu verwenden, um die Schritte der numerischen Lösung zu organisieren:

Wir können die Schritte der Superpositionslösung in einer anderen Tabelle zusammenfassen. Wie wir bereits gesehen haben, müssen wir zum Ermitteln des komplexen Spitzenwerts einer Komponente den komplexen Spitzenwert der Anregungskomponente mit dem Wert der komplexen Übertragungsfunktion multiplizieren:

Und schließlich können wir die Zeitfunktion angeben, indem wir die komplexen Spitzenwerte der Komponenten kennen:

v_C(t) = 100 + 110 cos(w₀t - 56.3°) + 6.51 cos (3w₀t - 167.5°) V

Der Effektivwert (Effektivwert) der Spannung beträgt:

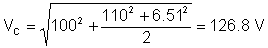
Wie Sie sehen, misst das Messgerät von TINA diesen Effektivwert.

Beispiel 2

Finden Sie die Zeitfunktion und den Effektivwert (Effektivwert) des Stroms i(t).

wenn R = 5 Ohm, C = 10 mF und v (t) = (100 + 200 cos (w₀t) + 30 cos (3w₀t - 90 °)) V wobei die Grundwinkelfrequenz ist w₀= 30 krad / s.

Versuchen Sie, das Problem mit dem Superpositionssatz zu lösen.

Die Lösungsschritte sind ähnlich wie in Beispiel 1, die Übertragungsfunktion ist jedoch unterschiedlich.

Ersetzen Sie nun die Zahlenwerte und s = jk w_0,wobei k = 0; 1; 3 in diesem Beispiel.

In V, A, Ohm, mF- und Mrad / s-Einheiten:

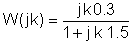
Es ist hilfreich, während der numerischen Lösung eine Tabelle zu verwenden:

Wir können die Schritte der Überlagerung in einer anderen Tabelle zusammenfassen. Wie wir bereits gesehen haben, sollten wir zum Ermitteln des Spitzenwerts einer Komponente den komplexen Spitzenwert dieser Anregungskomponente mit dem Wert der komplexen Übertragungsfunktion multiplizieren. Nutzen Sie die komplexen Spitzenwerte der Komponenten der Anregung:

Und schließlich können wir, wenn wir die komplexen Spitzenwerte der Komponenten kennen, die Zeitfunktion angeben:

i (t) = 32.4 cos (w₀t + 33.7°) + 5.85 cos (3w₀t - 77.5°) [EIN]

TDer Effektivwert des Stroms:

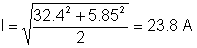
Sie können häufig einen Plausibilitätscheck für einen Teil der Lösung durchführen. Beispielsweise kann ein Kondensator eine Gleichspannung, aber keinen Gleichstrom haben.

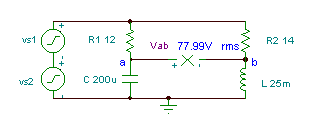
Beispiel 3

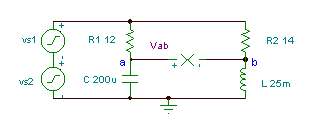
Ermitteln Sie die Zeitfunktion der Spannung V_ab if R₁= 12 Ohm, R₂ = 14 Ohm, L = 25 mH und

C = 200 mF. Die Generatorspannung beträgt v(t)=(50 + 80 cos(w₀t) + 30 cos (2 w₀t + 60 °)) V, wo die Grundfrequenz ist f₀ = 50 Hz.

Der erste Schritt besteht darin, die Übertragungsfunktion zu finden:

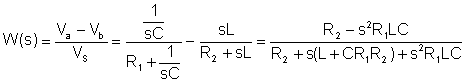
Ersetzen numerischer Werte in den Einheiten V, A, Ohm, mH, mF, kHz:

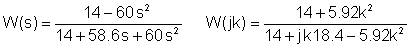
Zusammenführen der beiden Tabellen:

k V Sk		V abk
0 50		50
1 80		79.3 und-j66.3
2 30 ej60		29.7 und-j44.7

Zum Schluss noch die Zeitfunktion:

v_ab(t) = 50 + 79.3 cos (w₁t - 66.3°) + 29.7 cos (2w₁t - 44.7°) [V]

und der Effektivwert:

---