Klicken Sie auf oder tippen Sie auf die Beispielschaltkreise, um TINACloud aufzurufen und den interaktiven Gleichstrommodus auszuwählen, um sie online zu analysieren. Erhalten Sie einen kostengünstigen Zugang zu TINACloud, um die Beispiele zu bearbeiten oder eigene Schaltungen zu erstellen
Zwei Induktoren oder Spulen, die durch elektromagnetische Induktion verbunden sind, werden als gekoppelte Induktoren bezeichnet. Wenn ein Wechselstrom durch eine Spule fließt, baut die Spule ein Magnetfeld auf, das mit der zweiten Spule gekoppelt ist und eine Spannung in dieser Spule induziert. Das Phänomen, dass ein Induktor eine Spannung in einem anderen Induktor induziert, ist bekannt als Gegeninduktivität.
Gekoppelte Spulen können als Grundmodell für Transformatoren verwendet werden, ein wichtiger Bestandteil von Stromverteilungssystemen und elektronischen Schaltkreisen. Transformatoren werden zum Ändern von Wechselspannungen, Strömen und Impedanzen sowie zum Trennen eines Teils eines Stromkreises von einem anderen verwendet.
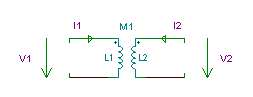
Drei Parameter sind erforderlich, um ein Paar gekoppelter Induktivitäten zu charakterisieren: zwei Selbstinduktivitäten, L1 und ich2und der gegenseitige Induktivität, L12 = M. Das Symbol für gekoppelte Induktivitäten lautet:
Schaltungen, die gekoppelte Induktivitäten enthalten, sind komplizierter als andere Schaltungen, da wir die Spannung der Spulen nur in Form ihrer Ströme ausdrücken können. Die folgenden Gleichungen gelten für die obige Schaltung mit den Punktpositionen und Referenzrichtungen gezeigt:
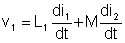
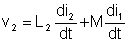
Verwenden Sie stattdessen Impedanzen:
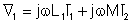
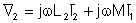
Die gegenseitigen Induktivitätsterme können ein negatives Vorzeichen haben, wenn die Punkte unterschiedliche Positionen haben. Die maßgebliche Regel ist, dass die induzierte Spannung an einer gekoppelten Spule relativ zu ihrem Punkt die gleiche Richtung hat wie der induzierende Strom zu seinem eigenen Punkt auf dem gekoppelten Gegenstück.
Das T - Äquivalent Schaltung
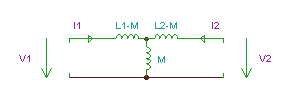
ist sehr nützlich beim Lösen Schaltungen mit gekoppelten Spulen.
Wenn Sie die Gleichungen schreiben, können Sie die Äquivalenz leicht überprüfen.
Lassen Sie uns dies anhand einiger Beispiele veranschaulichen.
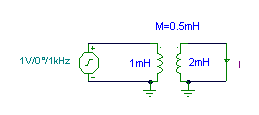
Beispiel 1
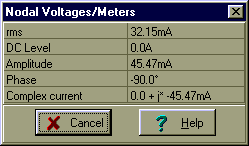
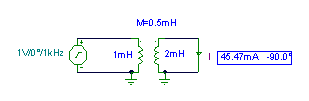
Finden Sie die Amplitude und den anfänglichen Phasenwinkel des Stroms.
vs (t) = 1cos (w ×Fernseher w= 1kHz
Die Gleichungen: VS = Ich1*j w L1 - I * j w M
0 = I * j w L2 - Ich1*j w M
Daher: ich1 = I * L2/ M; und
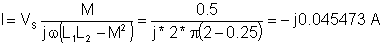
i (t) = 0.045473 cos (w ×t - 90°) A
om: = 2 * pi * 1000;
Sys I1, I
1 = I1 * j * om * 0.001-I * j * om * 0.0005
0 = I * j * om * 0.002-I1 * j * om * 0.0005
end;
abs (I) = [45.4728m]
Radtodeg (Bogen (I)) = [- 90]
Importiere Mathe als m, cmath als c, Numpy als n
#Vereinfachen wir den Ausdruck von Komplexen
#Zahlen für mehr Transparenz:
cp= lambda Z : „{:.4f}“.format(Z)
om=2000*c.pi
#Wir haben ein lineares System
#von Gleichungen, die
#wir wollen nach I1 auflösen, I:
#1=I1*j*om*0.001-I*j*om*0.0005
#0=I*j*om*0.002-I1*j*om*0.0005
#Schreiben Sie die Matrix der Koeffizienten auf:
A=n.array([[1j*om*0.001,-1j*om*0.0005],
[-1j*om*0.0005,1j*om*0.002]])
#Schreiben Sie die Matrix der Konstanten auf:
b=n.array([1,0])
I1,I= n.linalg.solve(A,b)
print(“abs(I)=",cp(abs(I)))
print(“phase(I)=",n.degrees(c.phase(I)))
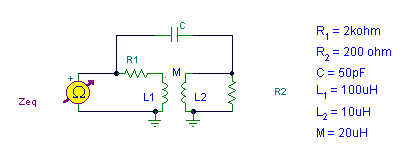
Beispiel 2
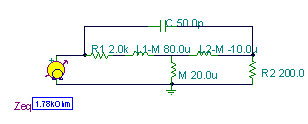
Finden Sie die äquivalente Impedanz des zweipoligen bei 2 MHz!
Zuerst zeigen wir die Lösung, die durch Lösen der Schleifengleichungen erhalten wird. Wir nehmen an, dass der Impedanzmesserstrom 1 A beträgt, so dass die Messspannung der Impedanz entspricht. Sie können die Lösung im Interpreter von TINA sehen.
{Schleifengleichungen verwenden}
L1: = 0.0001;
L2: = 0.00001;
M: = 0.00002;
om: = 2 * pi * 2000000;
Sys Vs, J1, J2, J3
J1*(R1+j*om*L1)+J2*j*om*M-Vs=0
J1 + J3 = 1
J2*(R2+j*om*L2)+J1*om*j*M-J3*R2=0
J3*(R2+1/j/om/C)-J2*R2-Vs=0
end;
Z: = Vs;
Z = [1.2996k-1.1423k * j]
Mathe als m importieren
cmath als c importieren
#Vereinfachen wir den Ausdruck von Komplexen
#Zahlen für mehr Transparenz:
cp= lambda Z : „{:.4f}“.format(Z)
#Verwenden Sie Schleifengleichungen
L1=0.0001
L2=0.00006
M = 0.00002
om=4000000*c.pi
#Wir haben ein lineares Gleichungssystem
#das wir nach Vs,J1,J2,J3 auflösen wollen:
#J1*(R1+j*om*L1)+J2*j*om*M-Vs=0
#J1+J3=1
#J2*(R2+j*om*L2)+J1*om*j*M-J3*R2=0
#J3*(R2+1/j/om/C)-J2*R2-Vs=0
numpy als n importieren
#Schreiben Sie die Matrix der Koeffizienten auf:
A=n.array([[-1,R1+1j*om*L1,1j*om*M,0],
[0,1,0,1]
[0,om*1j*M,R2+1j*om*L2,-R2],
[-1,0,-R2,R2+1/1j/om/C]])
#Schreiben Sie die Matrix der Konstanten auf:
b=n.array([0,1,0,0])
Vs,J1,J2,J3=n.linalg.solve(A,b)
Z=Vs
print(“Z=",cp(Z))
print(“abs(Z)=",cp(abs(Z)))
Wir könnten dieses Problem auch mit dem T-Äquivalent des Transformators in TINA lösen:
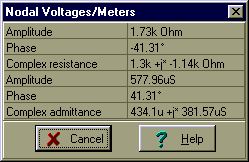
Wenn wir die äquivalente Impedanz von Hand berechnen wollten, müssten wir die Stern-Dreieck-Umwandlung verwenden. Während dies hier möglich ist, können Schaltungen im Allgemeinen sehr kompliziert sein, und es ist bequemer, die Gleichungen für gekoppelte Spulen zu verwenden.
English
English
German
French
Spanish
Portuguese
Russian
Chinese (Simplified)
Chinese (Traditional)
Japanese
Korean
Hungarian