Klicken Sie auf oder tippen Sie auf die Beispielschaltkreise, um TINACloud aufzurufen und den interaktiven Gleichstrommodus auszuwählen, um sie online zu analysieren.
Klicken Sie auf oder tippen Sie auf die Beispielschaltkreise, um TINACloud aufzurufen und den interaktiven Gleichstrommodus auszuwählen, um sie online zu analysieren.
Erhalten Sie einen kostengünstigen Zugang zu TINACloud, um die Beispiele zu bearbeiten oder eigene Schaltungen zu erstellen
Wir haben bereits gezeigt, wie die elementaren Methoden der Gleichstromkreisanalyse erweitert und in Wechselstromkreisen verwendet werden können, um die komplexen Spitzen- oder Effektivwerte von Spannung und Strom sowie die komplexe Impedanz oder Admittanz zu ermitteln. In diesem Kapitel werden wir einige Beispiele für die Spannungs- und Stromaufteilung in Wechselstromkreisen lösen.
Beispiel 1
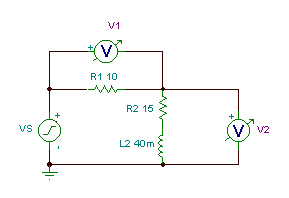
Finden Sie die Spannungen v1(t) und v2(t) vorausgesetzt, dass vs(T)= 110cos (2p50t).
Lassen Sie uns dieses Ergebnis zunächst durch manuelle Berechnung mithilfe der Spannungsteilungsformel erhalten.
Das Problem kann als zwei komplexe Impedanzen in Reihe betrachtet werden: die Impedanz des Widerstands R1, Z1=R1 Ohm (was eine reelle Zahl ist) und die äquivalente Impedanz von R2 und ich2 in Serie, Z2 = R2 + j w L2.
Durch Ersetzen der äquivalenten Impedanzen kann die Schaltung in TINA wie folgt neu gezeichnet werden:
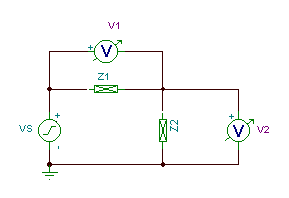
Beachten Sie, dass wir eine neue Komponente verwendet haben, eine komplexe Impedanz, die jetzt in TINA v6 verfügbar ist. Die Frequenzabhängigkeit von Z können Sie über eine Tabelle definieren, die Sie durch Doppelklick auf die Impedanzkomponente erreichen. In der ersten Zeile der Tabelle können Sie entweder die Gleichstromimpedanz oder eine frequenzunabhängige komplexe Impedanz definieren (letzteres haben wir hier für die Induktivität und den Widerstand in Reihe bei der angegebenen Frequenz durchgeführt).
Mit der Formel zur Spannungsteilung:
V1 = Vs*Z1 / (Z1 + Z2)
V2 = Vs*Z2 / (Z1 + Z2)
Numerisch:
Z1 = R1 = 10 Ohm
Z2 = R2 + j w L = 15 + j 2*p* 50*0.04 =15 + j 12.56 Ohm
V1= 110*10/ (25+j12.56) = 35.13-j17.65 V = 39.31 e -j26.7 ° V
V2= 110*(15+j12.56) / (25 +j12.56) = 74.86 +j17.65 V = 76.92 e j 13.3° V
Die Zeitfunktion der Spannungen:
v1(t) = 39.31 cos (wt – 26.7°) V
v2(t) = 76.9 cos (wt + 13.3°) V
Lassen Sie uns das Ergebnis mit TINA überprüfen Analyse/AC-Analyse/Knoten berechnen SpannungenV1
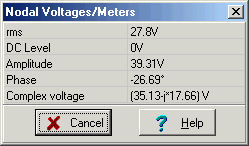
V2
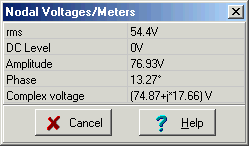
Als nächstes überprüfen wir diese Ergebnisse mit TINAs Interpreter:
f: = 50;
om: = 2 * pi * f;
VS: = 110;
v1:=VS*R1/(R1+R2+j*om*L2);
v2:=VS*(R2+j*om*L2)/(R1+R2+j*om*L2);
v1 = [35.1252-17.6559 * j]
v2 = [74.8748 + 17.6559 * j]
abs (v2) = [76.9283]
radtodeg (arc (v2)) = [13.2683]
abs (v1) = [39.313]
radtodeg (arc (v1)) = [- 26.6866]
Mathe als m importieren
cmath als c importieren
#Vereinfachen wir den Ausdruck von Komplexen
#Zahlen für mehr Transparenz:
cp= lambda Z : „{:.4f}“.format(Z)
f = 50
om=2*c.pi*f
VS=110
v1=VS*R1/complex(R1+R2,om*L2)
v2=VS*complex(R2,om*L2)/complex(R1+R2,om*L2)
print(“v1=",cp(v1))
print(“v2=",cp(v2))
print(“abs(v1)= %.4f”%abs(v1))
print(“degrees(arc(v1))= %.4f”%m.degrees(c.phase(v1)))
print(“abs(v2)= %.4f”%abs(v2))
print(“arc(v2)*180/pi= %.4f”%(c.phase(v2)*180/c.pi))
Beachten Sie, dass wir bei Verwendung des Interpreters die Werte der passiven Komponenten nicht deklarieren mussten. Dies liegt daran, dass wir den Interpreter in einer Arbeitssitzung mit TINA verwenden, in der sich der Schaltplan im Schaltplaneditor befindet. TINAs Interpreter sucht in diesem Schema nach der Definition der passiven Komponentensymbole, die in das Interpreter-Programm eingegeben werden.
Lassen Sie uns abschließend das Zeigerdiagramm von TINA verwenden, um dieses Ergebnis zu demonstrieren. Anschließen eines Voltmeters an den Spannungsgenerator, Auswahl der Analyse/AC-Analyse/Zeigerdiagramm Wenn Sie den Befehl ausführen, die Achsen festlegen und die Beschriftungen hinzufügen, erhalten Sie das folgende Diagramm. Beachten Sie, dass Ansicht / Vektorbeschriftungsstil wurde auf Amplitude für dieses Diagramm.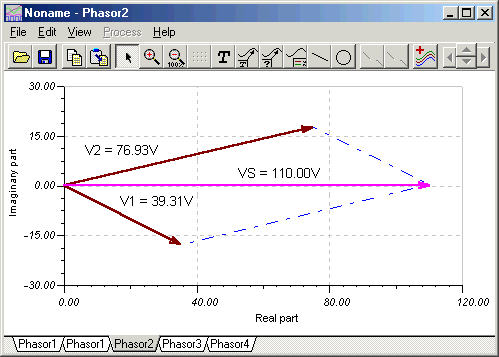
Das Diagramm zeigt das Vs ist die Summe der Zeiger V1 und V2, Vs = V1 + V2.
Durch Verschieben der Zeiger können wir das auch zeigen V2 ist der Unterschied zwischen Vs und V1, V2 = Vs - V1.
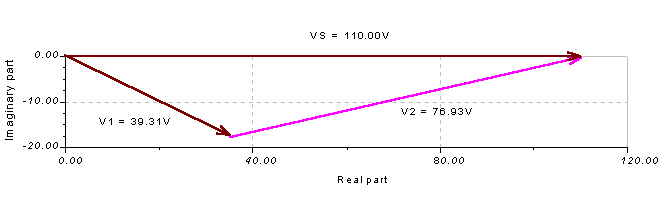
Diese Abbildung zeigt auch die Subtraktion von Vektoren. Der resultierende Vektor sollte an der Spitze des zweiten Vektors beginnen. V1.
Auf ähnliche Weise können wir das zeigen V1 = Vs - V2. Der resultierende Vektor sollte wieder von der Spitze des zweiten Vektors ausgehen. V1.
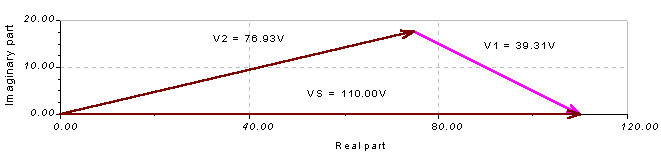
Natürlich können beide Zeigerdiagramme als einfache Dreiecksregeldiagramme betrachtet werden Vs = V1 + V2 .
Die obigen Zeigerdiagramme veranschaulichen auch das Kirchhoffsche Spannungsgesetz (KVL).
Wie wir in unserer Untersuchung von Gleichstromkreisen erfahren haben, entspricht die angelegte Spannung einer Reihenschaltung der Summe der Spannungsabfälle an den Reihenelementen. Die Zeigerdiagramme zeigen, dass KVL auch für Wechselstromkreise gilt. aber nur, wenn wir komplexe Zeiger verwenden!
Beispiel 2
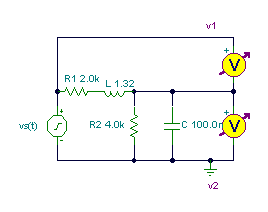
In dieser Schaltung hat R1 stellt den Gleichstromwiderstand der Spule L dar; Gemeinsam modellieren sie einen realen Induktor mit seiner Verlustkomponente. Finden Sie die Spannung am Kondensator und die Spannung an der realen Spule.
L = 1.32 h, R1 = 2 kOhm, R2 = 4 kOhm, C = 0.1 mF, vS(t) = 20 cos (wt) V, f = 300Hz.
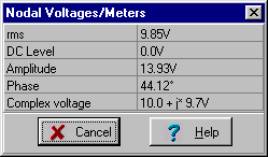
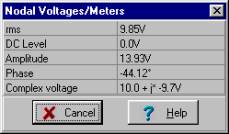
Manuelles Lösen mittels Spannungsteilung:
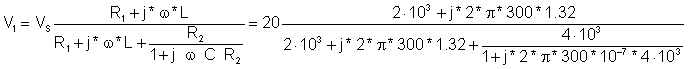
= 13.91 e j 44.1° V
und
v1(t) = 13.9 cos (w ×t + 44°) V
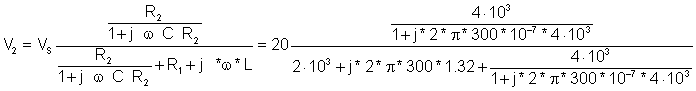
= 13.93 e -j 44.1° V
und
v2(t) = 13.9 cos(w ×t – 44.1°) V
Beachten Sie, dass bei dieser Frequenz und diesen Komponentenwerten die Größen der beiden Spannungen nahezu gleich sind, die Phasen jedoch entgegengesetzte Vorzeichen haben.
Lassen Sie uns noch einmal TINA die mühsame Arbeit erledigen lassen, indem wir nach V1 und V2 auflösen mit dem Dolmetscher:
om: = 600 * pi;
V: = 20;
v1:=V*(R1+j*om*L)/(R1+j*om*L+replus(R2,(1/j/om/C)));
abs (v1) = [13.9301]
180 * Bogen (v1) / pi = [44.1229]
v2:=V*(replus(R2,1/j/om/C))/(R1+j*om*L+replus(R2,(1/j/om/C)));
abs (v2) = [13.9305]
180 * Bogen (v2) / pi = [- 44.1211]
Mathe als m importieren
cmath als c importieren
#Vereinfachen wir den Ausdruck von Komplexen
#Zahlen für mehr Transparenz:
cp= lambda Z : „{:.4f}“.format(Z)
#Replus mit Lambda definieren:
Replus= Lambda R1, R2 : R1*R2/(R1+R2)
om=600*c.pi
V = 20
v1=V*complex(R1,om*L)/complex(R1+1j*om*L+Replus(R2,1/1j/om/C))
print(“abs(v1)= %.4f”%abs(v1))
print(“180*arc(v1)/pi= %.4f”%(180*c.phase(v1)/c.pi))
v2=V*complex(Replus(R2,1/1j/om/C))/complex(R1+1j*om*L+Replus(R2,1/1j/om/C))
print(“abs(v2)= %.4f”%abs(v2))
print(“180*arc(v2)/pi= %.4f”%(180*c.phase(v2)/c.pi))
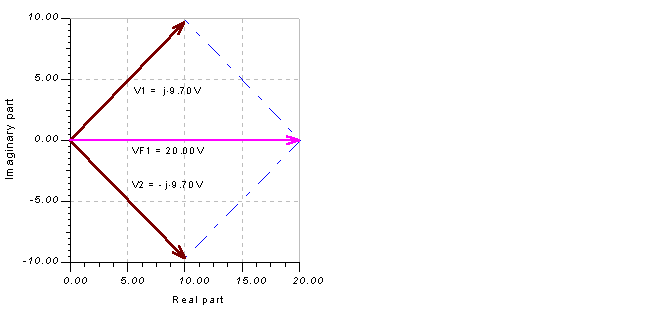
Und schließlich sehen Sie sich dieses Ergebnis anhand des Zeigerdiagramms von TINA an. Anschließen eines Voltmeters an den Spannungsgenerator, Aufrufen des Analyse/AC-Analyse/Zeigerdiagramm Befehl, Festlegen der Achsen und Hinzufügen der Beschriftungen ergeben das folgende Diagramm (beachten Sie, dass wir festgelegt haben Ansicht / Vektorbeschriftungsstil zu Real + j * Imag für dieses Diagramm):
Beispiel 3
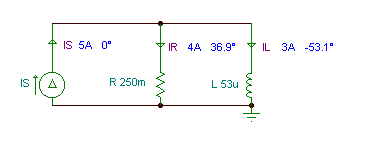
Die aktuelle Quelle iS(t) = 5 cos (wt) A, der Widerstand R = 250 Mohm, die Induktivität L = 53 uH und die Frequenz f = 1 kHz. Ermitteln Sie den Strom in der Induktivität und den Strom im Widerstand.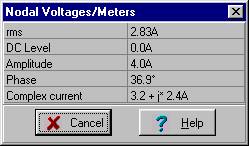

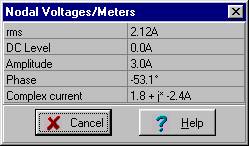

Verwendung der Formel für die aktuelle Division:
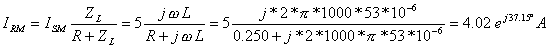
iR(t) = 4 cos (w ×t + 37.2°) EIN
Ähnlich:

iL(t) = 3 cos(w ×t – 53.1°)
Und mit dem Dolmetscher in TINA:
om: = 2 * pi * 1000;
ist: = 5;
iL: = ist * R / (R + j * om * L);
iL = [1.8022-2.4007 * j]
iR: = ist * j * om * L / (R + j * om * L);
iR = [3.1978 + 2.4007 * j]
abs (iL) = [3.0019]
Radtodeg (Bogen (iL)) = [- 53.1033]
abs (iR) = [3.9986]
Radtodeg (Bogen (iR)) = [36.8967]
Mathe als m importieren
cmath als c importieren
#Vereinfachen wir den Ausdruck von Komplexen
#Zahlen für mehr Transparenz:
cp= lambda Z : „{:.4f}“.format(Z)
om=2*c.pi*1000
i = 5
iL=i*R/komplex(R+1j*om*L)
print(“iL=",cp(iL))
iR=complex(i*1j*om*L/(R+1j*om*L))
print(“iR=",cp(iR))
print(“abs(iL)= %.4f”%abs(iL))
print(“degrees(arc(iL))= %.4f”%m.degrees(c.phase(iL)))
print(“abs(iR)= %.4f”%abs(iR))
print(“degrees(arc(iR))= %.4f”%m.degrees(c.phase(iR)))
Wir können diese Lösung auch mit einem Zeigerdiagramm demonstrieren:
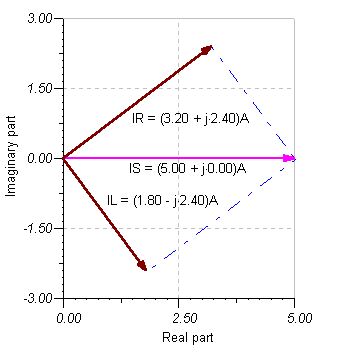
Das Zeigerdiagramm zeigt, dass der Generatorstrom IS der resultierende Vektor der komplexen Ströme IL und IR ist. Es zeigt auch das Kirchhoffsche Stromgesetz (KCL) und zeigt, dass der Strom, der in den oberen Knoten der Schaltung eintritt, gleich der Summe von IL und IR ist, wobei die komplexen Ströme den Knoten verlassen.
Beispiel 4
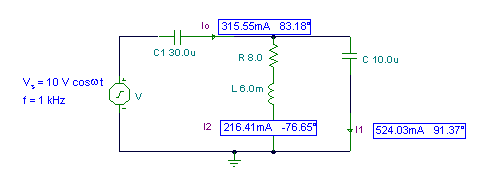
Bestimmen Sie i0(t), i1(t) und ich2(T). Die Komponentenwerte sowie die Quellenspannung, -frequenz und -phase sind im Diagramm unten angegeben.
i0
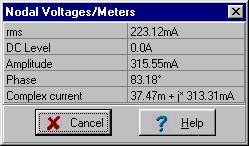
i1
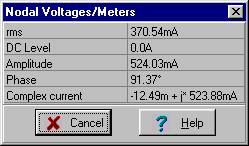
i2
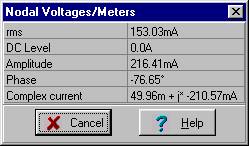
In unserer Lösung verwenden wir das Prinzip der Stromteilung. Zuerst finden wir den Ausdruck für den Gesamtstrom i0:
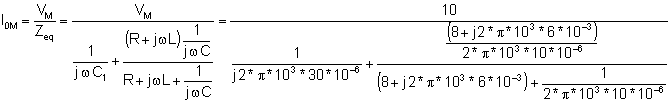
I0M = 0.315 e j 83.2° A und i0(t) = 0.315 cos (w ×t + 83.2°) EIN
Dann ermitteln wir mit der Stromteilung den Strom im Kondensator C:
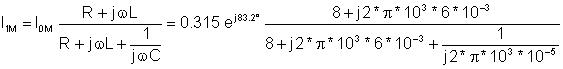
I1M = 0.524 e j 91.4° A und i1(t) = 0.524 cos (w ×t + 91.4°) EIN
Und der Strom in der Induktivität:
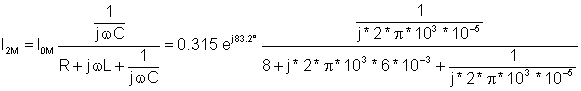
I2M = 0.216 e-j 76.6° A und i2(t) = 0.216 cos(w ×t – 76.6°) EIN
Voller Vorfreude suchen wir nach einer Bestätigung unserer Handberechnungen mit TINAs Interpreter.
V: = 10;
om: = 2 * pi * 1000;
I0: = V / ((1 / j / om / C1) + Replus ((1 / j / om / C), (R + j * om * L));
I0 = [37.4671m + 313.3141m * j]
abs (I0) = [315.5463m]
180 * arc (I0) / pi = [83.1808]
I1: = I0 * (R + j * om * L) / (R + j * om * L + 1 / j / om / C);
I1 = [- 12.489m + 523.8805m * j]
abs (I1) = [524.0294m]
180 * arc (I1) / pi = [91.3656]
I2: = I0 * (1 / j / om / C) / (R + j * om * L + 1 / j / om / C);
I2 = [49.9561m-210.5665m * j]
abs (I2) = [216.4113m]
180 * arc (I2) / pi = [- 76.6535]
{Kontrolle: I1 + I2 = I0}
abs (I1 + I2) = [315.5463m]
Mathe als m importieren
cmath als c importieren
#Vereinfachen wir den Ausdruck von Komplexen
#Zahlen für mehr Transparenz:
cp= lambda Z : „{:.4f}“.format(Z)
#Definieren Sie zuerst Replus mit Lambda:
Replus= Lambda R1, R2 : R1*R2/(R1+R2)
V = 10
om=2*c.pi*1000
I0=V/complex((1/1j/om/C1)+Replus(1/1j/om/C,R+1j*om*L))
print(“I0=",cp(I0))
print(“abs(I0)= %.4f”%abs(I0))
print(“180*arc(I0)/pi= %.4f”%(180*c.phase(I0)/c.pi))
I1=I0*complex(R,om*L)/complex(R+1j*om*L+1/1j/om/C)
print(“I1=",cp(I1))
print(“abs(I1)= %.4f”%abs(I1))
print(“180*arc(I1)/pi= %.4f”%(180*c.phase(I1)/c.pi))
I2=I0*complex(1/1j/om/C)/complex(R+1j*om*L+1/1j/om/C)
print(“I2=",cp(I2))
print(“abs(I2)= %.4f”%abs(I2))
print(“180*arc(I2)/pi= %.4f”%(180*c.phase(I2)/c.pi))
#Steuerung: I1+I2=I0
print(“abs(I1+I2)= %.4f”%abs(I1+I2))
Eine andere Möglichkeit, dieses Problem zu lösen, wäre, zunächst die Spannung an der parallelen komplexen Impedanz von Z zu ermittelnLR und ZC. Wenn wir diese Spannung kennen, könnten wir die Ströme i ermitteln1 und ich2 indem man diese Spannung dann zunächst durch Z dividiertLR und dann um ZC. Als nächstes zeigen wir die Lösung für die Spannung an der parallelen komplexen Impedanz von ZLR und ZC. Auf dem Weg müssen wir das Prinzip der Spannungsteilung verwenden:
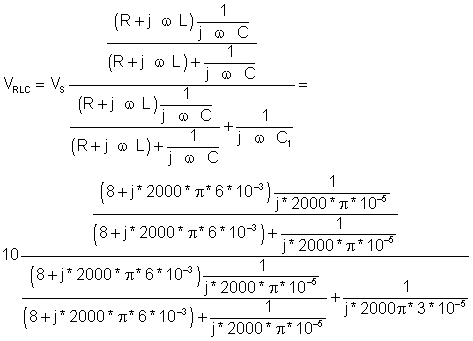
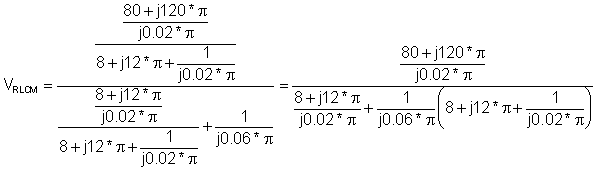
VRLCM = 8.34 e j 1.42° V
und
IC = I1= VRLCM*jwC = 0.524 e j 91.42° A
und daher
iC (t) = 0.524 cos (w ×t + 91.4°) EIN.